Learning physical unknowns from hydrodynamic shock and material interface features in ICF capsule implosions

In high energy density physics (HEDP) and inertial confinement fusion (ICF), predictive modeling is complicated by uncertainty in parameters that characterize various aspects of the modeled system, such as those characterizing material properties, equation of state (EOS), opacities, and initial conditions. Typically, however, these parameters are not directly observable. What is observed instead is a time sequence of radiographic projections using X-rays. In this work, we define a set of sparse hydrodynamic features derived from the outgoing shock profile and outer material edge, which can be obtained from radiographic measurements, to directly infer such parameters. Our machine learning (ML)-based methodology involves a pipeline of two architectures, a radiograph-to-features network (R2FNet) and a features-to-parameters network (F2PNet), that are trained independently and later combined to approximate a posterior distribution for the parameters from radiographs. We show that the estimated parameters can be used in a hydrodynamics code to obtain density fields and hydrodynamic shock and outer edge features that are consistent with the data. Finally, we demonstrate that features resulting from an unknown EOS model can be successfully mapped onto parameters of a chosen analytical EOS model, implying that network predictions are learning physics, with a degree of invariance to the underlying choice of EOS model.

Learning Robust Features for Scatter Removal and Reconstruction in Dynamic ICF X-Ray Tomography

Density reconstruction from X-ray projections is an important problem in radiography with key applications in scientific and industrial X-ray computed tomography (CT). Often, such projections are corrupted by unknown sources of noise and scatter, which when not properly accounted for, can lead to significant errors in density reconstruction. In the setting of this problem, recent deep learning-based methods have shown promise in improving the accuracy of density reconstruction. In this article, we propose a deep learning-based encoder-decoder framework wherein the encoder extracts robust features from noisy/corrupted X-ray projections and the decoder reconstructs the density field from the features extracted by the encoder. We explore three options for the latent-space representation of features: physics-inspired supervision, self-supervision, and no supervision. We find that variants based on self-supervised and physicsinspired supervised features perform better over a range of unknown scatter and noise. In extreme noise settings, the variant with self-supervised features performs best. After investigating further details of the proposed deep-learning methods, we conclude by demonstrating that the newly proposed methods are able to achieve higher accuracy in density reconstruction when compared to a traditional iterative technique.

Reconstructing Richtmyer-Meshkov instabilities from noisy radiographs using low dimensional features and attention-based neural networks

A trained attention-based transformer network can robustly recover the complex topologies given by the Richtmyer-Meshkoff instability from a sequence of hydrodynamic features derived from radiographic images corrupted with blur, scatter, and noise. This approach is demonstrated on ICF-like double shell hydrodynamic simulations. The key component of this network is a transformer encoder that acts on a sequence of features extracted from noisy radiographs. This encoder includes numerous self-attention layers that act to learn temporal dependencies in the input sequences and increase the expressiveness of the model. This approach is demonstrated to exhibit an excellent ability to accurately recover the Richtmyer-Meshkov instability growth rates, even despite the gas-metal interface being greatly obscured by radiographic noise.

High-Precision Inversion of Dynamic Radiography Using Hydrodynamic Features

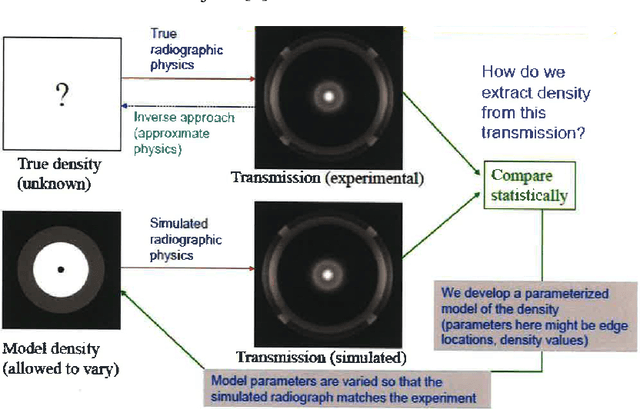
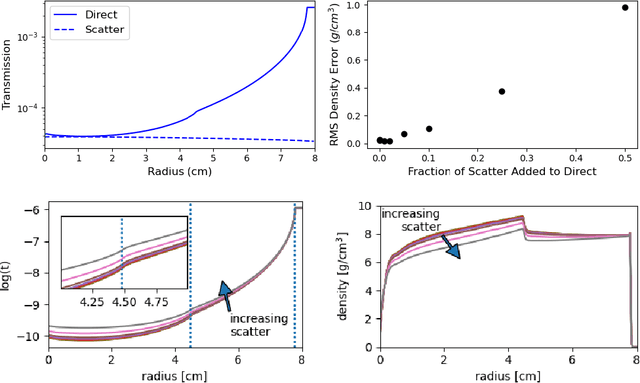
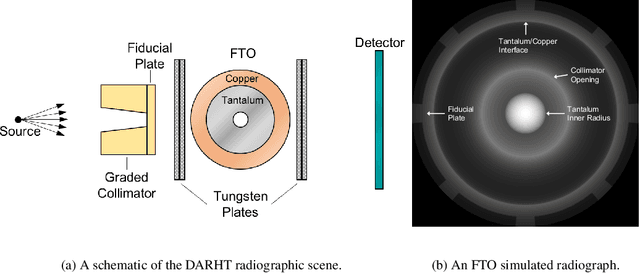
Radiography is often used to probe complex, evolving density fields in dynamic systems and in so doing gain insight into the underlying physics. This technique has been used in numerous fields including materials science, shock physics, inertial confinement fusion, and other national security applications. In many of these applications, however, complications resulting from noise, scatter, complex beam dynamics, etc. prevent the reconstruction of density from being accurate enough to identify the underlying physics with sufficient confidence. As such, density reconstruction from static/dynamic radiography has typically been limited to identifying discontinuous features such as cracks and voids in a number of these applications. In this work, we propose a fundamentally new approach to reconstructing density from a temporal sequence of radiographic images. Using only the robust features identifiable in radiographs, we combine them with the underlying hydrodynamic equations of motion using a machine learning approach, namely, conditional generative adversarial networks (cGAN), to determine the density fields from a dynamic sequence of radiographs. Next, we seek to further enhance the hydrodynamic consistency of the ML-based density reconstruction through a process of parameter estimation and projection onto a hydrodynamic manifold. In this context, we note that the distance from the hydrodynamic manifold given by the training data to the test data in the parameter space considered both serves as a diagnostic of the robustness of the predictions and serves to augment the training database, with the expectation that the latter will further reduce future density reconstruction errors. Finally, we demonstrate the ability of this method to outperform a traditional radiographic reconstruction in capturing allowable hydrodynamic paths even when relatively small amounts of scatter are present.

Physics-Driven Learning of Wasserstein GAN for Density Reconstruction in Dynamic Tomography

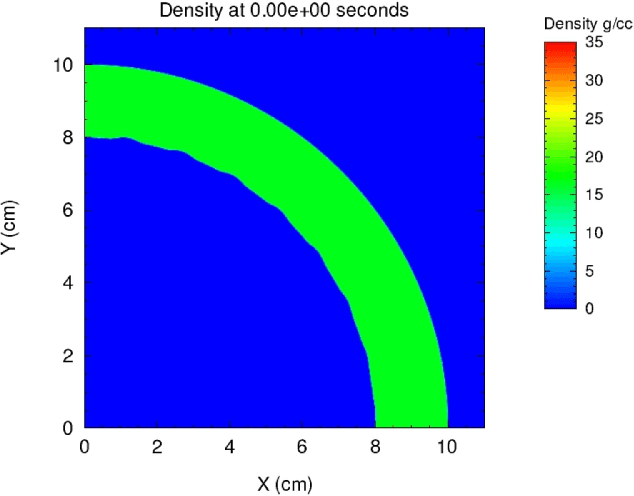
Object density reconstruction from projections containing scattered radiation and noise is of critical importance in many applications. Existing scatter correction and density reconstruction methods may not provide the high accuracy needed in many applications and can break down in the presence of unmodeled or anomalous scatter and other experimental artifacts. Incorporating machine-learned models could prove beneficial for accurate density reconstruction particularly in dynamic imaging, where the time-evolution of the density fields could be captured by partial differential equations or by learning from hydrodynamics simulations. In this work, we demonstrate the ability of learned deep neural networks to perform artifact removal in noisy density reconstructions, where the noise is imperfectly characterized. We use a Wasserstein generative adversarial network (WGAN), where the generator serves as a denoiser that removes artifacts in densities obtained from traditional reconstruction algorithms. We train the networks from large density time-series datasets, with noise simulated according to parametric random distributions that may mimic noise in experiments. The WGAN is trained with noisy density frames as generator inputs, to match the generator outputs to the distribution of clean densities (time-series) from simulations. A supervised loss is also included in the training, which leads to improved density restoration performance. In addition, we employ physics-based constraints such as mass conservation during network training and application to further enable highly accurate density reconstructions. Our preliminary numerical results show that the models trained in our frameworks can remove significant portions of unknown noise in density time-series data.