Reconstructing Richtmyer-Meshkov instabilities from noisy radiographs using low dimensional features and attention-based neural networks

A trained attention-based transformer network can robustly recover the complex topologies given by the Richtmyer-Meshkoff instability from a sequence of hydrodynamic features derived from radiographic images corrupted with blur, scatter, and noise. This approach is demonstrated on ICF-like double shell hydrodynamic simulations. The key component of this network is a transformer encoder that acts on a sequence of features extracted from noisy radiographs. This encoder includes numerous self-attention layers that act to learn temporal dependencies in the input sequences and increase the expressiveness of the model. This approach is demonstrated to exhibit an excellent ability to accurately recover the Richtmyer-Meshkov instability growth rates, even despite the gas-metal interface being greatly obscured by radiographic noise.

Shorter SPECT Scans Using Self-supervised Coordinate Learning to Synthesize Skipped Projection Views

Purpose: This study addresses the challenge of extended SPECT imaging duration under low-count conditions, as encountered in Lu-177 SPECT imaging, by developing a self-supervised learning approach to synthesize skipped SPECT projection views, thus shortening scan times in clinical settings. Methods: We employed a self-supervised coordinate-based learning technique, adapting the neural radiance field (NeRF) concept in computer vision to synthesize under-sampled SPECT projection views. For each single scan, we used self-supervised coordinate learning to estimate skipped SPECT projection views. The method was tested with various down-sampling factors (DFs=2, 4, 8) on both Lu-177 phantom SPECT/CT measurements and clinical SPECT/CT datasets, from 11 patients undergoing Lu-177 DOTATATE and 6 patients undergoing Lu-177 PSMA-617 radiopharmaceutical therapy. Results: For SPECT reconstructions, our method outperformed the use of linearly interpolated projections and partial projection views in relative contrast-to-noise-ratios (RCNR) averaged across different downsampling factors: 1) DOTATATE: 83% vs. 65% vs. 67% for lesions and 86% vs. 70% vs. 67% for kidney, 2) PSMA: 76% vs. 69% vs. 68% for lesions and 75% vs. 55% vs. 66% for organs, including kidneys, lacrimal glands, parotid glands, and submandibular glands. Conclusion: The proposed method enables reduction in acquisition time (by factors of 2, 4, or 8) while maintaining quantitative accuracy in clinical SPECT protocols by allowing for the collection of fewer projections. Importantly, the self-supervised nature of this NeRF-based approach eliminates the need for extensive training data, instead learning from each patient's projection data alone. The reduction in acquisition time is particularly relevant for imaging under low-count conditions and for protocols that require multiple-bed positions such as whole-body imaging.

Learning Image Priors through Patch-based Diffusion Models for Solving Inverse Problems

Diffusion models can learn strong image priors from underlying data distribution and use them to solve inverse problems, but the training process is computationally expensive and requires lots of data. Such bottlenecks prevent most existing works from being feasible for high-dimensional and high-resolution data such as 3D images. This paper proposes a method to learn an efficient data prior for the entire image by training diffusion models only on patches of images. Specifically, we propose a patch-based position-aware diffusion inverse solver, called PaDIS, where we obtain the score function of the whole image through scores of patches and their positional encoding and utilize this as the prior for solving inverse problems. First of all, we show that this diffusion model achieves an improved memory efficiency and data efficiency while still maintaining the capability to generate entire images via positional encoding. Additionally, the proposed PaDIS model is highly flexible and can be plugged in with different diffusion inverse solvers (DIS). We demonstrate that the proposed PaDIS approach enables solving various inverse problems in both natural and medical image domains, including CT reconstruction, deblurring, and superresolution, given only patch-based priors. Notably, PaDIS outperforms previous DIS methods trained on entire image priors in the case of limited training data, demonstrating the data efficiency of our proposed approach by learning patch-based prior.

Provable Preconditioned Plug-and-Play Approach for Compressed Sensing MRI Reconstruction

Model-based methods play a key role in the reconstruction of compressed sensing (CS) MRI. Finding an effective prior to describe the statistical distribution of the image family of interest is crucial for model-based methods. Plug-and-play (PnP) is a general framework that uses denoising algorithms as the prior or regularizer. Recent work showed that PnP methods with denoisers based on pretrained convolutional neural networks outperform other classical regularizers in CS MRI reconstruction. However, the numerical solvers for PnP can be slow for CS MRI reconstruction. This paper proposes a preconditioned PnP (P^2nP) method to accelerate the convergence speed. Moreover, we provide proofs of the fixed-point convergence of the P^2nP iterates. Numerical experiments on CS MRI reconstruction with non-Cartesian sampling trajectories illustrate the effectiveness and efficiency of the P^2nP approach.

AWFSD: Accelerated Wirtinger Flow with Score-based Diffusion Image Prior for Poisson-Gaussian Holographic Phase Retrieval

Phase retrieval (PR) is an essential problem in a number of coherent imaging systems. This work aims at resolving the holographic phase retrieval problem in real world scenarios where the measurements are corrupted by a mixture of Poisson and Gaussian (PG) noise that stems from optical imaging systems. To solve this problem, we develop a novel algorithm based on Accelerated Wirtinger Flow that uses Score-based Diffusion models as the generative prior (AWFSD). In particular, we frame the PR problem as an optimization task that involves both a data fidelity term and a regularization term. We derive the gradient of the PG log-likelihood function along with its corresponding Lipschitz constant, ensuring a more accurate data consistency term for practical measurements. We introduce a generative prior as part of our regularization approach by using a score-based diffusion model to capture (the gradient of) the image prior distribution. We provide theoretical analysis that establishes a critical-point convergence guarantee for the proposed AWFSD algorithm. Our simulation experiments demonstrate that: 1) The proposed algorithm based on the PG likelihood model enhances reconstruction compared to that solely based on either Gaussian or Poisson likelihood. 2) The proposed AWFSD algorithm produces reconstructions with higher image quality both qualitatively and quantitatively, and is more robust to variations in noise levels when compared with state-of-the-art methods for phase retrieval.

CoRRECT: A Deep Unfolding Framework for Motion-Corrected Quantitative R2* Mapping

Quantitative MRI (qMRI) refers to a class of MRI methods for quantifying the spatial distribution of biological tissue parameters. Traditional qMRI methods usually deal separately with artifacts arising from accelerated data acquisition, involuntary physical motion, and magnetic-field inhomogeneities, leading to suboptimal end-to-end performance. This paper presents CoRRECT, a unified deep unfolding (DU) framework for qMRI consisting of a model-based end-to-end neural network, a method for motion-artifact reduction, and a self-supervised learning scheme. The network is trained to produce R2* maps whose k-space data matches the real data by also accounting for motion and field inhomogeneities. When deployed, CoRRECT only uses the k-space data without any pre-computed parameters for motion or inhomogeneity correction. Our results on experimentally collected multi-Gradient-Recalled Echo (mGRE) MRI data show that CoRRECT recovers motion and inhomogeneity artifact-free R2* maps in highly accelerated acquisition settings. This work opens the door to DU methods that can integrate physical measurement models, biophysical signal models, and learned prior models for high-quality qMRI.

Online Deep Equilibrium Learning for Regularization by Denoising

Plug-and-Play Priors (PnP) and Regularization by Denoising (RED) are widely-used frameworks for solving imaging inverse problems by computing fixed-points of operators combining physical measurement models and learned image priors. While traditional PnP/RED formulations have focused on priors specified using image denoisers, there is a growing interest in learning PnP/RED priors that are end-to-end optimal. The recent Deep Equilibrium Models (DEQ) framework has enabled memory-efficient end-to-end learning of PnP/RED priors by implicitly differentiating through the fixed-point equations without storing intermediate activation values. However, the dependence of the computational/memory complexity of the measurement models in PnP/RED on the total number of measurements leaves DEQ impractical for many imaging applications. We propose ODER as a new strategy for improving the efficiency of DEQ through stochastic approximations of the measurement models. We theoretically analyze ODER giving insights into its convergence and ability to approximate the traditional DEQ approach. Our numerical results suggest the potential improvements in training/testing complexity due to ODER on three distinct imaging applications.

Monotonically Convergent Regularization by Denoising

Regularization by denoising (RED) is a widely-used framework for solving inverse problems by leveraging image denoisers as image priors. Recent work has reported the state-of-the-art performance of RED in a number of imaging applications using pre-trained deep neural nets as denoisers. Despite the recent progress, the stable convergence of RED algorithms remains an open problem. The existing RED theory only guarantees stability for convex data-fidelity terms and nonexpansive denoisers. This work addresses this issue by developing a new monotone RED (MRED) algorithm, whose convergence does not require nonexpansiveness of the deep denoising prior. Simulations on image deblurring and compressive sensing recovery from random matrices show the stability of MRED even when the traditional RED algorithm diverges.

Bregman Plug-and-Play Priors

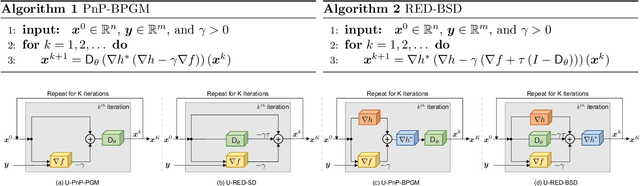
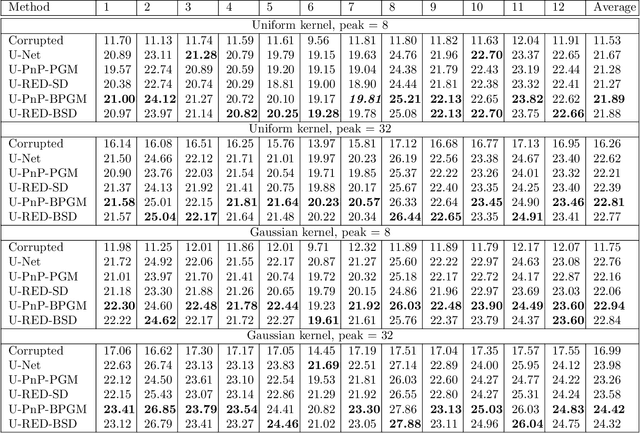
The past few years have seen a surge of activity around integration of deep learning networks and optimization algorithms for solving inverse problems. Recent work on plug-and-play priors (PnP), regularization by denoising (RED), and deep unfolding has shown the state-of-the-art performance of such integration in a variety of applications. However, the current paradigm for designing such algorithms is inherently Euclidean, due to the usage of the quadratic norm within the projection and proximal operators. We propose to broaden this perspective by considering a non-Euclidean setting based on the more general Bregman distance. Our new Bregman Proximal Gradient Method variant of PnP (PnP-BPGM) and Bregman Steepest Descent variant of RED (RED-BSD) replace the traditional updates in PnP and RED from the quadratic norms to more general Bregman distance. We present a theoretical convergence result for PnP-BPGM and demonstrate the effectiveness of our algorithms on Poisson linear inverse problems.

Learning-based Motion Artifact Removal Networks (LEARN) for Quantitative $R_2^\ast$ Mapping

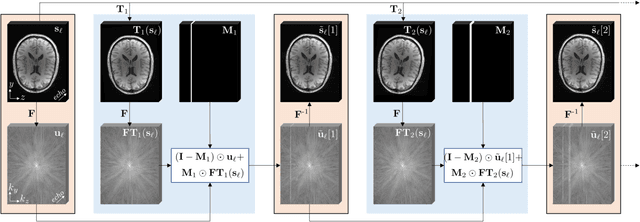
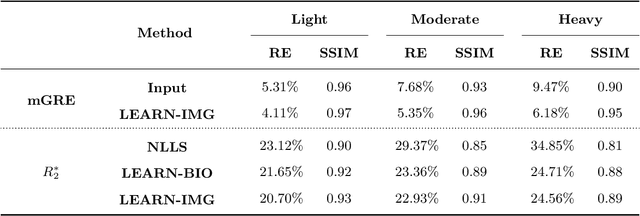
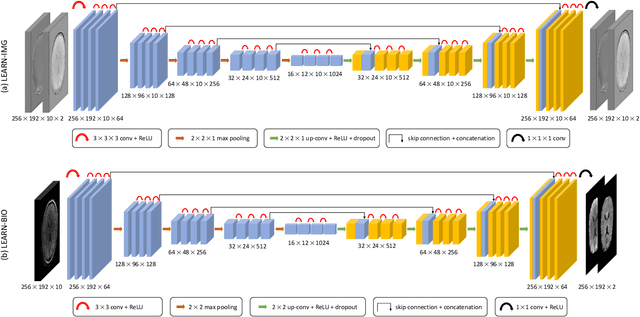
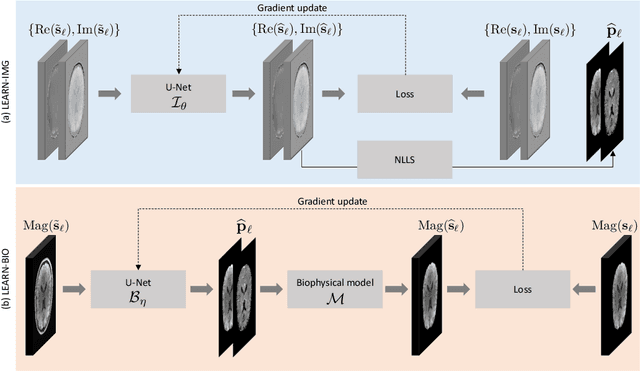
Purpose: To introduce two novel learning-based motion artifact removal networks (LEARN) for the estimation of quantitative motion- and $B0$-inhomogeneity-corrected $R_2^\ast$ maps from motion-corrupted multi-Gradient-Recalled Echo (mGRE) MRI data. Methods: We train two convolutional neural networks (CNNs) to correct motion artifacts for high-quality estimation of quantitative $B0$-inhomogeneity-corrected $R_2^\ast$ maps from mGRE sequences. The first CNN, LEARN-IMG, performs motion correction on complex mGRE images, to enable the subsequent computation of high-quality motion-free quantitative $R_2^\ast$ (and any other mGRE-enabled) maps using the standard voxel-wise analysis or machine-learning-based analysis. The second CNN, LEARN-BIO, is trained to directly generate motion- and $B0$-inhomogeneity-corrected quantitative $R_2^\ast$ maps from motion-corrupted magnitude-only mGRE images by taking advantage of the biophysical model describing the mGRE signal decay. We show that both CNNs trained on synthetic MR images are capable of suppressing motion artifacts while preserving details in the predicted quantitative $R_2^\ast$ maps. Significant reduction of motion artifacts on experimental in vivo motion-corrupted data has also been achieved by using our trained models. Conclusion: Both LEARN-IMG and LEARN-BIO can enable the computation of high-quality motion- and $B0$-inhomogeneity-corrected $R_2^\ast$ maps. LEARN-IMG performs motion correction on mGRE images and relies on the subsequent analysis for the estimation of $R_2^\ast$ maps, while LEARN-BIO directly performs motion- and $B0$-inhomogeneity-corrected $R_2^\ast$ estimation. Both LEARN-IMG and LEARN-BIO jointly process all the available gradient echoes, which enables them to exploit spatial patterns available in the data. The high computational speed of LEARN-BIO is an advantage that can lead to a broader clinical application.