Balasubramanya T. Nadiga
Using Echo-State Networks to Reproduce Rare Events in Chaotic Systems
May 22, 2025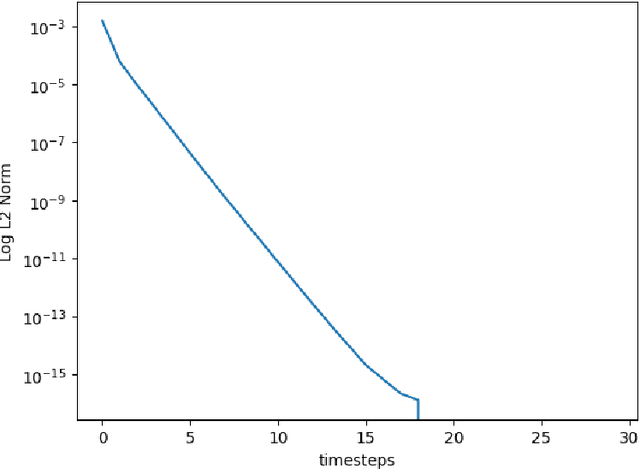
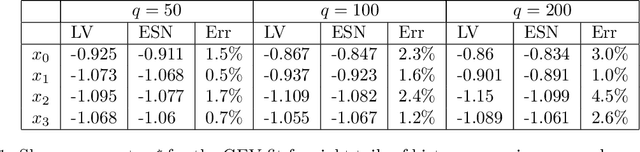
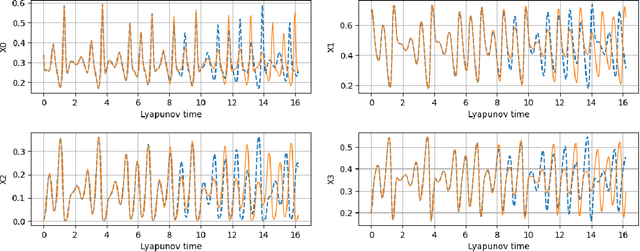
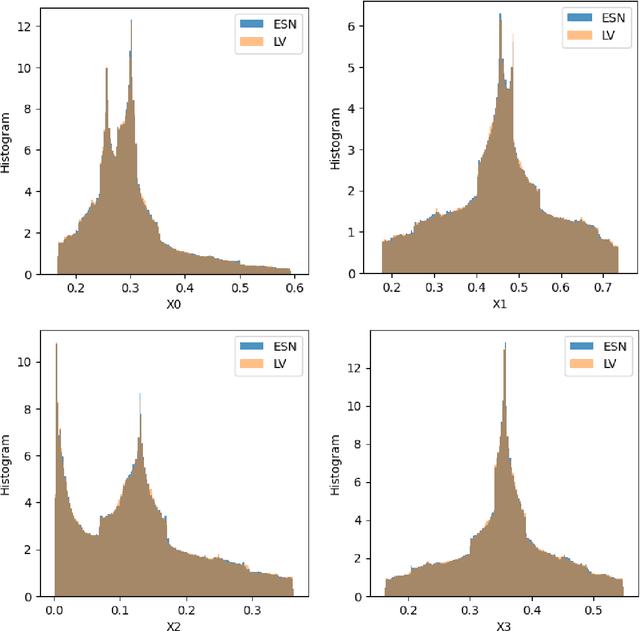
Abstract:We apply the Echo-State Networks to predict the time series and statistical properties of the competitive Lotka-Volterra model in the chaotic regime. In particular, we demonstrate that Echo-State Networks successfully learn the chaotic attractor of the competitive Lotka-Volterra model and reproduce histograms of dependent variables, including tails and rare events. We use the Generalized Extreme Value distribution to quantify the tail behavior.
Learning Robust Features for Scatter Removal and Reconstruction in Dynamic ICF X-Ray Tomography
Aug 22, 2024Abstract:Density reconstruction from X-ray projections is an important problem in radiography with key applications in scientific and industrial X-ray computed tomography (CT). Often, such projections are corrupted by unknown sources of noise and scatter, which when not properly accounted for, can lead to significant errors in density reconstruction. In the setting of this problem, recent deep learning-based methods have shown promise in improving the accuracy of density reconstruction. In this article, we propose a deep learning-based encoder-decoder framework wherein the encoder extracts robust features from noisy/corrupted X-ray projections and the decoder reconstructs the density field from the features extracted by the encoder. We explore three options for the latent-space representation of features: physics-inspired supervision, self-supervision, and no supervision. We find that variants based on self-supervised and physicsinspired supervised features perform better over a range of unknown scatter and noise. In extreme noise settings, the variant with self-supervised features performs best. After investigating further details of the proposed deep-learning methods, we conclude by demonstrating that the newly proposed methods are able to achieve higher accuracy in density reconstruction when compared to a traditional iterative technique.
Reconstructing Richtmyer-Meshkov instabilities from noisy radiographs using low dimensional features and attention-based neural networks
Aug 02, 2024Abstract:A trained attention-based transformer network can robustly recover the complex topologies given by the Richtmyer-Meshkoff instability from a sequence of hydrodynamic features derived from radiographic images corrupted with blur, scatter, and noise. This approach is demonstrated on ICF-like double shell hydrodynamic simulations. The key component of this network is a transformer encoder that acts on a sequence of features extracted from noisy radiographs. This encoder includes numerous self-attention layers that act to learn temporal dependencies in the input sequences and increase the expressiveness of the model. This approach is demonstrated to exhibit an excellent ability to accurately recover the Richtmyer-Meshkov instability growth rates, even despite the gas-metal interface being greatly obscured by radiographic noise.
A Bayesian Deep Learning Approach to Near-Term Climate Prediction
Feb 23, 2022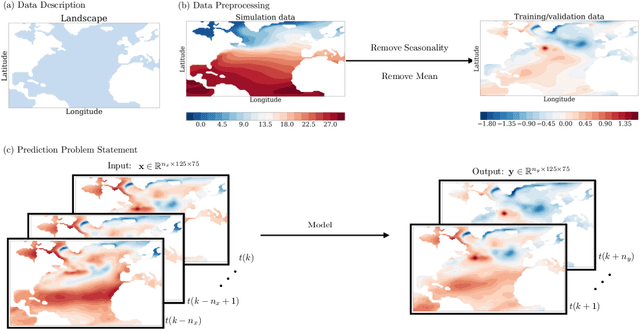
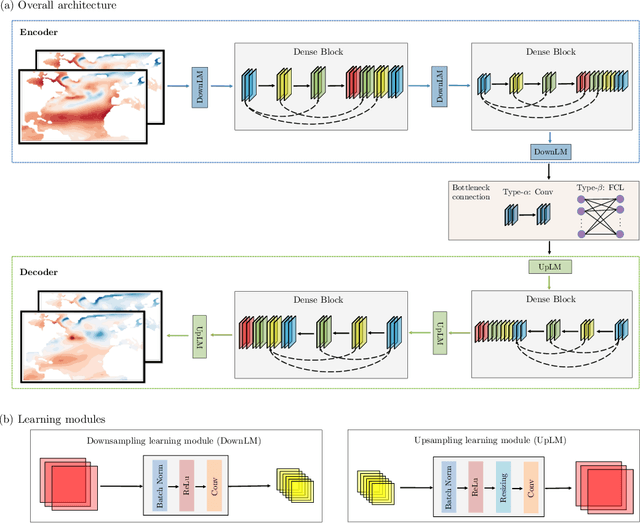
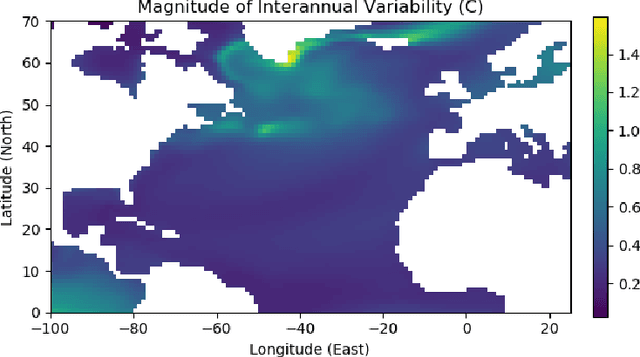
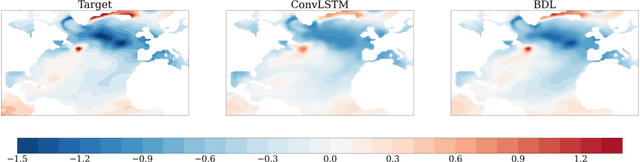
Abstract:Since model bias and associated initialization shock are serious shortcomings that reduce prediction skills in state-of-the-art decadal climate prediction efforts, we pursue a complementary machine-learning-based approach to climate prediction. The example problem setting we consider consists of predicting natural variability of the North Atlantic sea surface temperature on the interannual timescale in the pre-industrial control simulation of the Community Earth System Model (CESM2). While previous works have considered the use of recurrent networks such as convolutional LSTMs and reservoir computing networks in this and other similar problem settings, we currently focus on the use of feedforward convolutional networks. In particular, we find that a feedforward convolutional network with a Densenet architecture is able to outperform a convolutional LSTM in terms of predictive skill. Next, we go on to consider a probabilistic formulation of the same network based on Stein variational gradient descent and find that in addition to providing useful measures of predictive uncertainty, the probabilistic (Bayesian) version improves on its deterministic counterpart in terms of predictive skill. Finally, we characterize the reliability of the ensemble of ML models obtained in the probabilistic setting by using analysis tools developed in the context of ensemble numerical weather prediction.
Predicting Shallow Water Dynamics using Echo-State Networks with Transfer Learning
Dec 16, 2021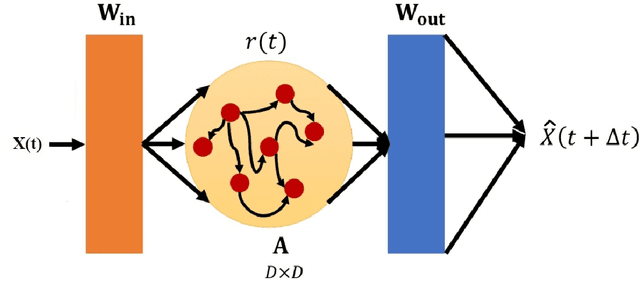
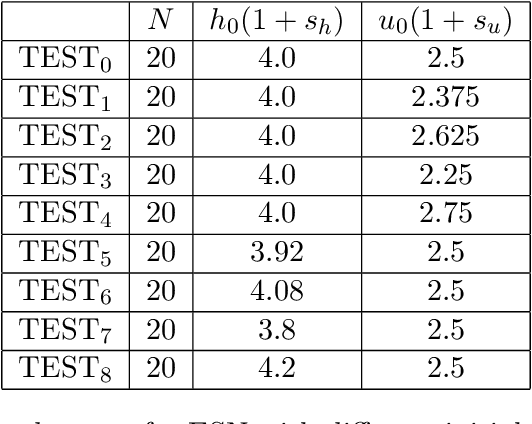
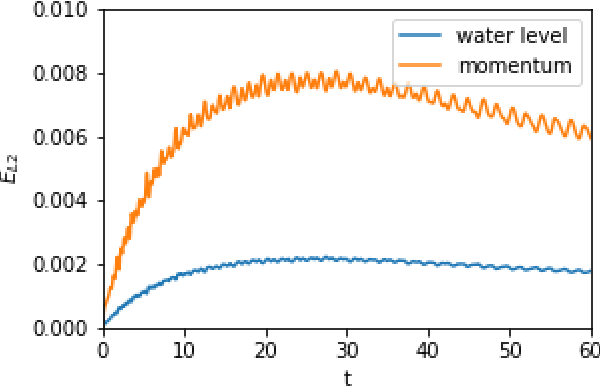
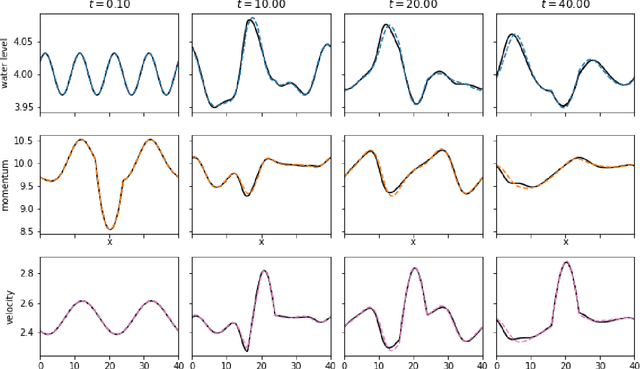
Abstract:In this paper we demonstrate that reservoir computing can be used to learn the dynamics of the shallow-water equations. In particular, while most previous applications of reservoir computing have required training on a particular trajectory to further predict the evolution along that trajectory alone, we show the capability of reservoir computing to predict trajectories of the shallow-water equations with initial conditions not seen in the training process. However, in this setting, we find that the performance of the network deteriorates for initial conditions with ambient conditions (such as total water height and average velocity) that are different from those in the training dataset. To circumvent this deficiency, we introduce a transfer learning approach wherein a small additional training step with the relevant ambient conditions is used to improve the predictions.
High-Precision Inversion of Dynamic Radiography Using Hydrodynamic Features
Dec 02, 2021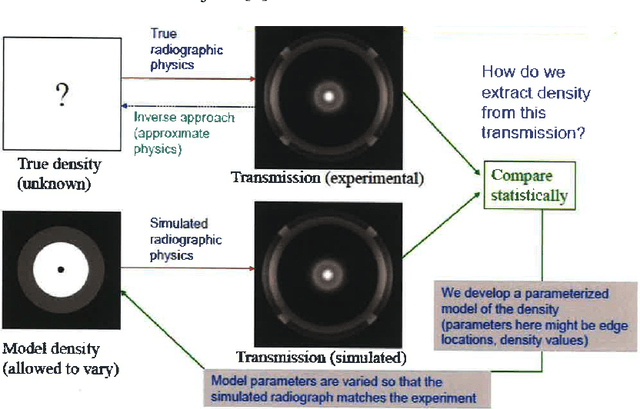

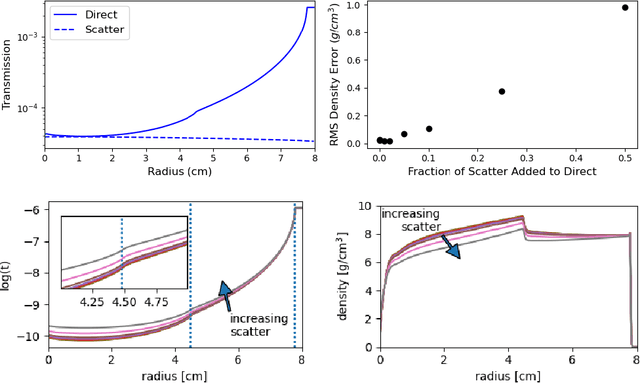
Abstract:Radiography is often used to probe complex, evolving density fields in dynamic systems and in so doing gain insight into the underlying physics. This technique has been used in numerous fields including materials science, shock physics, inertial confinement fusion, and other national security applications. In many of these applications, however, complications resulting from noise, scatter, complex beam dynamics, etc. prevent the reconstruction of density from being accurate enough to identify the underlying physics with sufficient confidence. As such, density reconstruction from static/dynamic radiography has typically been limited to identifying discontinuous features such as cracks and voids in a number of these applications. In this work, we propose a fundamentally new approach to reconstructing density from a temporal sequence of radiographic images. Using only the robust features identifiable in radiographs, we combine them with the underlying hydrodynamic equations of motion using a machine learning approach, namely, conditional generative adversarial networks (cGAN), to determine the density fields from a dynamic sequence of radiographs. Next, we seek to further enhance the hydrodynamic consistency of the ML-based density reconstruction through a process of parameter estimation and projection onto a hydrodynamic manifold. In this context, we note that the distance from the hydrodynamic manifold given by the training data to the test data in the parameter space considered both serves as a diagnostic of the robustness of the predictions and serves to augment the training database, with the expectation that the latter will further reduce future density reconstruction errors. Finally, we demonstrate the ability of this method to outperform a traditional radiographic reconstruction in capturing allowable hydrodynamic paths even when relatively small amounts of scatter are present.
Feature Importance in a Deep Learning Climate Emulator
Aug 27, 2021
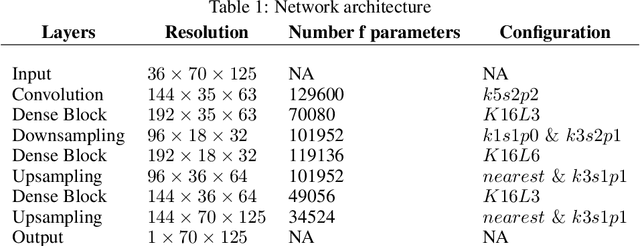
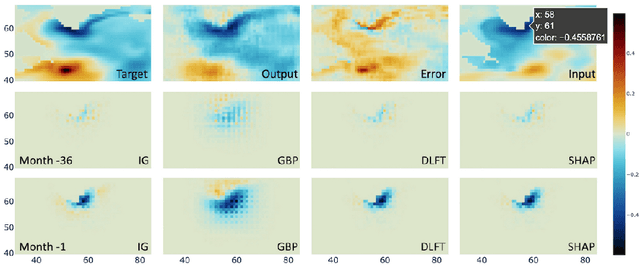
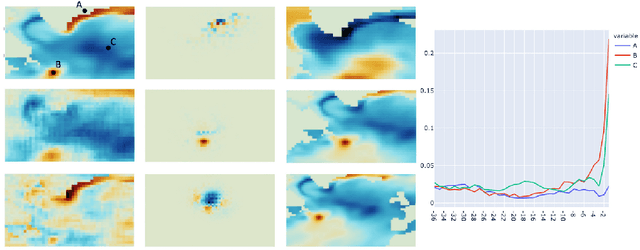
Abstract:We present a study using a class of post-hoc local explanation methods i.e., feature importance methods for "understanding" a deep learning (DL) emulator of climate. Specifically, we consider a multiple-input-single-output emulator that uses a DenseNet encoder-decoder architecture and is trained to predict interannual variations of sea surface temperature (SST) at 1, 6, and 9 month lead times using the preceding 36 months of (appropriately filtered) SST data. First, feature importance methods are employed for individual predictions to spatio-temporally identify input features that are important for model prediction at chosen geographical regions and chosen prediction lead times. In a second step, we also examine the behavior of feature importance in a generalized sense by considering an aggregation of the importance heatmaps over training samples. We find that: 1) the climate emulator's prediction at any geographical location depends dominantly on a small neighborhood around it; 2) the longer the prediction lead time, the further back the "importance" extends; and 3) to leading order, the temporal decay of "importance" is independent of geographical location. An ablation experiment is adopted to verify the findings. From the perspective of climate dynamics, these findings suggest a dominant role for local processes and a negligible role for remote teleconnections at the spatial and temporal scales we consider. From the perspective of network architecture, the spatio-temporal relations between the inputs and outputs we find suggest potential model refinements. We discuss further extensions of our methods, some of which we are considering in ongoing work.
Leveraging Bayesian Analysis To Improve Accuracy of Approximate Models
May 20, 2019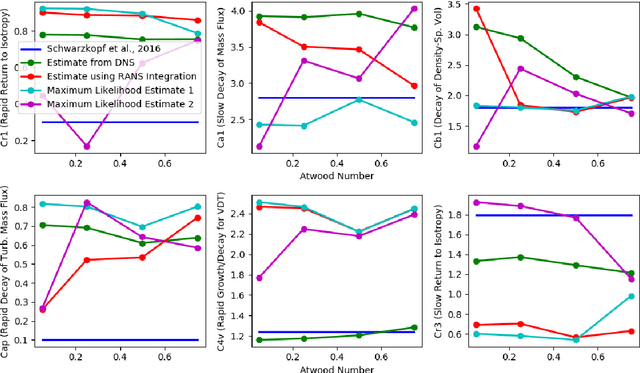
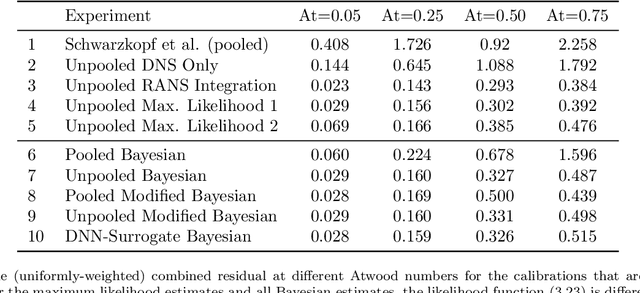
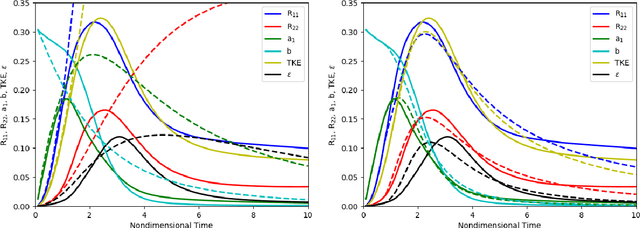

Abstract:We focus on improving the accuracy of an approximate model of a multiscale dynamical system that uses a set of parameter-dependent terms to account for the effects of unresolved or neglected dynamics on resolved scales. We start by considering various methods of calibrating and analyzing such a model given a few well-resolved simulations. After presenting results for various point estimates and discussing some of their shortcomings, we demonstrate (a) the potential of hierarchical Bayesian analysis to uncover previously unanticipated physical dependencies in the approximate model, and (b) how such insights can then be used to improve the model. In effect parametric dependencies found from the Bayesian analysis are used to improve structural aspects of the model. While we choose to illustrate the procedure in the context of a closure model for buoyancy-driven, variable-density turbulence, the statistical nature of the approach makes it more generally applicable. Towards addressing issues of increased computational cost associated with the procedure, we demonstrate the use of a neural network based surrogate in accelerating the posterior sampling process and point to recent developments in variational inference as an alternative methodology for greatly mitigating such costs. We conclude by suggesting that modern validation and uncertainty quantification techniques such as the ones we consider have a valuable role to play in the development and improvement of approximate models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge