Physics-constrained coupled neural differential equations for one dimensional blood flow modeling

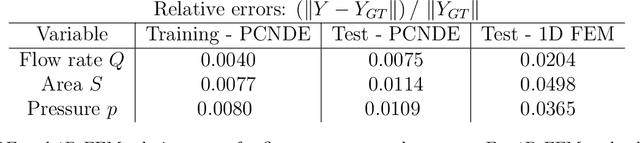
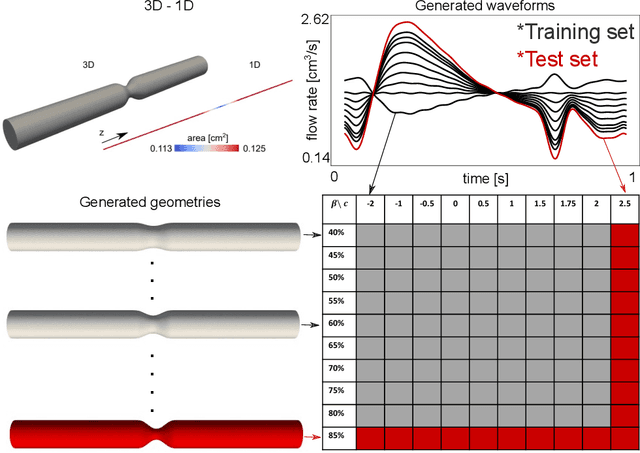
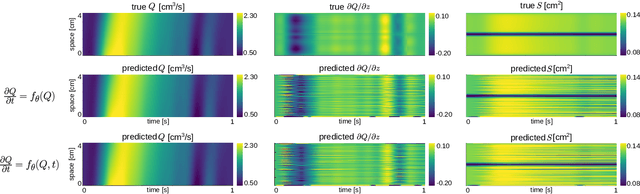
Computational cardiovascular flow modeling plays a crucial role in understanding blood flow dynamics. While 3D models provide acute details, they are computationally expensive, especially with fluid-structure interaction (FSI) simulations. 1D models offer a computationally efficient alternative, by simplifying the 3D Navier-Stokes equations through axisymmetric flow assumption and cross-sectional averaging. However, traditional 1D models based on finite element methods (FEM) often lack accuracy compared to 3D averaged solutions. This study introduces a novel physics-constrained machine learning technique that enhances the accuracy of 1D blood flow models while maintaining computational efficiency. Our approach, utilizing a physics-constrained coupled neural differential equation (PCNDE) framework, demonstrates superior performance compared to conventional FEM-based 1D models across a wide range of inlet boundary condition waveforms and stenosis blockage ratios. A key innovation lies in the spatial formulation of the momentum conservation equation, departing from the traditional temporal approach and capitalizing on the inherent temporal periodicity of blood flow. This spatial neural differential equation formulation switches space and time and overcomes issues related to coupling stability and smoothness, while simplifying boundary condition implementation. The model accurately captures flow rate, area, and pressure variations for unseen waveforms and geometries. We evaluate the model's robustness to input noise and explore the loss landscapes associated with the inclusion of different physics terms. This advanced 1D modeling technique offers promising potential for rapid cardiovascular simulations, achieving computational efficiency and accuracy. By combining the strengths of physics-based and data-driven modeling, this approach enables fast and accurate cardiovascular simulations.

Probabilistic Flux Limiters

The stable numerical integration of shocks in compressible flow simulations relies on the reduction or elimination of Gibbs phenomena (unstable, spurious oscillations). A popular method to virtually eliminate Gibbs oscillations caused by numerical discretization in under-resolved simulations is to use a flux limiter. A wide range of flux limiters has been studied in the literature, with recent interest in their optimization via machine learning methods trained on high-resolution datasets. The common use of flux limiters in numerical codes as plug-and-play blackbox components makes them key targets for design improvement. Moreover, while aleatoric (inherent randomness) and epistemic (lack of knowledge) uncertainty is commonplace in fluid dynamical systems, these effects are generally ignored in the design of flux limiters. Even for deterministic dynamical models, numerical uncertainty is introduced via coarse-graining required by insufficient computational power to solve all scales of motion. Here, we introduce a conceptually distinct type of flux limiter that is designed to handle the effects of randomness in the model and uncertainty in model parameters. This new, {\it probabilistic flux limiter}, learned with high-resolution data, consists of a set of flux limiting functions with associated probabilities, which define the frequencies of selection for their use. Using the example of Burgers' equation, we show that a machine learned, probabilistic flux limiter may be used in a shock capturing code to more accurately capture shock profiles. In particular, we show that our probabilistic flux limiter outperforms standard limiters, and can be successively improved upon (up to a point) by expanding the set of probabilistically chosen flux limiting functions.

Physics-Constrained Generative Adversarial Networks for 3D Turbulence

Generative Adversarial Networks (GANs) have received wide acclaim among the machine learning (ML) community for their ability to generate realistic 2D images. ML is being applied more often to complex problems beyond those of computer vision. However, current frameworks often serve as black boxes and lack physics embeddings, leading to poor ability in enforcing constraints and unreliable models. In this work, we develop physics embeddings that can be stringently imposed, referred to as hard constraints, in the neural network architecture. We demonstrate their capability for 3D turbulence by embedding them in GANs, particularly to enforce the mass conservation constraint in incompressible fluid turbulence. In doing so, we also explore and contrast the effects of other methods of imposing physics constraints within the GANs framework, especially penalty-based physics constraints popular in literature. By using physics-informed diagnostics and statistics, we evaluate the strengths and weaknesses of our approach and demonstrate its feasibility.

Predictive Scale-Bridging Simulations through Active Learning

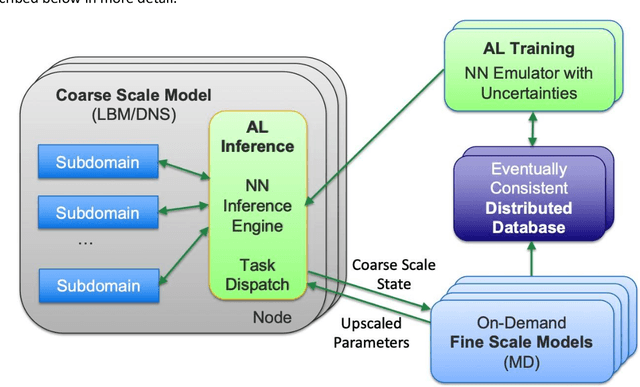
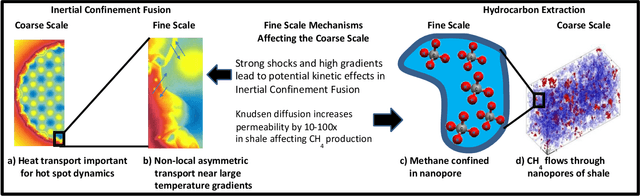
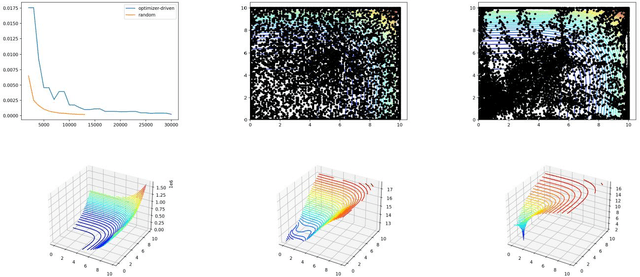
Throughout computational science, there is a growing need to utilize the continual improvements in raw computational horsepower to achieve greater physical fidelity through scale-bridging over brute-force increases in the number of mesh elements. For instance, quantitative predictions of transport in nanoporous media, critical to hydrocarbon extraction from tight shale formations, are impossible without accounting for molecular-level interactions. Similarly, inertial confinement fusion simulations rely on numerical diffusion to simulate molecular effects such as non-local transport and mixing without truly accounting for molecular interactions. With these two disparate applications in mind, we develop a novel capability which uses an active learning approach to optimize the use of local fine-scale simulations for informing coarse-scale hydrodynamics. Our approach addresses three challenges: forecasting continuum coarse-scale trajectory to speculatively execute new fine-scale molecular dynamics calculations, dynamically updating coarse-scale from fine-scale calculations, and quantifying uncertainty in neural network models.

Regression-based projection for learning Mori--Zwanzig operators

We propose to adopt statistical regression as the projection operator to enable data-driven learning of the operators in the Mori--Zwanzig formalism. We present a principled algorithm to extract the Markov and memory operators for any regression models. We show that the choice of linear regression results in a recently proposed data-driven learning algorithm based on Mori's projection operator, which can be considered as a higher-order approximate Koopman learning method. We show that more expressive, potentially nonlinear regression models naturally fill in the gap between the highly idealized and computationally efficient Mori's projection operator and the most optimal yet computationally infeasible Zwanzig projection operator. We performed numerical experiments and extracted the operators for an array of regression-based projections, including linear, polynomial, spline, and neural-network-based regression, showing a progressive improvement as the complexity of the regression model increased. Our proposition provides a general framework to extract memory-dependent corrections and can be readily applied to an array of data-driven learning methods for stationary dynamical systems in the literature.

Physics Informed Machine Learning of SPH: Machine Learning Lagrangian Turbulence

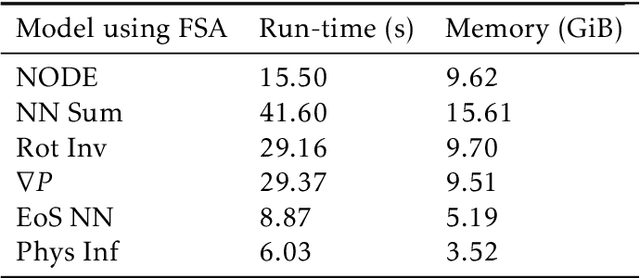
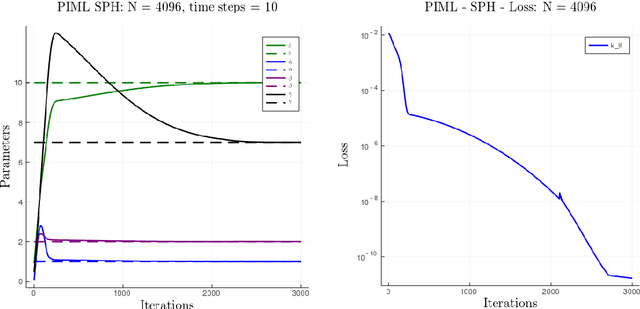
Smoothed particle hydrodynamics (SPH) is a mesh-free Lagrangian method for obtaining approximate numerical solutions of the equations of fluid dynamics; which has been widely applied to weakly- and strongly compressible turbulence in astrophysics and engineering applications. We present a learn-able hierarchy of parameterized and "physics-explainable" SPH informed fluid simulators using both physics based parameters and Neural Networks (NNs) as universal function approximators. Our learning algorithm develops a mixed mode approach, mixing forward and reverse mode automatic differentiation with forward and adjoint based sensitivity analyses to efficiently perform gradient based optimization. We show that our physics informed learning method is capable of: (a) solving inverse problems over the physically interpretable parameter space, as well as over the space of NN parameters; (b) learning Lagrangian statistics of turbulence (interpolation); (c) combining Lagrangian trajectory based, probabilistic, and Eulerian field based loss functions; and (d) extrapolating beyond training sets into more complex regimes of interest. Furthermore, this hierarchy of models gradually introduces more physical structure, which we show improves interpretability, generalizability (over larger ranges of time scales and Reynolds numbers), preservation of physical symmetries, and requires less training data.

Objective discovery of dominant dynamical processes with intelligible machine learning

The advent of big data has vast potential for discovery in natural phenomena ranging from climate science to medicine, but overwhelming complexity stymies insight. Existing theory is often not able to succinctly describe salient phenomena, and progress has largely relied on ad hoc definitions of dynamical regimes to guide and focus exploration. We present a formal definition in which the identification of dynamical regimes is formulated as an optimization problem, and we propose an intelligible objective function. Furthermore, we propose an unsupervised learning framework which eliminates the need for a priori knowledge and ad hoc definitions; instead, the user need only choose appropriate clustering and dimensionality reduction algorithms, and this choice can be guided using our proposed objective function. We illustrate its applicability with example problems drawn from ocean dynamics, tumor angiogenesis, and turbulent boundary layers. Our method is a step towards unbiased data exploration that allows serendipitous discovery within dynamical systems, with the potential to propel the physical sciences forward.

Leveraging Bayesian Analysis To Improve Accuracy of Approximate Models

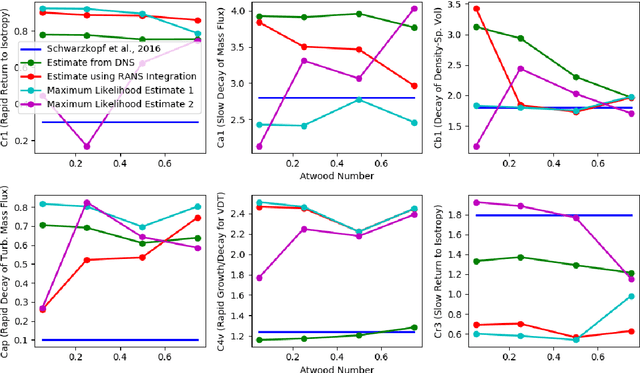
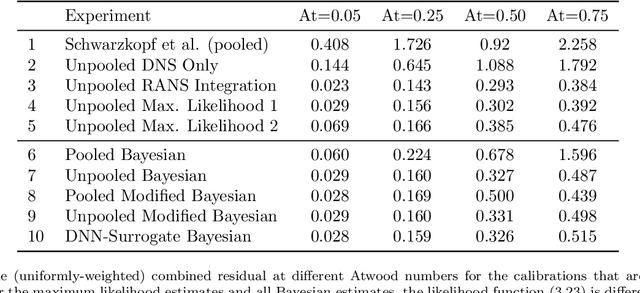
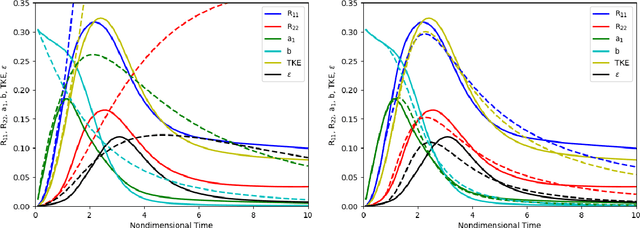
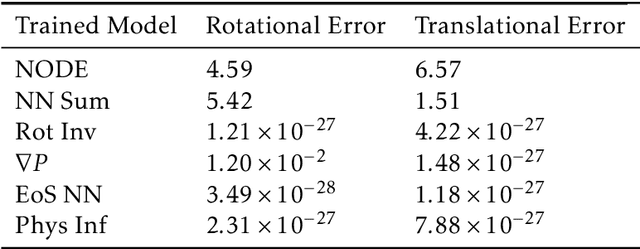
We focus on improving the accuracy of an approximate model of a multiscale dynamical system that uses a set of parameter-dependent terms to account for the effects of unresolved or neglected dynamics on resolved scales. We start by considering various methods of calibrating and analyzing such a model given a few well-resolved simulations. After presenting results for various point estimates and discussing some of their shortcomings, we demonstrate (a) the potential of hierarchical Bayesian analysis to uncover previously unanticipated physical dependencies in the approximate model, and (b) how such insights can then be used to improve the model. In effect parametric dependencies found from the Bayesian analysis are used to improve structural aspects of the model. While we choose to illustrate the procedure in the context of a closure model for buoyancy-driven, variable-density turbulence, the statistical nature of the approach makes it more generally applicable. Towards addressing issues of increased computational cost associated with the procedure, we demonstrate the use of a neural network based surrogate in accelerating the posterior sampling process and point to recent developments in variational inference as an alternative methodology for greatly mitigating such costs. We conclude by suggesting that modern validation and uncertainty quantification techniques such as the ones we consider have a valuable role to play in the development and improvement of approximate models.