Physics-constrained coupled neural differential equations for one dimensional blood flow modeling
Paper and Code
Nov 08, 2024
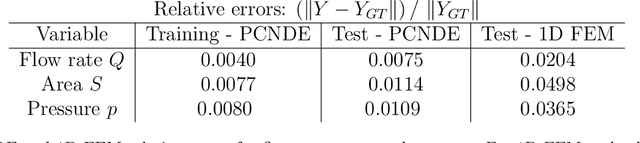
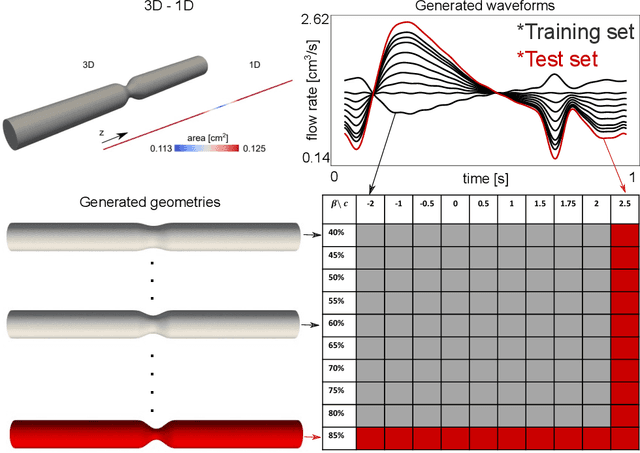
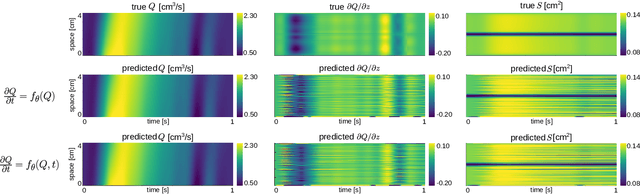
Computational cardiovascular flow modeling plays a crucial role in understanding blood flow dynamics. While 3D models provide acute details, they are computationally expensive, especially with fluid-structure interaction (FSI) simulations. 1D models offer a computationally efficient alternative, by simplifying the 3D Navier-Stokes equations through axisymmetric flow assumption and cross-sectional averaging. However, traditional 1D models based on finite element methods (FEM) often lack accuracy compared to 3D averaged solutions. This study introduces a novel physics-constrained machine learning technique that enhances the accuracy of 1D blood flow models while maintaining computational efficiency. Our approach, utilizing a physics-constrained coupled neural differential equation (PCNDE) framework, demonstrates superior performance compared to conventional FEM-based 1D models across a wide range of inlet boundary condition waveforms and stenosis blockage ratios. A key innovation lies in the spatial formulation of the momentum conservation equation, departing from the traditional temporal approach and capitalizing on the inherent temporal periodicity of blood flow. This spatial neural differential equation formulation switches space and time and overcomes issues related to coupling stability and smoothness, while simplifying boundary condition implementation. The model accurately captures flow rate, area, and pressure variations for unseen waveforms and geometries. We evaluate the model's robustness to input noise and explore the loss landscapes associated with the inclusion of different physics terms. This advanced 1D modeling technique offers promising potential for rapid cardiovascular simulations, achieving computational efficiency and accuracy. By combining the strengths of physics-based and data-driven modeling, this approach enables fast and accurate cardiovascular simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge