What You See is Not What You Get: Neural Partial Differential Equations and The Illusion of Learning

Differentiable Programming for scientific machine learning (SciML) has recently seen considerable interest and success, as it directly embeds neural networks inside PDEs, often called as NeuralPDEs, derived from first principle physics. Therefore, there is a widespread assumption in the community that NeuralPDEs are more trustworthy and generalizable than black box models. However, like any SciML model, differentiable programming relies predominantly on high-quality PDE simulations as "ground truth" for training. However, mathematics dictates that these are only discrete numerical approximations of the true physics. Therefore, we ask: Are NeuralPDEs and differentiable programming models trained on PDE simulations as physically interpretable as we think? In this work, we rigorously attempt to answer these questions, using established ideas from numerical analysis, experiments, and analysis of model Jacobians. Our study shows that NeuralPDEs learn the artifacts in the simulation training data arising from the discretized Taylor Series truncation error of the spatial derivatives. Additionally, NeuralPDE models are systematically biased, and their generalization capability is likely enabled by a fortuitous interplay of numerical dissipation and truncation error in the training dataset and NeuralPDE, which seldom happens in practical applications. This bias manifests aggressively even in relatively accessible 1-D equations, raising concerns about the veracity of differentiable programming on complex, high-dimensional, real-world PDEs, and in dataset integrity of foundation models. Further, we observe that the initial condition constrains the truncation error in initial-value problems in PDEs, thereby exerting limitations to extrapolation. Finally, we demonstrate that an eigenanalysis of model weights can indicate a priori if the model will be inaccurate for out-of-distribution testing.

Machine learned reconstruction of tsunami dynamics from sparse observations

We investigate the use of the Senseiver, a transformer neural network designed for sparse sensing applications, to estimate full-field surface height measurements of tsunami waves from sparse observations. The model is trained on a large ensemble of simulated data generated via a shallow water equations solver, which we show to be a faithful reproduction for the underlying dynamics by comparison to historical events. We train the model on a dataset consisting of 8 tsunami simulations whose epicenters correspond to historical USGS earthquake records, and where the model inputs are restricted to measurements obtained at actively deployed buoy locations. We test the Senseiver on a dataset consisting of 8 simulations not included in training, demonstrating its capability for extrapolation. The results show remarkable resolution of fine scale phase and amplitude features from the true field, provided that at least a few of the sensors have obtained a non-zero signal. Throughout, we discuss which forecasting techniques can be improved by this method, and suggest ways in which the flexibility of the architecture can be leveraged to incorporate arbitrary remote sensing data (eg. HF Radar and satellite measurements) as well as investigate optimal sensor placements.

Physics-constrained coupled neural differential equations for one dimensional blood flow modeling

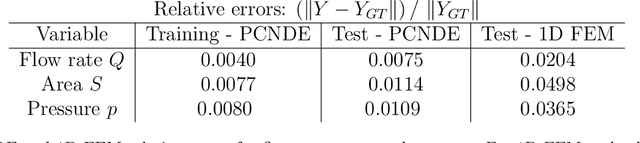
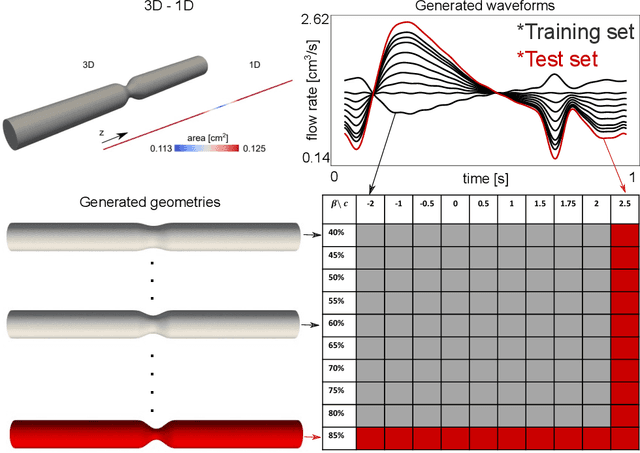
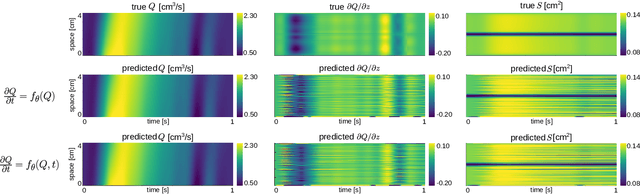
Computational cardiovascular flow modeling plays a crucial role in understanding blood flow dynamics. While 3D models provide acute details, they are computationally expensive, especially with fluid-structure interaction (FSI) simulations. 1D models offer a computationally efficient alternative, by simplifying the 3D Navier-Stokes equations through axisymmetric flow assumption and cross-sectional averaging. However, traditional 1D models based on finite element methods (FEM) often lack accuracy compared to 3D averaged solutions. This study introduces a novel physics-constrained machine learning technique that enhances the accuracy of 1D blood flow models while maintaining computational efficiency. Our approach, utilizing a physics-constrained coupled neural differential equation (PCNDE) framework, demonstrates superior performance compared to conventional FEM-based 1D models across a wide range of inlet boundary condition waveforms and stenosis blockage ratios. A key innovation lies in the spatial formulation of the momentum conservation equation, departing from the traditional temporal approach and capitalizing on the inherent temporal periodicity of blood flow. This spatial neural differential equation formulation switches space and time and overcomes issues related to coupling stability and smoothness, while simplifying boundary condition implementation. The model accurately captures flow rate, area, and pressure variations for unseen waveforms and geometries. We evaluate the model's robustness to input noise and explore the loss landscapes associated with the inclusion of different physics terms. This advanced 1D modeling technique offers promising potential for rapid cardiovascular simulations, achieving computational efficiency and accuracy. By combining the strengths of physics-based and data-driven modeling, this approach enables fast and accurate cardiovascular simulations.

Machine Learning technique for isotopic determination of radioisotopes using HPGe $\mathrmγ$-ray spectra

$\mathrm{\gamma}$-ray spectroscopy is a quantitative, non-destructive technique that may be utilized for the identification and quantitative isotopic estimation of radionuclides. Traditional methods of isotopic determination have various challenges that contribute to statistical and systematic uncertainties in the estimated isotopics. Furthermore, these methods typically require numerous pre-processing steps, and have only been rigorously tested in laboratory settings with limited shielding. In this work, we examine the application of a number of machine learning based regression algorithms as alternatives to conventional approaches for analyzing $\mathrm{\gamma}$-ray spectroscopy data in the Emergency Response arena. This approach not only eliminates many steps in the analysis procedure, and therefore offers potential to reduce this source of systematic uncertainty, but is also shown to offer comparable performance to conventional approaches in the Emergency Response Application.

The ISTI Rapid Response on Exploring Cloud Computing 2018

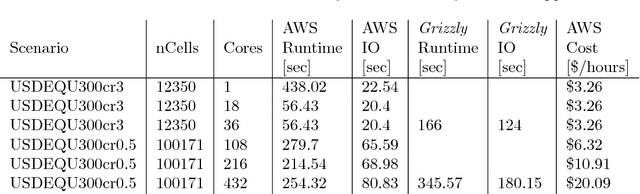
This report describes eighteen projects that explored how commercial cloud computing services can be utilized for scientific computation at national laboratories. These demonstrations ranged from deploying proprietary software in a cloud environment to leveraging established cloud-based analytics workflows for processing scientific datasets. By and large, the projects were successful and collectively they suggest that cloud computing can be a valuable computational resource for scientific computation at national laboratories.

From Deep to Physics-Informed Learning of Turbulence: Diagnostics

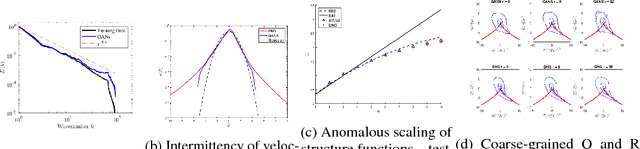
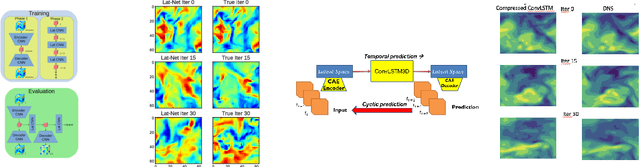
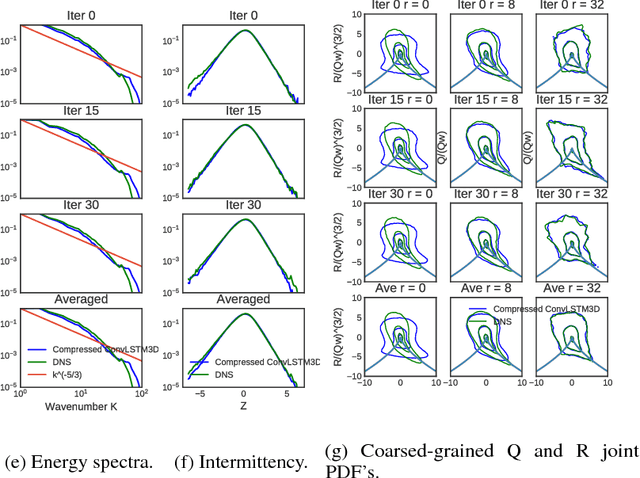
We describe physical tests validating progress made toward acceleration and automation of hydrodynamic codes in the regime of developed turbulence by two {\bf Deep Learning} (DL) Neural Network (NN) schemes trained on {\bf Direct Numerical Simulations} of turbulence. Even the bare DL solutions, which do not take into account any physics of turbulence explicitly, are impressively good overall when it comes to qualitative description of important features of turbulence. However, the early tests have also uncovered some caveats of the DL approaches. We observe that the static DL scheme, implementing Convolutional GAN and trained on spatial snapshots of turbulence, fails to reproduce intermittency of turbulent fluctuations at small scales and details of the turbulence geometry at large scales. We show that the dynamic NN scheme, LAT-NET, trained on a temporal sequence of turbulence snapshots is capable to correct for the small-scale caveat of the static NN. We suggest a path forward towards improving reproducibility of the large-scale geometry of turbulence with NN.