Learning physical unknowns from hydrodynamic shock and material interface features in ICF capsule implosions

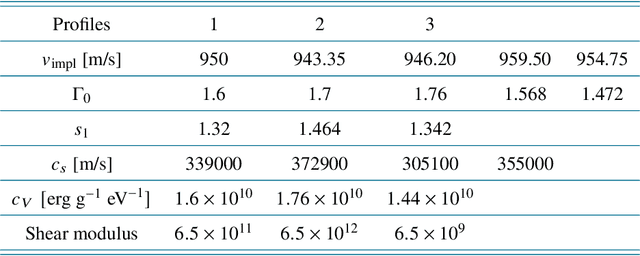
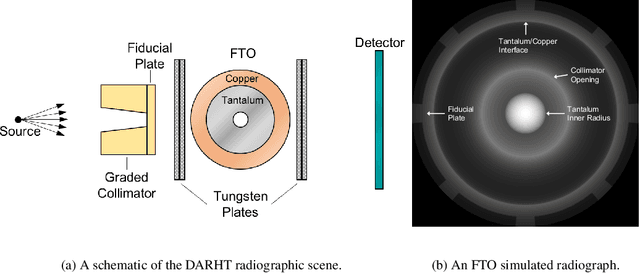
In high energy density physics (HEDP) and inertial confinement fusion (ICF), predictive modeling is complicated by uncertainty in parameters that characterize various aspects of the modeled system, such as those characterizing material properties, equation of state (EOS), opacities, and initial conditions. Typically, however, these parameters are not directly observable. What is observed instead is a time sequence of radiographic projections using X-rays. In this work, we define a set of sparse hydrodynamic features derived from the outgoing shock profile and outer material edge, which can be obtained from radiographic measurements, to directly infer such parameters. Our machine learning (ML)-based methodology involves a pipeline of two architectures, a radiograph-to-features network (R2FNet) and a features-to-parameters network (F2PNet), that are trained independently and later combined to approximate a posterior distribution for the parameters from radiographs. We show that the estimated parameters can be used in a hydrodynamics code to obtain density fields and hydrodynamic shock and outer edge features that are consistent with the data. Finally, we demonstrate that features resulting from an unknown EOS model can be successfully mapped onto parameters of a chosen analytical EOS model, implying that network predictions are learning physics, with a degree of invariance to the underlying choice of EOS model.

Supervised Reconstruction for Silhouette Tomography

In this paper, we introduce silhouette tomography, a novel formulation of X-ray computed tomography that relies only on the geometry of the imaging system. We formulate silhouette tomography mathematically and provide a simple method for obtaining a particular solution to the problem, assuming that any solution exists. We then propose a supervised reconstruction approach that uses a deep neural network to solve the silhouette tomography problem. We present experimental results on a synthetic dataset that demonstrate the effectiveness of the proposed method.

Machine Learning technique for isotopic determination of radioisotopes using HPGe $\mathrmγ$-ray spectra

$\mathrm{\gamma}$-ray spectroscopy is a quantitative, non-destructive technique that may be utilized for the identification and quantitative isotopic estimation of radionuclides. Traditional methods of isotopic determination have various challenges that contribute to statistical and systematic uncertainties in the estimated isotopics. Furthermore, these methods typically require numerous pre-processing steps, and have only been rigorously tested in laboratory settings with limited shielding. In this work, we examine the application of a number of machine learning based regression algorithms as alternatives to conventional approaches for analyzing $\mathrm{\gamma}$-ray spectroscopy data in the Emergency Response arena. This approach not only eliminates many steps in the analysis procedure, and therefore offers potential to reduce this source of systematic uncertainty, but is also shown to offer comparable performance to conventional approaches in the Emergency Response Application.

Sparse-view Cone Beam CT Reconstruction using Data-consistent Supervised and Adversarial Learning from Scarce Training Data

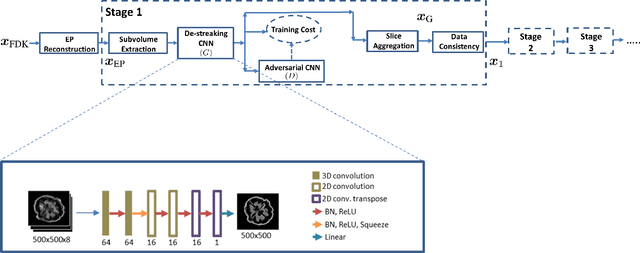
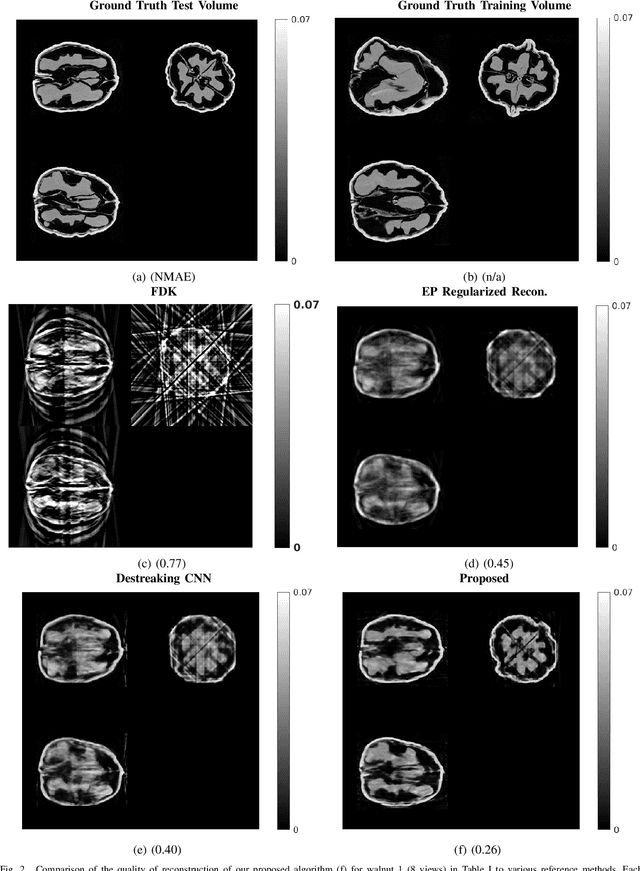
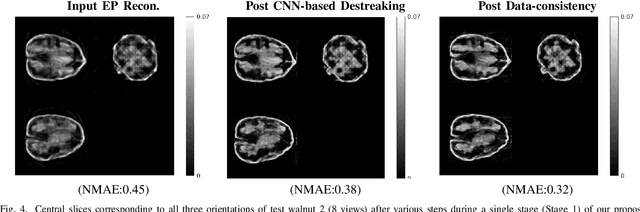
Reconstruction of CT images from a limited set of projections through an object is important in several applications ranging from medical imaging to industrial settings. As the number of available projections decreases, traditional reconstruction techniques such as the FDK algorithm and model-based iterative reconstruction methods perform poorly. Recently, data-driven methods such as deep learning-based reconstruction have garnered a lot of attention in applications because they yield better performance when enough training data is available. However, even these methods have their limitations when there is a scarcity of available training data. This work focuses on image reconstruction in such settings, i.e., when both the number of available CT projections and the training data is extremely limited. We adopt a sequential reconstruction approach over several stages using an adversarially trained shallow network for 'destreaking' followed by a data-consistency update in each stage. To deal with the challenge of limited data, we use image subvolumes to train our method, and patch aggregation during testing. To deal with the computational challenge of learning on 3D datasets for 3D reconstruction, we use a hybrid 3D-to-2D mapping network for the 'destreaking' part. Comparisons to other methods over several test examples indicate that the proposed method has much potential, when both the number of projections and available training data are highly limited.

Physics-Driven Learning of Wasserstein GAN for Density Reconstruction in Dynamic Tomography

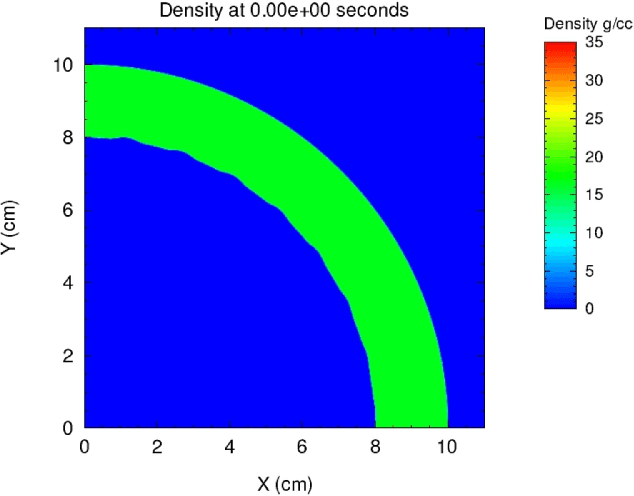
Object density reconstruction from projections containing scattered radiation and noise is of critical importance in many applications. Existing scatter correction and density reconstruction methods may not provide the high accuracy needed in many applications and can break down in the presence of unmodeled or anomalous scatter and other experimental artifacts. Incorporating machine-learned models could prove beneficial for accurate density reconstruction particularly in dynamic imaging, where the time-evolution of the density fields could be captured by partial differential equations or by learning from hydrodynamics simulations. In this work, we demonstrate the ability of learned deep neural networks to perform artifact removal in noisy density reconstructions, where the noise is imperfectly characterized. We use a Wasserstein generative adversarial network (WGAN), where the generator serves as a denoiser that removes artifacts in densities obtained from traditional reconstruction algorithms. We train the networks from large density time-series datasets, with noise simulated according to parametric random distributions that may mimic noise in experiments. The WGAN is trained with noisy density frames as generator inputs, to match the generator outputs to the distribution of clean densities (time-series) from simulations. A supervised loss is also included in the training, which leads to improved density restoration performance. In addition, we employ physics-based constraints such as mass conservation during network training and application to further enable highly accurate density reconstructions. Our preliminary numerical results show that the models trained in our frameworks can remove significant portions of unknown noise in density time-series data.