An Adaptive Multiparameter Penalty Selection Method for Multiconstraint and Multiblock ADMM

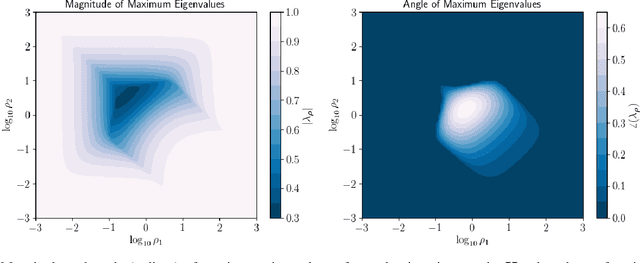
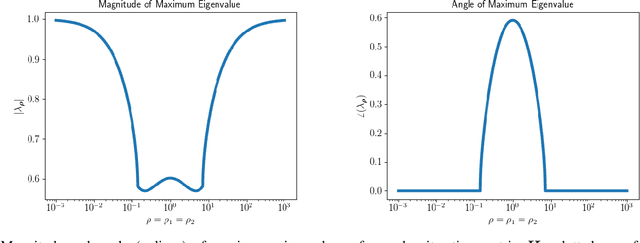
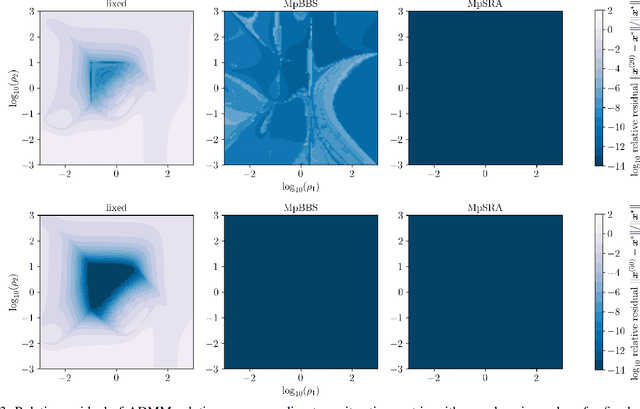
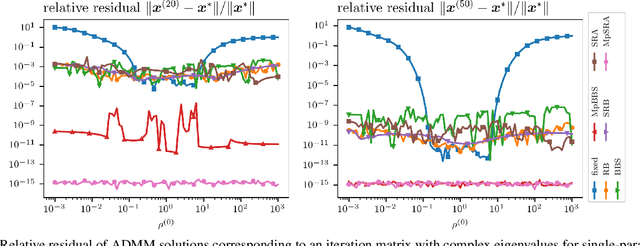
This work presents a new method for online selection of multiple penalty parameters for the alternating direction method of multipliers (ADMM) algorithm applied to optimization problems with multiple constraints or functionals with block matrix components. ADMM is widely used for solving constrained optimization problems in a variety of fields, including signal and image processing. Implementations of ADMM often utilize a single hyperparameter, referred to as the penalty parameter, which needs to be tuned to control the rate of convergence. However, in problems with multiple constraints, ADMM may demonstrate slow convergence regardless of penalty parameter selection due to scale differences between constraints. Accounting for scale differences between constraints to improve convergence in these cases requires introducing a penalty parameter for each constraint. The proposed method is able to adaptively account for differences in scale between constraints, providing robustness with respect to problem transformations and initial selection of penalty parameters. It is also simple to understand and implement. Our numerical experiments demonstrate that the proposed method performs favorably compared to a variety of existing penalty parameter selection methods.

Plug-and-Play Priors as a Score-Based Method

Plug-and-play (PnP) methods are extensively used for solving imaging inverse problems by integrating physical measurement models with pre-trained deep denoisers as priors. Score-based diffusion models (SBMs) have recently emerged as a powerful framework for image generation by training deep denoisers to represent the score of the image prior. While both PnP and SBMs use deep denoisers, the score-based nature of PnP is unexplored in the literature due to its distinct origins rooted in proximal optimization. This letter introduces a novel view of PnP as a score-based method, a perspective that enables the re-use of powerful SBMs within classical PnP algorithms without retraining. We present a set of mathematical relationships for adapting popular SBMs as priors within PnP. We show that this approach enables a direct comparison between PnP and SBM-based reconstruction methods using the same neural network as the prior. Code is available at https://github.com/wustl-cig/score_pnp.

Random Walks with Tweedie: A Unified Framework for Diffusion Models

We present a simple template for designing generative diffusion model algorithms based on an interpretation of diffusion sampling as a sequence of random walks. Score-based diffusion models are widely used to generate high-quality images. Diffusion models have also been shown to yield state-of-the-art performance in many inverse problems. While these algorithms are often surprisingly simple, the theory behind them is not, and multiple complex theoretical justifications exist in the literature. Here, we provide a simple and largely self-contained theoretical justification for score-based-diffusion models that avoids using the theory of Markov chains or reverse diffusion, instead centering the theory of random walks and Tweedie's formula. This approach leads to unified algorithmic templates for network training and sampling. In particular, these templates cleanly separate training from sampling, e.g., the noise schedule used during training need not match the one used during sampling. We show that several existing diffusion models correspond to particular choices within this template and demonstrate that other, more straightforward algorithmic choices lead to effective diffusion models. The proposed framework has the added benefit of enabling conditional sampling without any likelihood approximation.

Supervised Reconstruction for Silhouette Tomography

In this paper, we introduce silhouette tomography, a novel formulation of X-ray computed tomography that relies only on the geometry of the imaging system. We formulate silhouette tomography mathematically and provide a simple method for obtaining a particular solution to the problem, assuming that any solution exists. We then propose a supervised reconstruction approach that uses a deep neural network to solve the silhouette tomography problem. We present experimental results on a synthetic dataset that demonstrate the effectiveness of the proposed method.

Score-based Diffusion Models for Bayesian Image Reconstruction

This paper explores the use of score-based diffusion models for Bayesian image reconstruction. Diffusion models are an efficient tool for generative modeling. Diffusion models can also be used for solving image reconstruction problems. We present a simple and flexible algorithm for training a diffusion model and using it for maximum a posteriori reconstruction, minimum mean square error reconstruction, and posterior sampling. We present experiments on both a linear and a nonlinear reconstruction problem that highlight the strengths and limitations of the approach.

Material Identification From Radiographs Without Energy Resolution

We propose a method for performing material identification from radiographs without energy-resolved measurements. Material identification has a wide variety of applications, including in biomedical imaging, nondestructive testing, and security. While existing techniques for radiographic material identification make use of dual energy sources, energy-resolving detectors, or additional (e.g., neutron) measurements, such setups are not always practical-requiring additional hardware and complicating imaging. We tackle material identification without energy resolution, allowing standard X-ray systems to provide material identification information without requiring additional hardware. Assuming a setting where the geometry of each object in the scene is known and the materials come from a known set of possible materials, we pose the problem as a combinatorial optimization with a loss function that accounts for the presence of scatter and an unknown gain and propose a branch and bound algorithm to efficiently solve it. We present experiments on both synthetic data and real, experimental data with relevance to security applications-thick, dense objects imaged with MeV X-rays. We show that material identification can be efficient and accurate, for example, in a scene with three shells (two copper, one aluminum), our algorithm ran in six minutes on a consumer-level laptop and identified the correct materials as being among the top 10 best matches out of 8,000 possibilities.

Solving 3D Inverse Problems using Pre-trained 2D Diffusion Models

Diffusion models have emerged as the new state-of-the-art generative model with high quality samples, with intriguing properties such as mode coverage and high flexibility. They have also been shown to be effective inverse problem solvers, acting as the prior of the distribution, while the information of the forward model can be granted at the sampling stage. Nonetheless, as the generative process remains in the same high dimensional (i.e. identical to data dimension) space, the models have not been extended to 3D inverse problems due to the extremely high memory and computational cost. In this paper, we combine the ideas from the conventional model-based iterative reconstruction with the modern diffusion models, which leads to a highly effective method for solving 3D medical image reconstruction tasks such as sparse-view tomography, limited angle tomography, compressed sensing MRI from pre-trained 2D diffusion models. In essence, we propose to augment the 2D diffusion prior with a model-based prior in the remaining direction at test time, such that one can achieve coherent reconstructions across all dimensions. Our method can be run in a single commodity GPU, and establishes the new state-of-the-art, showing that the proposed method can perform reconstructions of high fidelity and accuracy even in the most extreme cases (e.g. 2-view 3D tomography). We further reveal that the generalization capacity of the proposed method is surprisingly high, and can be used to reconstruct volumes that are entirely different from the training dataset.

Learning Sparsity-Promoting Regularizers using Bilevel Optimization

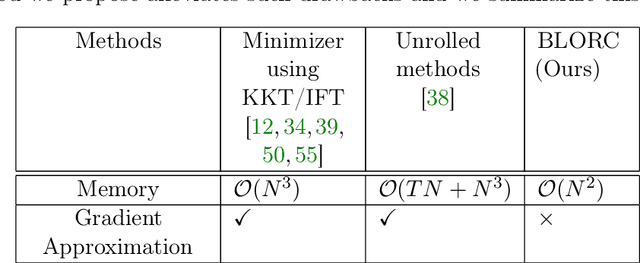
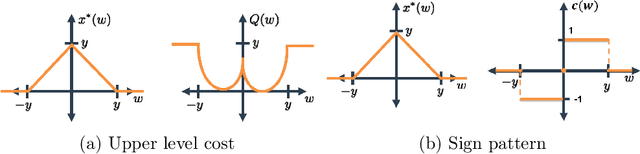
We present a method for supervised learning of sparsity-promoting regularizers for denoising signals and images. Sparsity-promoting regularization is a key ingredient in solving modern signal reconstruction problems; however, the operators underlying these regularizers are usually either designed by hand or learned from data in an unsupervised way. The recent success of supervised learning (mainly convolutional neural networks) in solving image reconstruction problems suggests that it could be a fruitful approach to designing regularizers. Towards this end, we propose to denoise signals using a variational formulation with a parametric, sparsity-promoting regularizer, where the parameters of the regularizer are learned to minimize the mean squared error of reconstructions on a training set of ground truth image and measurement pairs. Training involves solving a challenging bilievel optimization problem; we derive an expression for the gradient of the training loss using the closed-form solution of the denoising problem and provide an accompanying gradient descent algorithm to minimize it. Our experiments with structured 1D signals and natural images show that the proposed method can learn an operator that outperforms well-known regularizers (total variation, DCT-sparsity, and unsupervised dictionary learning) and collaborative filtering for denoising. While the approach we present is specific to denoising, we believe that it could be adapted to the larger class of inverse problems with linear measurement models, giving it applicability in a wide range of signal reconstruction settings.

High-Precision Inversion of Dynamic Radiography Using Hydrodynamic Features

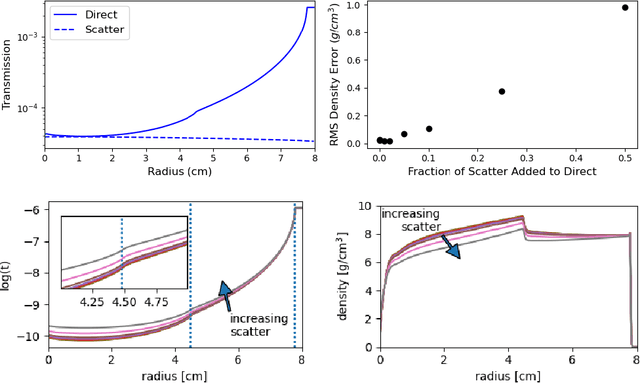
Radiography is often used to probe complex, evolving density fields in dynamic systems and in so doing gain insight into the underlying physics. This technique has been used in numerous fields including materials science, shock physics, inertial confinement fusion, and other national security applications. In many of these applications, however, complications resulting from noise, scatter, complex beam dynamics, etc. prevent the reconstruction of density from being accurate enough to identify the underlying physics with sufficient confidence. As such, density reconstruction from static/dynamic radiography has typically been limited to identifying discontinuous features such as cracks and voids in a number of these applications. In this work, we propose a fundamentally new approach to reconstructing density from a temporal sequence of radiographic images. Using only the robust features identifiable in radiographs, we combine them with the underlying hydrodynamic equations of motion using a machine learning approach, namely, conditional generative adversarial networks (cGAN), to determine the density fields from a dynamic sequence of radiographs. Next, we seek to further enhance the hydrodynamic consistency of the ML-based density reconstruction through a process of parameter estimation and projection onto a hydrodynamic manifold. In this context, we note that the distance from the hydrodynamic manifold given by the training data to the test data in the parameter space considered both serves as a diagnostic of the robustness of the predictions and serves to augment the training database, with the expectation that the latter will further reduce future density reconstruction errors. Finally, we demonstrate the ability of this method to outperform a traditional radiographic reconstruction in capturing allowable hydrodynamic paths even when relatively small amounts of scatter are present.

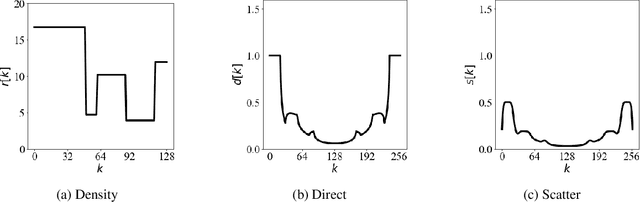
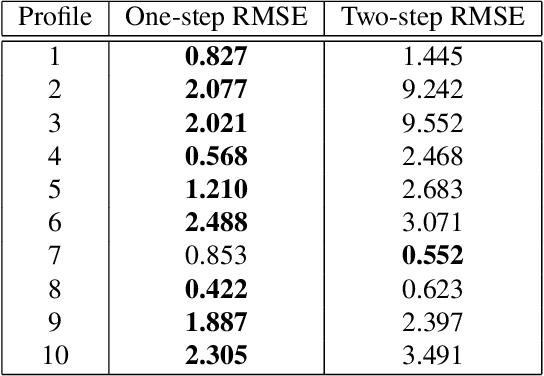
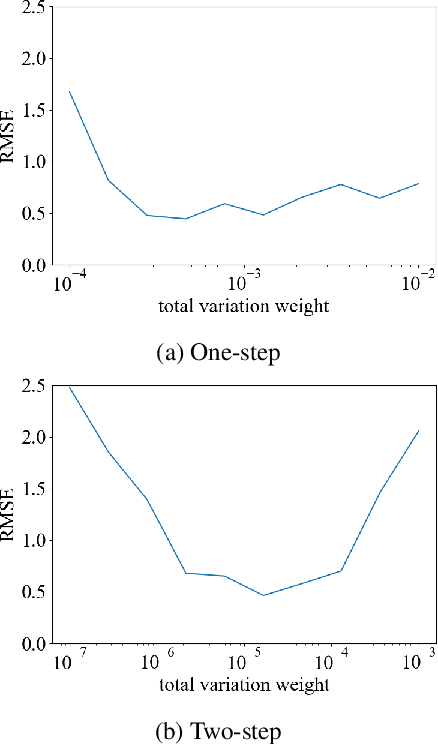
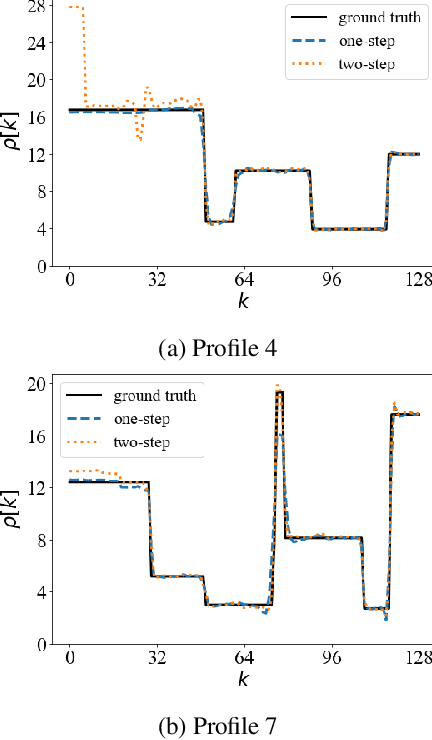
Comparing One-step and Two-step Scatter Correction and Density Reconstruction in X-ray CT

In this work, we compare one-step and two-step approaches for X-ray computed tomography (CT) scatter correction and density reconstruction. X-ray CT is an important imaging technique in medical and industrial applications. In many cases, the presence of scattered X-rays leads to loss of contrast and undesirable artifacts in reconstructed images. Many approaches to computationally removing scatter treat scatter correction as a preprocessing step that is followed by a reconstruction step. Treating scatter correction and reconstruction jointly as a single, more complicated optimization problem is less studied. It is not clear from the existing literature how these two approaches compare in terms of reconstruction accuracy. In this paper, we compare idealized versions of these two approaches with synthetic experiments. Our results show that the one-step approach can offer improved reconstructions over the two-step approach, although the gap between them is highly object-dependent.