Coarse-Graining Hamiltonian Systems Using WSINDy

The Weak-form Sparse Identification of Nonlinear Dynamics algorithm (WSINDy) has been demonstrated to offer coarse-graining capabilities in the context of interacting particle systems ( https://doi.org/10.1016/j.physd.2022.133406 ). In this work we extend this capability to the problem of coarse-graining Hamiltonian dynamics which possess approximate symmetries. Such approximate symmetries often lead to the existence of a Hamiltonian system of reduced dimension that may be used to efficiently capture the dynamics of the relevant degrees of freedom. Deriving such reduced systems, or approximating them numerically, is an ongoing challenge. We demonstrate that WSINDy can successfully identify this reduced Hamiltonian system in the presence of large perturbations imparted from both the inexact nature of the symmetry and extrinsic noise. This is significant in part due to the nontrivial means by which such systems are derived analytically. WSINDy naturally preserves the Hamiltonian structure by restricting to a trial basis of Hamiltonian vector fields, and the methodology is computational efficient, often requiring only a single trajectory to learn the full reduced Hamiltonian, and avoiding forward solves in the learning process. In this way, we argue that weak-form equation learning is particularly well-suited for Hamiltonian coarse-graining. Using nearly-periodic Hamiltonian systems as a prototypical class of systems with approximate symmetries, we show that WSINDy robustly identifies the correct leading-order reduced system of dimension $2(N-1)$ or $N$ from the original $(2N)$-dimensional system, upon observation of the relevant degrees of freedom. We provide physically relevant examples, namely coupled oscillator dynamics, the H\'enon-Heiles system for stellar motion within a galaxy, and the dynamics of charged particles.

Approximation of nearly-periodic symplectic maps via structure-preserving neural networks

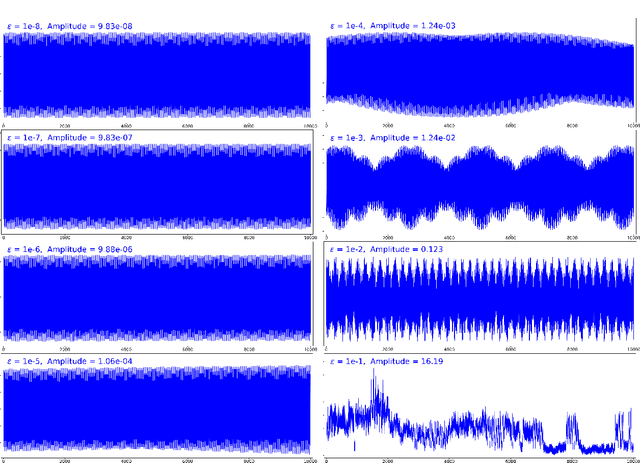
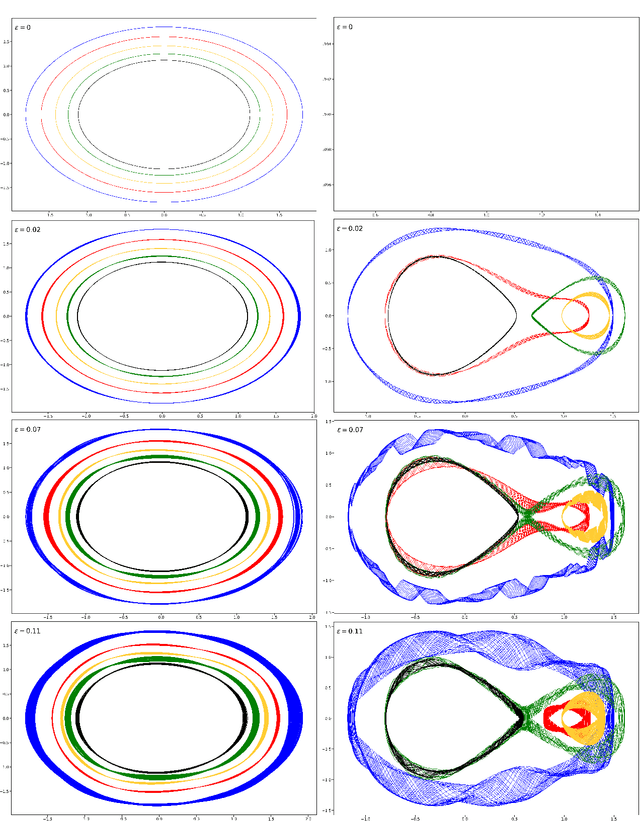
A continuous-time dynamical system with parameter $\varepsilon$ is nearly-periodic if all its trajectories are periodic with nowhere-vanishing angular frequency as $\varepsilon$ approaches 0. Nearly-periodic maps are discrete-time analogues of nearly-periodic systems, defined as parameter-dependent diffeomorphisms that limit to rotations along a circle action, and they admit formal $U(1)$ symmetries to all orders when the limiting rotation is non-resonant. For Hamiltonian nearly-periodic maps on exact presymplectic manifolds, the formal $U(1)$ symmetry gives rise to a discrete-time adiabatic invariant. In this paper, we construct a novel structure-preserving neural network to approximate nearly-periodic symplectic maps. This neural network architecture, which we call symplectic gyroceptron, ensures that the resulting surrogate map is nearly-periodic and symplectic, and that it gives rise to a discrete-time adiabatic invariant and a long-time stability. This new structure-preserving neural network provides a promising architecture for surrogate modeling of non-dissipative dynamical systems that automatically steps over short timescales without introducing spurious instabilities.

High-Precision Inversion of Dynamic Radiography Using Hydrodynamic Features

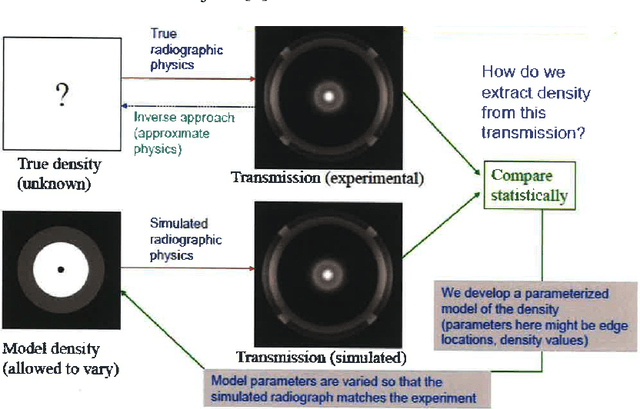
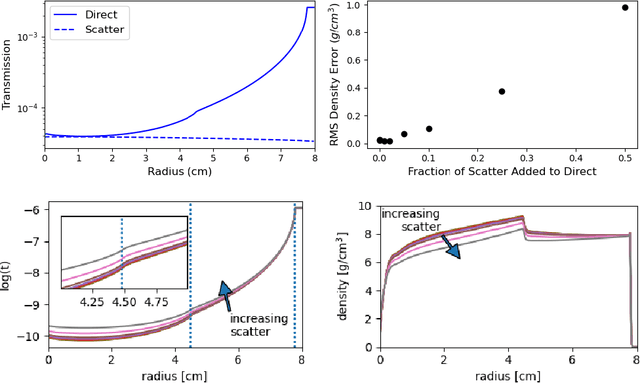
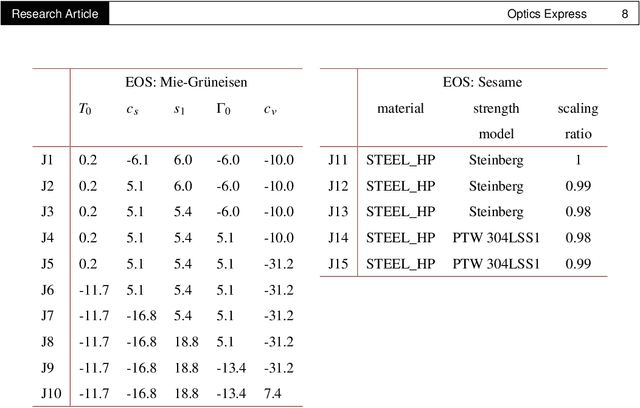
Radiography is often used to probe complex, evolving density fields in dynamic systems and in so doing gain insight into the underlying physics. This technique has been used in numerous fields including materials science, shock physics, inertial confinement fusion, and other national security applications. In many of these applications, however, complications resulting from noise, scatter, complex beam dynamics, etc. prevent the reconstruction of density from being accurate enough to identify the underlying physics with sufficient confidence. As such, density reconstruction from static/dynamic radiography has typically been limited to identifying discontinuous features such as cracks and voids in a number of these applications. In this work, we propose a fundamentally new approach to reconstructing density from a temporal sequence of radiographic images. Using only the robust features identifiable in radiographs, we combine them with the underlying hydrodynamic equations of motion using a machine learning approach, namely, conditional generative adversarial networks (cGAN), to determine the density fields from a dynamic sequence of radiographs. Next, we seek to further enhance the hydrodynamic consistency of the ML-based density reconstruction through a process of parameter estimation and projection onto a hydrodynamic manifold. In this context, we note that the distance from the hydrodynamic manifold given by the training data to the test data in the parameter space considered both serves as a diagnostic of the robustness of the predictions and serves to augment the training database, with the expectation that the latter will further reduce future density reconstruction errors. Finally, we demonstrate the ability of this method to outperform a traditional radiographic reconstruction in capturing allowable hydrodynamic paths even when relatively small amounts of scatter are present.