Learning physical unknowns from hydrodynamic shock and material interface features in ICF capsule implosions

In high energy density physics (HEDP) and inertial confinement fusion (ICF), predictive modeling is complicated by uncertainty in parameters that characterize various aspects of the modeled system, such as those characterizing material properties, equation of state (EOS), opacities, and initial conditions. Typically, however, these parameters are not directly observable. What is observed instead is a time sequence of radiographic projections using X-rays. In this work, we define a set of sparse hydrodynamic features derived from the outgoing shock profile and outer material edge, which can be obtained from radiographic measurements, to directly infer such parameters. Our machine learning (ML)-based methodology involves a pipeline of two architectures, a radiograph-to-features network (R2FNet) and a features-to-parameters network (F2PNet), that are trained independently and later combined to approximate a posterior distribution for the parameters from radiographs. We show that the estimated parameters can be used in a hydrodynamics code to obtain density fields and hydrodynamic shock and outer edge features that are consistent with the data. Finally, we demonstrate that features resulting from an unknown EOS model can be successfully mapped onto parameters of a chosen analytical EOS model, implying that network predictions are learning physics, with a degree of invariance to the underlying choice of EOS model.

Improving Radiography Machine Learning Workflows via Metadata Management for Training Data Selection

Most machine learning models require many iterations of hyper-parameter tuning, feature engineering, and debugging to produce effective results. As machine learning models become more complicated, this pipeline becomes more difficult to manage effectively. In the physical sciences, there is an ever-increasing pool of metadata that is generated by the scientific research cycle. Tracking this metadata can reduce redundant work, improve reproducibility, and aid in the feature and training dataset engineering process. In this case study, we present a tool for machine learning metadata management in dynamic radiography. We evaluate the efficacy of this tool against the initial research workflow and discuss extensions to general machine learning pipelines in the physical sciences.

High-Precision Inversion of Dynamic Radiography Using Hydrodynamic Features

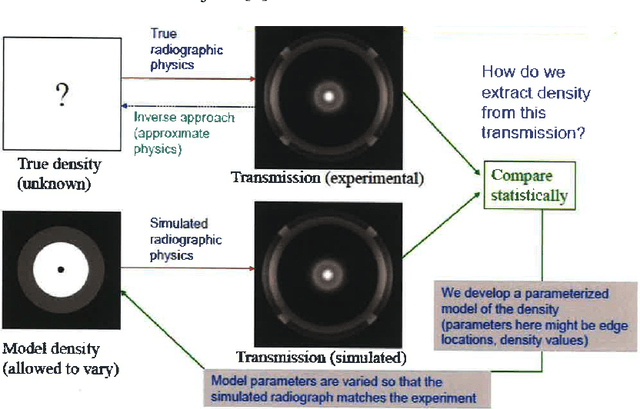
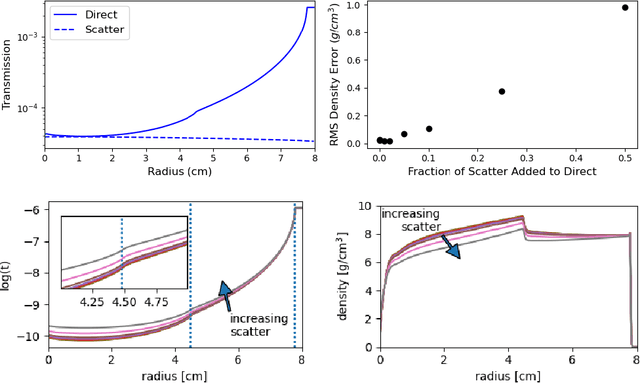
Radiography is often used to probe complex, evolving density fields in dynamic systems and in so doing gain insight into the underlying physics. This technique has been used in numerous fields including materials science, shock physics, inertial confinement fusion, and other national security applications. In many of these applications, however, complications resulting from noise, scatter, complex beam dynamics, etc. prevent the reconstruction of density from being accurate enough to identify the underlying physics with sufficient confidence. As such, density reconstruction from static/dynamic radiography has typically been limited to identifying discontinuous features such as cracks and voids in a number of these applications. In this work, we propose a fundamentally new approach to reconstructing density from a temporal sequence of radiographic images. Using only the robust features identifiable in radiographs, we combine them with the underlying hydrodynamic equations of motion using a machine learning approach, namely, conditional generative adversarial networks (cGAN), to determine the density fields from a dynamic sequence of radiographs. Next, we seek to further enhance the hydrodynamic consistency of the ML-based density reconstruction through a process of parameter estimation and projection onto a hydrodynamic manifold. In this context, we note that the distance from the hydrodynamic manifold given by the training data to the test data in the parameter space considered both serves as a diagnostic of the robustness of the predictions and serves to augment the training database, with the expectation that the latter will further reduce future density reconstruction errors. Finally, we demonstrate the ability of this method to outperform a traditional radiographic reconstruction in capturing allowable hydrodynamic paths even when relatively small amounts of scatter are present.