Projected Neural Differential Equations for Learning Constrained Dynamics

Neural differential equations offer a powerful approach for learning dynamics from data. However, they do not impose known constraints that should be obeyed by the learned model. It is well-known that enforcing constraints in surrogate models can enhance their generalizability and numerical stability. In this paper, we introduce projected neural differential equations (PNDEs), a new method for constraining neural differential equations based on projection of the learned vector field to the tangent space of the constraint manifold. In tests on several challenging examples, including chaotic dynamical systems and state-of-the-art power grid models, PNDEs outperform existing methods while requiring fewer hyperparameters. The proposed approach demonstrates significant potential for enhancing the modeling of constrained dynamical systems, particularly in complex domains where accuracy and reliability are essential.

An Operator Learning Framework for Spatiotemporal Super-resolution of Scientific Simulations

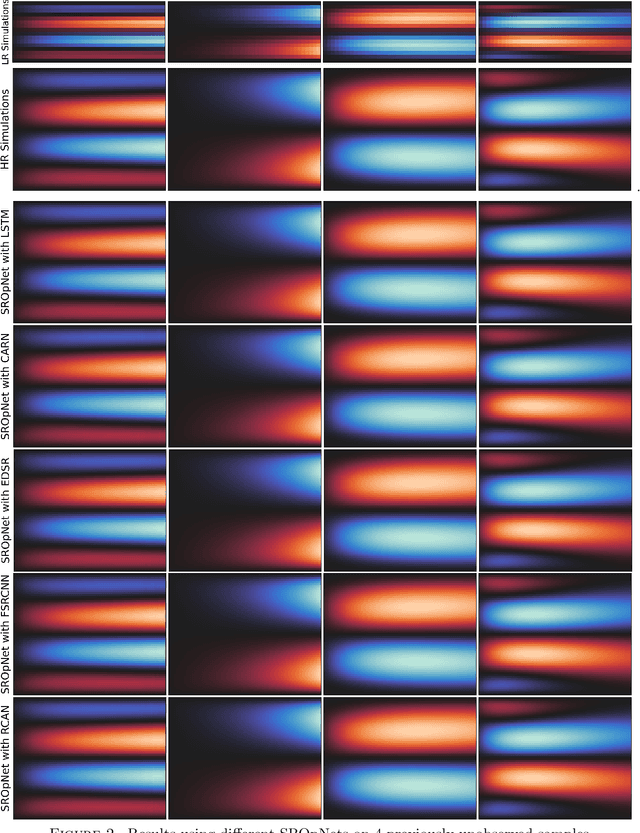
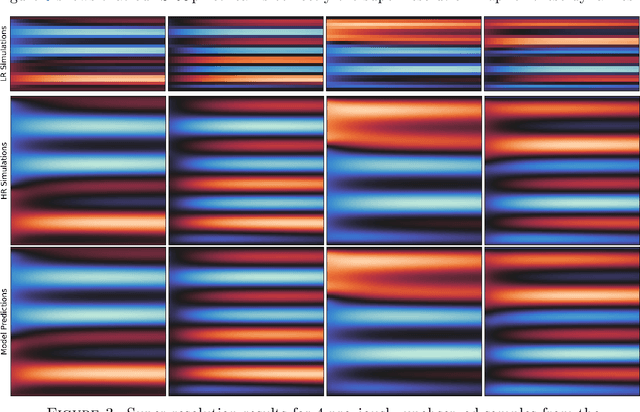
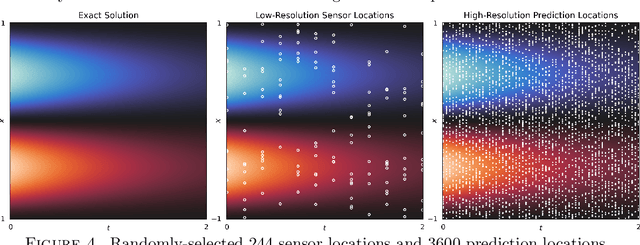
In numerous contexts, high-resolution solutions to partial differential equations are required to capture faithfully essential dynamics which occur at small spatiotemporal scales, but these solutions can be very difficult and slow to obtain using traditional methods due to limited computational resources. A recent direction to circumvent these computational limitations is to use machine learning techniques for super-resolution, to reconstruct high-resolution numerical solutions from low-resolution simulations which can be obtained more efficiently. The proposed approach, the Super Resolution Operator Network (SROpNet), frames super-resolution as an operator learning problem and draws inspiration from existing architectures to learn continuous representations of solutions to parametric differential equations from low-resolution approximations, which can then be evaluated at any desired location. In addition, no restrictions are imposed on the locations of (the fixed number of) spatiotemporal sensors at which the low-resolution approximations are provided, thereby enabling the consideration of a broader spectrum of problems arising in practice, for which many existing super-resolution approaches are not well-suited.

Simplifying Momentum-based Riemannian Submanifold Optimization

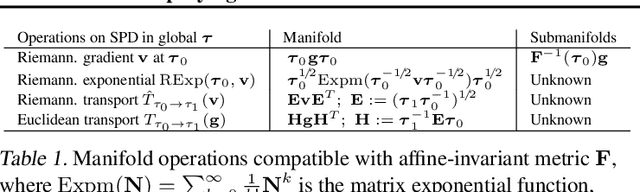
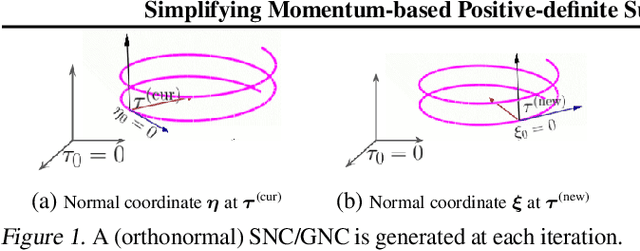
Riemannian submanifold optimization with momentum is computationally challenging because ensuring iterates remain on the submanifold often requires solving difficult differential equations. We simplify such optimization algorithms for the submanifold of symmetric positive-definite matrices with the affine invariant metric. We propose a generalized version of the Riemannian normal coordinates which dynamically trivializes the problem into a Euclidean unconstrained problem. We use our approach to explain and simplify existing approaches for structured covariances and develop efficient second-order optimizers for deep learning without explicit matrix inverses.

Lie Group Forced Variational Integrator Networks for Learning and Control of Robot Systems

Incorporating prior knowledge of physics laws and structural properties of dynamical systems into the design of deep learning architectures has proven to be a powerful technique for improving their computational efficiency and generalization capacity. Learning accurate models of robot dynamics is critical for safe and stable control. Autonomous mobile robots, including wheeled, aerial, and underwater vehicles, can be modeled as controlled Lagrangian or Hamiltonian rigid-body systems evolving on matrix Lie groups. In this paper, we introduce a new structure-preserving deep learning architecture, the Lie group Forced Variational Integrator Network (LieFVIN), capable of learning controlled Lagrangian or Hamiltonian dynamics on Lie groups, either from position-velocity or position-only data. By design, LieFVINs preserve both the Lie group structure on which the dynamics evolve and the symplectic structure underlying the Hamiltonian or Lagrangian systems of interest. The proposed architecture learns surrogate discrete-time flow maps allowing accurate and fast prediction without numerical-integrator, neural-ODE, or adjoint techniques, which are needed for vector fields. Furthermore, the learnt discrete-time dynamics can be utilized with computationally scalable discrete-time (optimal) control strategies.

Approximation of nearly-periodic symplectic maps via structure-preserving neural networks

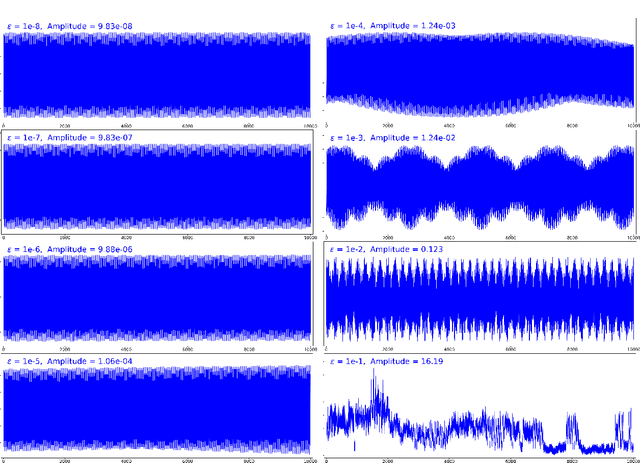
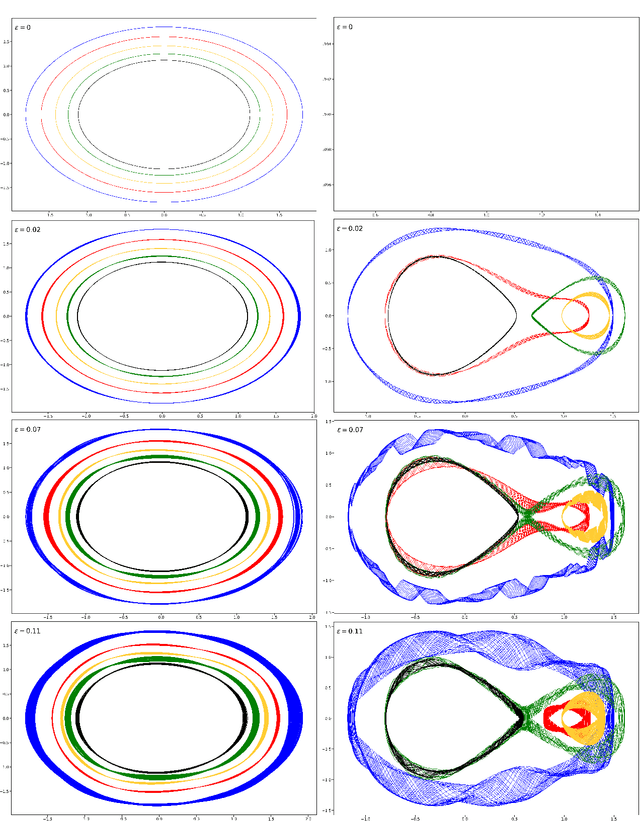
A continuous-time dynamical system with parameter $\varepsilon$ is nearly-periodic if all its trajectories are periodic with nowhere-vanishing angular frequency as $\varepsilon$ approaches 0. Nearly-periodic maps are discrete-time analogues of nearly-periodic systems, defined as parameter-dependent diffeomorphisms that limit to rotations along a circle action, and they admit formal $U(1)$ symmetries to all orders when the limiting rotation is non-resonant. For Hamiltonian nearly-periodic maps on exact presymplectic manifolds, the formal $U(1)$ symmetry gives rise to a discrete-time adiabatic invariant. In this paper, we construct a novel structure-preserving neural network to approximate nearly-periodic symplectic maps. This neural network architecture, which we call symplectic gyroceptron, ensures that the resulting surrogate map is nearly-periodic and symplectic, and that it gives rise to a discrete-time adiabatic invariant and a long-time stability. This new structure-preserving neural network provides a promising architecture for surrogate modeling of non-dissipative dynamical systems that automatically steps over short timescales without introducing spurious instabilities.