Decadal sink-source shifts of forest aboveground carbon since 1988

As enduring carbon sinks, forest ecosystems are vital to the terrestrial carbon cycle and help moderate global warming. However, the long-term dynamics of aboveground carbon (AGC) in forests and their sink-source transitions remain highly uncertain, owing to changing disturbance regimes and inconsistencies in observations, data processing, and analysis methods. Here, we derive reliable, harmonized AGC stocks and fluxes in global forests from 1988 to 2021 at high spatial resolution by integrating multi-source satellite observations with probabilistic deep learning models. Our approach simultaneously estimates AGC and associated uncertainties, showing high reliability across space and time. We find that, although global forests remained an AGC sink of 6.2 PgC over 30 years, moist tropical forests shifted to a substantial AGC source between 2001 and 2010 and, together with boreal forests, transitioned toward a source in the 2011-2021 period. Temperate, dry tropical and subtropical forests generally exhibited increasing AGC stocks, although Europe and Australia became sources after 2011. Regionally, pronounced sink-to-source transitions occurred in tropical forests over the past three decades. The interannual relationship between global atmospheric CO2 growth rates and tropical AGC flux variability became increasingly negative, reaching Pearson's r = -0.63 (p < 0.05) in the most recent decade. In the Brazilian Amazon, the contribution of deforested regions to AGC losses declined from 60% in 1989-2000 to 13% in 2011-2021, while the share from untouched areas increased from 33% to 76%. Our findings suggest a growing role of tropical forest AGC in modulating variability in the terrestrial carbon cycle, with anthropogenic climate change potentially contributing increasingly to AGC changes, particularly in previously untouched areas.

Generating time-consistent dynamics with discriminator-guided image diffusion models

Realistic temporal dynamics are crucial for many video generation, processing and modelling applications, e.g. in computational fluid dynamics, weather prediction, or long-term climate simulations. Video diffusion models (VDMs) are the current state-of-the-art method for generating highly realistic dynamics. However, training VDMs from scratch can be challenging and requires large computational resources, limiting their wider application. Here, we propose a time-consistency discriminator that enables pretrained image diffusion models to generate realistic spatiotemporal dynamics. The discriminator guides the sampling inference process and does not require extensions or finetuning of the image diffusion model. We compare our approach against a VDM trained from scratch on an idealized turbulence simulation and a real-world global precipitation dataset. Our approach performs equally well in terms of temporal consistency, shows improved uncertainty calibration and lower biases compared to the VDM, and achieves stable centennial-scale climate simulations at daily time steps.

Generative assimilation and prediction for weather and climate

Machine learning models have shown great success in predicting weather up to two weeks ahead, outperforming process-based benchmarks. However, existing approaches mostly focus on the prediction task, and do not incorporate the necessary data assimilation. Moreover, these models suffer from error accumulation in long roll-outs, limiting their applicability to seasonal predictions or climate projections. Here, we introduce Generative Assimilation and Prediction (GAP), a unified deep generative framework for assimilation and prediction of both weather and climate. By learning to quantify the probabilistic distribution of atmospheric states under observational, predictive, and external forcing constraints, GAP excels in a broad range of weather-climate related tasks, including data assimilation, seamless prediction, and climate simulation. In particular, GAP is competitive with state-of-the-art ensemble assimilation, probabilistic weather forecast and seasonal prediction, yields stable millennial simulations, and reproduces climate variability from daily to decadal time scales.

Improving the Noise Estimation of Latent Neural Stochastic Differential Equations

Latent neural stochastic differential equations (SDEs) have recently emerged as a promising approach for learning generative models from stochastic time series data. However, they systematically underestimate the noise level inherent in such data, limiting their ability to capture stochastic dynamics accurately. We investigate this underestimation in detail and propose a straightforward solution: by including an explicit additional noise regularization in the loss function, we are able to learn a model that accurately captures the diffusion component of the data. We demonstrate our results on a conceptual model system that highlights the improved latent neural SDE's capability to model stochastic bistable dynamics.

Projected Neural Differential Equations for Learning Constrained Dynamics

Neural differential equations offer a powerful approach for learning dynamics from data. However, they do not impose known constraints that should be obeyed by the learned model. It is well-known that enforcing constraints in surrogate models can enhance their generalizability and numerical stability. In this paper, we introduce projected neural differential equations (PNDEs), a new method for constraining neural differential equations based on projection of the learned vector field to the tangent space of the constraint manifold. In tests on several challenging examples, including chaotic dynamical systems and state-of-the-art power grid models, PNDEs outperform existing methods while requiring fewer hyperparameters. The proposed approach demonstrates significant potential for enhancing the modeling of constrained dynamical systems, particularly in complex domains where accuracy and reliability are essential.

Deep Learning for predicting rate-induced tipping

Nonlinear dynamical systems exposed to changing forcing can exhibit catastrophic transitions between alternative and often markedly different states. The phenomenon of critical slowing down (CSD) can be used to anticipate such transitions if caused by a bifurcation and if the change in forcing is slow compared to the internal time scale of the system. However, in many real-world situations, these assumptions are not met and transitions can be triggered because the forcing exceeds a critical rate. For example, given the pace of anthropogenic climate change in comparison to the internal time scales of key Earth system components, such as the polar ice sheets or the Atlantic Meridional Overturning Circulation, such rate-induced tipping poses a severe risk. Moreover, depending on the realisation of random perturbations, some trajectories may transition across an unstable boundary, while others do not, even under the same forcing. CSD-based indicators generally cannot distinguish these cases of noise-induced tipping versus no tipping. This severely limits our ability to assess the risks of tipping, and to predict individual trajectories. To address this, we make a first attempt to develop a deep learning framework to predict transition probabilities of dynamical systems ahead of rate-induced transitions. Our method issues early warnings, as demonstrated on three prototypical systems for rate-induced tipping, subjected to time-varying equilibrium drift and noise perturbations. Exploiting explainable artificial intelligence methods, our framework captures the fingerprints necessary for early detection of rate-induced tipping, even in cases of long lead times. Our findings demonstrate the predictability of rate-induced and noise-induced tipping, advancing our ability to determine safe operating spaces for a broader class of dynamical systems than possible so far.

Machine Learning for predicting chaotic systems

Predicting chaotic dynamical systems is critical in many scientific fields such as weather prediction, but challenging due to the characterizing sensitive dependence on initial conditions. Traditional modeling approaches require extensive domain knowledge, often leading to a shift towards data-driven methods using machine learning. However, existing research provides inconclusive results on which machine learning methods are best suited for predicting chaotic systems. In this paper, we compare different lightweight and heavyweight machine learning architectures using extensive existing databases, as well as a newly introduced one that allows for uncertainty quantification in the benchmark results. We perform hyperparameter tuning based on computational cost and introduce a novel error metric, the cumulative maximum error, which combines several desirable properties of traditional metrics, tailored for chaotic systems. Our results show that well-tuned simple methods, as well as untuned baseline methods, often outperform state-of-the-art deep learning models, but their performance can vary significantly with different experimental setups. These findings underscore the importance of matching prediction methods to data characteristics and available computational resources.

ORCA: A Global Ocean Emulator for Multi-year to Decadal Predictions

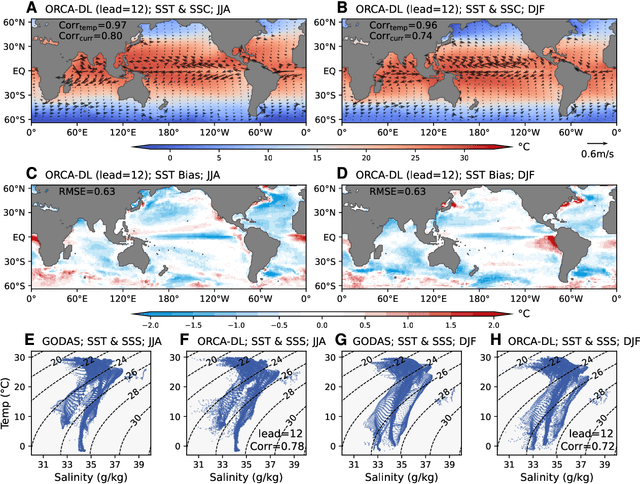
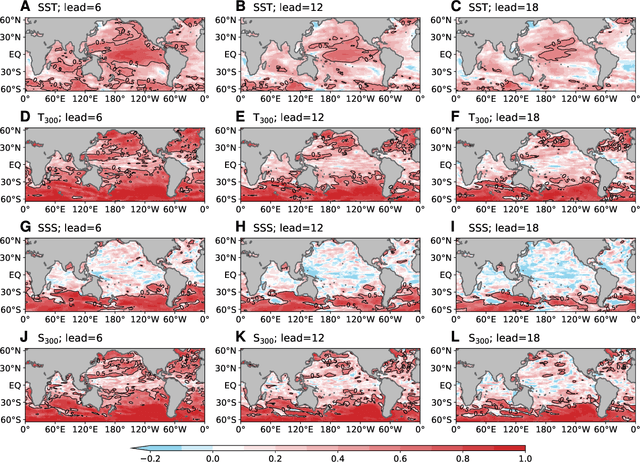
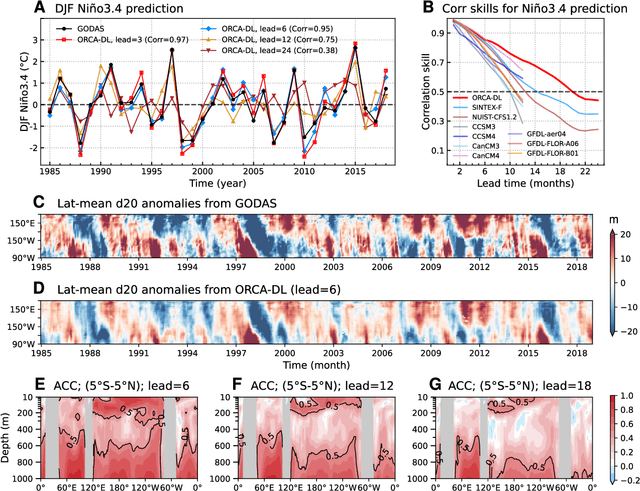
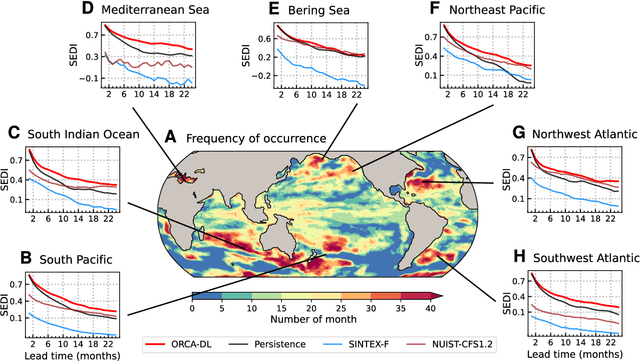
Ocean dynamics plays a crucial role in driving global weather and climate patterns. Accurate and efficient modeling of ocean dynamics is essential for improved understanding of complex ocean circulation and processes, for predicting climate variations and their associated teleconnections, and for addressing the challenges of climate change. While great efforts have been made to improve numerical Ocean General Circulation Models (OGCMs), accurate forecasting of global oceanic variations for multi-year remains to be a long-standing challenge. Here, we introduce ORCA (Oceanic Reliable foreCAst), the first data-driven model predicting global ocean circulation from multi-year to decadal time scales. ORCA accurately simulates the three-dimensional circulations and dynamics of the global ocean with high physical consistency. Hindcasts of key oceanic variables demonstrate ORCA's remarkable prediction skills in predicting ocean variations compared with state-of-the-art numerical OGCMs and abilities in capturing occurrences of extreme events at the subsurface ocean and ENSO vertical patterns. These results demonstrate the potential of data-driven ocean models for providing cheap, efficient, and accurate global ocean modeling and prediction. Moreover, ORCA stably and faithfully emulates ocean dynamics at decadal timescales, demonstrating its potential even for climate projections. The model will be available at https://github.com/OpenEarthLab/ORCA.

Fast, Scale-Adaptive, and Uncertainty-Aware Downscaling of Earth System Model Fields with Generative Foundation Models

Accurate and high-resolution Earth system model (ESM) simulations are essential to assess the ecological and socio-economic impacts of anthropogenic climate change, but are computationally too expensive. Recent machine learning approaches have shown promising results in downscaling ESM simulations, outperforming state-of-the-art statistical approaches. However, existing methods require computationally costly retraining for each ESM and extrapolate poorly to climates unseen during training. We address these shortcomings by learning a consistency model (CM) that efficiently and accurately downscales arbitrary ESM simulations without retraining in a zero-shot manner. Our foundation model approach yields probabilistic downscaled fields at resolution only limited by the observational reference data. We show that the CM outperforms state-of-the-art diffusion models at a fraction of computational cost while maintaining high controllability on the downscaling task. Further, our method generalizes to climate states unseen during training without explicitly formulated physical constraints.

ResoNet: Robust and Explainable ENSO Forecasts with Hybrid Convolution and Transformer Networks

Recent studies have shown that deep learning (DL) models can skillfully predict the El Ni\~no-Southern Oscillation (ENSO) forecasts over 1.5 years ahead. However, concerns regarding the reliability of predictions made by DL methods persist, including potential overfitting issues and lack of interpretability. Here, we propose ResoNet, a DL model that combines convolutional neural network (CNN) and Transformer architectures. This hybrid architecture design enables our model to adequately capture local SSTA as well as long-range inter-basin interactions across oceans. We show that ResoNet can robustly predict ESNO at lead times between 19 and 26 months, thus outperforming existing approaches in terms of the forecast horizon. According to an explainability method applied to ResoNet predictions of El Ni\~no and La Ni\~na events from 1- to 18-month lead, we find that it predicts the Ni\~no3.4 index based on multiple physically reasonable mechanisms, such as the Recharge Oscillator concept, Seasonal Footprint Mechanism, and Indian Ocean capacitor effect. Moreover, we demonstrate that for the first time, the asymmetry between El Ni\~no and La Ni\~na development can be captured by ResoNet. Our results could help alleviate skepticism about applying DL models for ENSO prediction and encourage more attempts to discover and predict climate phenomena using AI methods.