Generative Intervention Models for Causal Perturbation Modeling

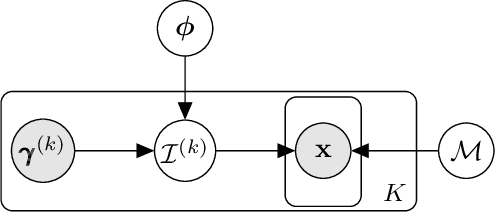
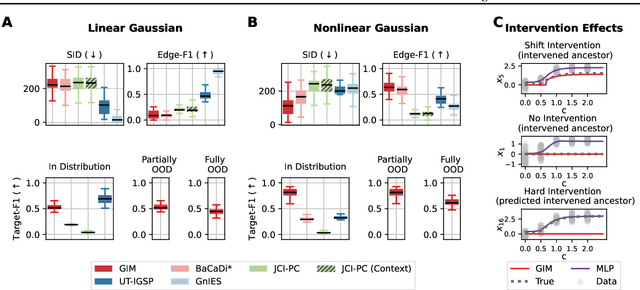
We consider the problem of predicting perturbation effects via causal models. In many applications, it is a priori unknown which mechanisms of a system are modified by an external perturbation, even though the features of the perturbation are available. For example, in genomics, some properties of a drug may be known, but not their causal effects on the regulatory pathways of cells. We propose a generative intervention model (GIM) that learns to map these perturbation features to distributions over atomic interventions in a jointly-estimated causal model. Contrary to prior approaches, this enables us to predict the distribution shifts of unseen perturbation features while gaining insights about their mechanistic effects in the underlying data-generating process. On synthetic data and scRNA-seq drug perturbation data, GIMs achieve robust out-of-distribution predictions on par with unstructured approaches, while effectively inferring the underlying perturbation mechanisms, often better than other causal inference methods.

Projected Neural Differential Equations for Learning Constrained Dynamics

Neural differential equations offer a powerful approach for learning dynamics from data. However, they do not impose known constraints that should be obeyed by the learned model. It is well-known that enforcing constraints in surrogate models can enhance their generalizability and numerical stability. In this paper, we introduce projected neural differential equations (PNDEs), a new method for constraining neural differential equations based on projection of the learned vector field to the tangent space of the constraint manifold. In tests on several challenging examples, including chaotic dynamical systems and state-of-the-art power grid models, PNDEs outperform existing methods while requiring fewer hyperparameters. The proposed approach demonstrates significant potential for enhancing the modeling of constrained dynamical systems, particularly in complex domains where accuracy and reliability are essential.

Uncertainty-Aware Optimal Treatment Selection for Clinical Time Series

In personalized medicine, the ability to predict and optimize treatment outcomes across various time frames is essential. Additionally, the ability to select cost-effective treatments within specific budget constraints is critical. Despite recent advancements in estimating counterfactual trajectories, a direct link to optimal treatment selection based on these estimates is missing. This paper introduces a novel method integrating counterfactual estimation techniques and uncertainty quantification to recommend personalized treatment plans adhering to predefined cost constraints. Our approach is distinctive in its handling of continuous treatment variables and its incorporation of uncertainty quantification to improve prediction reliability. We validate our method using two simulated datasets, one focused on the cardiovascular system and the other on COVID-19. Our findings indicate that our method has robust performance across different counterfactual estimation baselines, showing that introducing uncertainty quantification in these settings helps the current baselines in finding more reliable and accurate treatment selection. The robustness of our method across various settings highlights its potential for broad applicability in personalized healthcare solutions.

Learning Representations of Instruments for Partial Identification of Treatment Effects

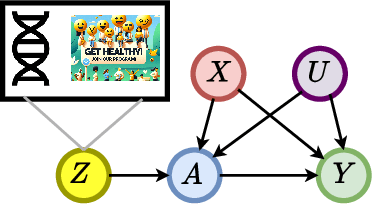
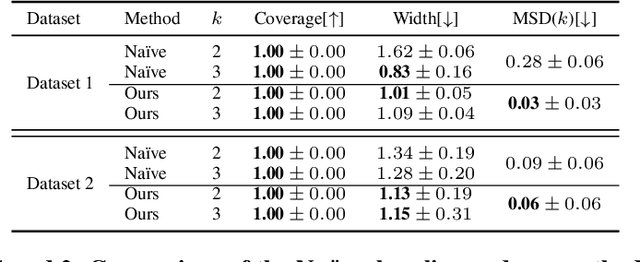
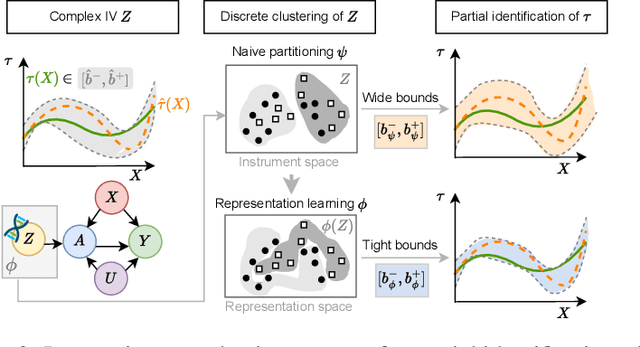
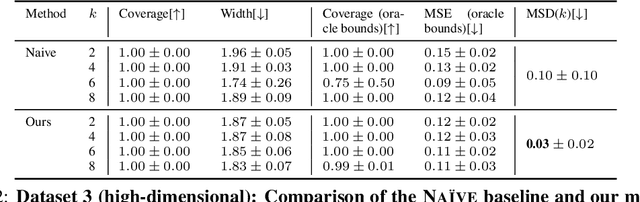
Reliable estimation of treatment effects from observational data is important in many disciplines such as medicine. However, estimation is challenging when unconfoundedness as a standard assumption in the causal inference literature is violated. In this work, we leverage arbitrary (potentially high-dimensional) instruments to estimate bounds on the conditional average treatment effect (CATE). Our contributions are three-fold: (1) We propose a novel approach for partial identification through a mapping of instruments to a discrete representation space so that we yield valid bounds on the CATE. This is crucial for reliable decision-making in real-world applications. (2) We derive a two-step procedure that learns tight bounds using a tailored neural partitioning of the latent instrument space. As a result, we avoid instability issues due to numerical approximations or adversarial training. Furthermore, our procedure aims to reduce the estimation variance in finite-sample settings to yield more reliable estimates. (3) We show theoretically that our procedure obtains valid bounds while reducing estimation variance. We further perform extensive experiments to demonstrate the effectiveness across various settings. Overall, our procedure offers a novel path for practitioners to make use of potentially high-dimensional instruments (e.g., as in Mendelian randomization).

Causal machine learning for predicting treatment outcomes

Causal machine learning (ML) offers flexible, data-driven methods for predicting treatment outcomes including efficacy and toxicity, thereby supporting the assessment and safety of drugs. A key benefit of causal ML is that it allows for estimating individualized treatment effects, so that clinical decision-making can be personalized to individual patient profiles. Causal ML can be used in combination with both clinical trial data and real-world data, such as clinical registries and electronic health records, but caution is needed to avoid biased or incorrect predictions. In this Perspective, we discuss the benefits of causal ML (relative to traditional statistical or ML approaches) and outline the key components and steps. Finally, we provide recommendations for the reliable use of causal ML and effective translation into the clinic.

Towards Physically Consistent Deep Learning For Climate Model Parameterizations

Climate models play a critical role in understanding and projecting climate change. Due to their complexity, their horizontal resolution of ~40-100 km remains too coarse to resolve processes such as clouds and convection, which need to be approximated via parameterizations. These parameterizations are a major source of systematic errors and large uncertainties in climate projections. Deep learning (DL)-based parameterizations, trained on computationally expensive, short high-resolution simulations, have shown great promise for improving climate models in that regard. However, their lack of interpretability and tendency to learn spurious non-physical correlations result in reduced trust in the climate simulation. We propose an efficient supervised learning framework for DL-based parameterizations that leads to physically consistent models with improved interpretability and negligible computational overhead compared to standard supervised training. First, key features determining the target physical processes are uncovered. Subsequently, the neural network is fine-tuned using only those relevant features. We show empirically that our method robustly identifies a small subset of the inputs as actual physical drivers, therefore, removing spurious non-physical relationships. This results in by design physically consistent and interpretable neural networks while maintaining the predictive performance of standard black-box DL-based parameterizations. Our framework represents a crucial step in addressing a major challenge in data-driven climate model parameterizations by respecting the underlying physical processes, and may also benefit physically consistent deep learning in other research fields.

Targeted Sequential Indirect Experiment Design

Scientific hypotheses typically concern specific aspects of complex, imperfectly understood or entirely unknown mechanisms, such as the effect of gene expression levels on phenotypes or how microbial communities influence environmental health. Such queries are inherently causal (rather than purely associational), but in many settings, experiments can not be conducted directly on the target variables of interest, but are indirect. Therefore, they perturb the target variable, but do not remove potential confounding factors. If, additionally, the resulting experimental measurements are multi-dimensional and the studied mechanisms nonlinear, the query of interest is generally not identified. We develop an adaptive strategy to design indirect experiments that optimally inform a targeted query about the ground truth mechanism in terms of sequentially narrowing the gap between an upper and lower bound on the query. While the general formulation consists of a bi-level optimization procedure, we derive an efficiently estimable analytical kernel-based estimator of the bounds for the causal effect, a query of key interest, and demonstrate the efficacy of our approach in confounded, multivariate, nonlinear synthetic settings.

Whole Genome Transformer for Gene Interaction Effects in Microbiome Habitat Specificity

Leveraging the vast genetic diversity within microbiomes offers unparalleled insights into complex phenotypes, yet the task of accurately predicting and understanding such traits from genomic data remains challenging. We propose a framework taking advantage of existing large models for gene vectorization to predict habitat specificity from entire microbial genome sequences. Based on our model, we develop attribution techniques to elucidate gene interaction effects that drive microbial adaptation to diverse environments. We train and validate our approach on a large dataset of high quality microbiome genomes from different habitats. We not only demonstrate solid predictive performance, but also how sequence-level information of entire genomes allows us to identify gene associations underlying complex phenotypes. Our attribution recovers known important interaction networks and proposes new candidates for experimental follow up.

Signature Kernel Conditional Independence Tests in Causal Discovery for Stochastic Processes

Inferring the causal structure underlying stochastic dynamical systems from observational data holds great promise in domains ranging from science and health to finance. Such processes can often be accurately modeled via stochastic differential equations (SDEs), which naturally imply causal relationships via "which variables enter the differential of which other variables". In this paper, we develop a kernel-based test of conditional independence (CI) on "path-space" -- solutions to SDEs -- by leveraging recent advances in signature kernels. We demonstrate strictly superior performance of our proposed CI test compared to existing approaches on path-space. Then, we develop constraint-based causal discovery algorithms for acyclic stochastic dynamical systems (allowing for loops) that leverage temporal information to recover the entire directed graph. Assuming faithfulness and a CI oracle, our algorithm is sound and complete. We empirically verify that our developed CI test in conjunction with the causal discovery algorithm reliably outperforms baselines across a range of settings.

Unbalancedness in Neural Monge Maps Improves Unpaired Domain Translation

In optimal transport (OT), a Monge map is known as a mapping that transports a source distribution to a target distribution in the most cost-efficient way. Recently, multiple neural estimators for Monge maps have been developed and applied in diverse unpaired domain translation tasks, e.g. in single-cell biology and computer vision. However, the classic OT framework enforces mass conservation, which makes it prone to outliers and limits its applicability in real-world scenarios. The latter can be particularly harmful in OT domain translation tasks, where the relative position of a sample within a distribution is explicitly taken into account. While unbalanced OT tackles this challenge in the discrete setting, its integration into neural Monge map estimators has received limited attention. We propose a theoretically grounded method to incorporate unbalancedness into any Monge map estimator. We improve existing estimators to model cell trajectories over time and to predict cellular responses to perturbations. Moreover, our approach seamlessly integrates with the OT flow matching (OT-FM) framework. While we show that OT-FM performs competitively in image translation, we further improve performance by incorporating unbalancedness (UOT-FM), which better preserves relevant features. We hence establish UOT-FM as a principled method for unpaired image translation.