Constructing Confidence Intervals for Average Treatment Effects from Multiple Datasets

Constructing confidence intervals (CIs) for the average treatment effect (ATE) from patient records is crucial to assess the effectiveness and safety of drugs. However, patient records typically come from different hospitals, thus raising the question of how multiple observational datasets can be effectively combined for this purpose. In our paper, we propose a new method that estimates the ATE from multiple observational datasets and provides valid CIs. Our method makes little assumptions about the observational datasets and is thus widely applicable in medical practice. The key idea of our method is that we leverage prediction-powered inferences and thereby essentially `shrink' the CIs so that we offer more precise uncertainty quantification as compared to na\"ive approaches. We further prove the unbiasedness of our method and the validity of our CIs. We confirm our theoretical results through various numerical experiments. Finally, we provide an extension of our method for constructing CIs from combinations of experimental and observational datasets.

Slowing Down Forgetting in Continual Learning

A common challenge in continual learning (CL) is catastrophic forgetting, where the performance on old tasks drops after new, additional tasks are learned. In this paper, we propose a novel framework called ReCL to slow down forgetting in CL. Our framework exploits an implicit bias of gradient-based neural networks due to which these converge to margin maximization points. Such convergence points allow us to reconstruct old data from previous tasks, which we then combine with the current training data. Our framework is flexible and can be applied on top of existing, state-of-the-art CL methods to slow down forgetting. We further demonstrate the performance gain from our framework across a large series of experiments, including different CL scenarios (class incremental, domain incremental, task incremental learning) different datasets (MNIST, CIFAR10), and different network architectures. Across all experiments, we find large performance gains through ReCL. To the best of our knowledge, our framework is the first to address catastrophic forgetting by leveraging models in CL as their own memory buffers.

Quantifying Aleatoric Uncertainty of the Treatment Effect: A Novel Orthogonal Learner

Estimating causal quantities from observational data is crucial for understanding the safety and effectiveness of medical treatments. However, to make reliable inferences, medical practitioners require not only estimating averaged causal quantities, such as the conditional average treatment effect, but also understanding the randomness of the treatment effect as a random variable. This randomness is referred to as aleatoric uncertainty and is necessary for understanding the probability of benefit from treatment or quantiles of the treatment effect. Yet, the aleatoric uncertainty of the treatment effect has received surprisingly little attention in the causal machine learning community. To fill this gap, we aim to quantify the aleatoric uncertainty of the treatment effect at the covariate-conditional level, namely, the conditional distribution of the treatment effect (CDTE). Unlike average causal quantities, the CDTE is not point identifiable without strong additional assumptions. As a remedy, we employ partial identification to obtain sharp bounds on the CDTE and thereby quantify the aleatoric uncertainty of the treatment effect. We then develop a novel, orthogonal learner for the bounds on the CDTE, which we call AU-learner. We further show that our AU-learner has several strengths in that it satisfies Neyman-orthogonality and is doubly robust. Finally, we propose a fully-parametric deep learning instantiation of our AU-learner.

DiffPO: A causal diffusion model for learning distributions of potential outcomes

Predicting potential outcomes of interventions from observational data is crucial for decision-making in medicine, but the task is challenging due to the fundamental problem of causal inference. Existing methods are largely limited to point estimates of potential outcomes with no uncertain quantification; thus, the full information about the distributions of potential outcomes is typically ignored. In this paper, we propose a novel causal diffusion model called DiffPO, which is carefully designed for reliable inferences in medicine by learning the distribution of potential outcomes. In our DiffPO, we leverage a tailored conditional denoising diffusion model to learn complex distributions, where we address the selection bias through a novel orthogonal diffusion loss. Another strength of our DiffPO method is that it is highly flexible (e.g., it can also be used to estimate different causal quantities such as CATE). Across a wide range of experiments, we show that our method achieves state-of-the-art performance.

Causal machine learning for predicting treatment outcomes

Causal machine learning (ML) offers flexible, data-driven methods for predicting treatment outcomes including efficacy and toxicity, thereby supporting the assessment and safety of drugs. A key benefit of causal ML is that it allows for estimating individualized treatment effects, so that clinical decision-making can be personalized to individual patient profiles. Causal ML can be used in combination with both clinical trial data and real-world data, such as clinical registries and electronic health records, but caution is needed to avoid biased or incorrect predictions. In this Perspective, we discuss the benefits of causal ML (relative to traditional statistical or ML approaches) and outline the key components and steps. Finally, we provide recommendations for the reliable use of causal ML and effective translation into the clinic.

Learning Representations of Instruments for Partial Identification of Treatment Effects

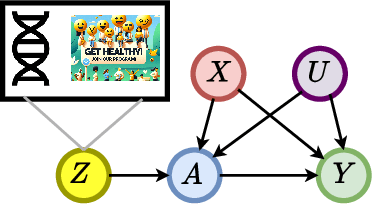
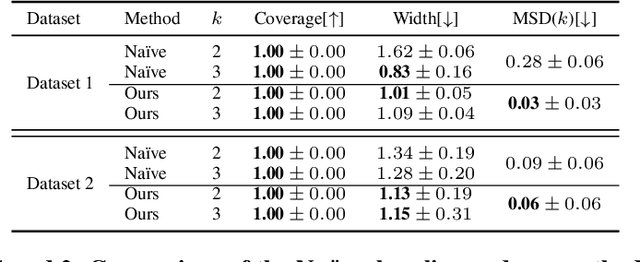
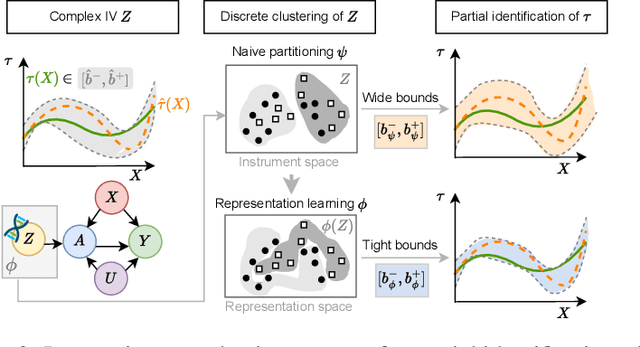
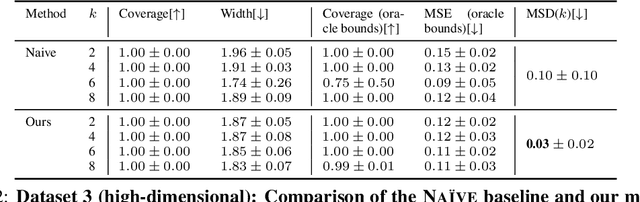
Reliable estimation of treatment effects from observational data is important in many disciplines such as medicine. However, estimation is challenging when unconfoundedness as a standard assumption in the causal inference literature is violated. In this work, we leverage arbitrary (potentially high-dimensional) instruments to estimate bounds on the conditional average treatment effect (CATE). Our contributions are three-fold: (1) We propose a novel approach for partial identification through a mapping of instruments to a discrete representation space so that we yield valid bounds on the CATE. This is crucial for reliable decision-making in real-world applications. (2) We derive a two-step procedure that learns tight bounds using a tailored neural partitioning of the latent instrument space. As a result, we avoid instability issues due to numerical approximations or adversarial training. Furthermore, our procedure aims to reduce the estimation variance in finite-sample settings to yield more reliable estimates. (3) We show theoretically that our procedure obtains valid bounds while reducing estimation variance. We further perform extensive experiments to demonstrate the effectiveness across various settings. Overall, our procedure offers a novel path for practitioners to make use of potentially high-dimensional instruments (e.g., as in Mendelian randomization).

Stabilized Neural Prediction of Potential Outcomes in Continuous Time

Patient trajectories from electronic health records are widely used to predict potential outcomes of treatments over time, which then allows to personalize care. Yet, existing neural methods for this purpose have a key limitation: while some adjust for time-varying confounding, these methods assume that the time series are recorded in discrete time. In other words, they are constrained to settings where measurements and treatments are conducted at fixed time steps, even though this is unrealistic in medical practice. In this work, we aim to predict potential outcomes in continuous time. The latter is of direct practical relevance because it allows for modeling patient trajectories where measurements and treatments take place at arbitrary, irregular timestamps. We thus propose a new method called stabilized continuous time inverse propensity network (SCIP-Net). For this, we further derive stabilized inverse propensity weights for robust prediction of the potential outcomes. To the best of our knowledge, our SCIP-Net is the first neural method that performs proper adjustments for time-varying confounding in continuous time.

Automated Knowledge Concept Annotation and Question Representation Learning for Knowledge Tracing

Knowledge tracing (KT) is a popular approach for modeling students' learning progress over time, which can enable more personalized and adaptive learning. However, existing KT approaches face two major limitations: (1) they rely heavily on expert-defined knowledge concepts (KCs) in questions, which is time-consuming and prone to errors; and (2) KT methods tend to overlook the semantics of both questions and the given KCs. In this work, we address these challenges and present KCQRL, a framework for automated knowledge concept annotation and question representation learning that can improve the effectiveness of any existing KT model. First, we propose an automated KC annotation process using large language models (LLMs), which generates question solutions and then annotates KCs in each solution step of the questions. Second, we introduce a contrastive learning approach to generate semantically rich embeddings for questions and solution steps, aligning them with their associated KCs via a tailored false negative elimination approach. These embeddings can be readily integrated into existing KT models, replacing their randomly initialized embeddings. We demonstrate the effectiveness of KCQRL across 15 KT algorithms on two large real-world Math learning datasets, where we achieve consistent performance improvements.

A Fused Large Language Model for Predicting Startup Success

Investors are continuously seeking profitable investment opportunities in startups and, hence, for effective decision-making, need to predict a startup's probability of success. Nowadays, investors can use not only various fundamental information about a startup (e.g., the age of the startup, the number of founders, and the business sector) but also textual description of a startup's innovation and business model, which is widely available through online venture capital (VC) platforms such as Crunchbase. To support the decision-making of investors, we develop a machine learning approach with the aim of locating successful startups on VC platforms. Specifically, we develop, train, and evaluate a tailored, fused large language model to predict startup success. Thereby, we assess to what extent self-descriptions on VC platforms are predictive of startup success. Using 20,172 online profiles from Crunchbase, we find that our fused large language model can predict startup success, with textual self-descriptions being responsible for a significant part of the predictive power. Our work provides a decision support tool for investors to find profitable investment opportunities.

Model-agnostic meta-learners for estimating heterogeneous treatment effects over time

Estimating heterogeneous treatment effects (HTEs) over time is crucial in many disciplines such as personalized medicine. For example, electronic health records are commonly collected over several time periods and then used to personalize treatment decisions. Existing works for this task have mostly focused on model-based learners (i.e., learners that adapt specific machine-learning models). In contrast, model-agnostic learners -- so-called meta-learners -- are largely unexplored. In our paper, we propose several meta-learners that are model-agnostic and thus can be used in combination with arbitrary machine learning models (e.g., transformers) to estimate HTEs over time. Here, our focus is on learners that can be obtained via weighted pseudo-outcome regressions, which allows for efficient estimation by targeting the treatment effect directly. We then provide a comprehensive theoretical analysis that characterizes the different learners and that allows us to offer insights into when specific learners are preferable. Finally, we confirm our theoretical insights through numerical experiments. In sum, while meta-learners are already state-of-the-art for the static setting, we are the first to propose a comprehensive set of meta-learners for estimating HTEs in the time-varying setting.