Foundation Models for Causal Inference via Prior-Data Fitted Networks

Prior-data fitted networks (PFNs) have recently been proposed as a promising way to train tabular foundation models. PFNs are transformers that are pre-trained on synthetic data generated from a prespecified prior distribution and that enable Bayesian inference through in-context learning. In this paper, we introduce CausalFM, a comprehensive framework for training PFN-based foundation models in various causal inference settings. First, we formalize the construction of Bayesian priors for causal inference based on structural causal models (SCMs) in a principled way and derive necessary criteria for the validity of such priors. Building on this, we propose a novel family of prior distributions using causality-inspired Bayesian neural networks that enable CausalFM to perform Bayesian causal inference in various settings, including back-door, front-door, and instrumental variable adjustment. Finally, we instantiate CausalFM and explicitly train a foundation model for estimating conditional average treatment effects (CATEs) using back-door adjustment. We show that CausalFM performs competitively for CATE estimation using various synthetic and semi-synthetic benchmarks. In sum, our framework can be used as a general recipe to train foundation models for various causal inference settings. In contrast to the current state-of-the-art in causal inference, CausalFM offers a novel paradigm with the potential to fundamentally change how practitioners perform causal inference in medicine, economics, and other disciplines.

Treatment Effect Estimation for Optimal Decision-Making

Decision-making across various fields, such as medicine, heavily relies on conditional average treatment effects (CATEs). Practitioners commonly make decisions by checking whether the estimated CATE is positive, even though the decision-making performance of modern CATE estimators is poorly understood from a theoretical perspective. In this paper, we study optimal decision-making based on two-stage CATE estimators (e.g., DR-learner), which are considered state-of-the-art and widely used in practice. We prove that, while such estimators may be optimal for estimating CATE, they can be suboptimal when used for decision-making. Intuitively, this occurs because such estimators prioritize CATE accuracy in regions far away from the decision boundary, which is ultimately irrelevant to decision-making. As a remedy, we propose a novel two-stage learning objective that retargets the CATE to balance CATE estimation error and decision performance. We then propose a neural method that optimizes an adaptively-smoothed approximation of our learning objective. Finally, we confirm the effectiveness of our method both empirically and theoretically. In sum, our work is the first to show how two-stage CATE estimators can be adapted for optimal decision-making.

Orthogonal Survival Learners for Estimating Heterogeneous Treatment Effects from Time-to-Event Data

Estimating heterogeneous treatment effects (HTEs) is crucial for personalized decision-making. However, this task is challenging in survival analysis, which includes time-to-event data with censored outcomes (e.g., due to study dropout). In this paper, we propose a toolbox of novel orthogonal survival learners to estimate HTEs from time-to-event data under censoring. Our learners have three main advantages: (i) we show that learners from our toolbox are guaranteed to be orthogonal and thus come with favorable theoretical properties; (ii) our toolbox allows for incorporating a custom weighting function, which can lead to robustness against different types of low overlap, and (iii) our learners are model-agnostic (i.e., they can be combined with arbitrary machine learning models). We instantiate the learners from our toolbox using several weighting functions and, as a result, propose various neural orthogonal survival learners. Some of these coincide with existing survival learners (including survival versions of the DR- and R-learner), while others are novel and further robust w.r.t. low overlap regimes specific to the survival setting (i.e., survival overlap and censoring overlap). We then empirically verify the effectiveness of our learners for HTE estimation in different low-overlap regimes through numerical experiments. In sum, we provide practitioners with a large toolbox of learners that can be used for randomized and observational studies with censored time-to-event data.

Efficient and Sharp Off-Policy Learning under Unobserved Confounding

We develop a novel method for personalized off-policy learning in scenarios with unobserved confounding. Thereby, we address a key limitation of standard policy learning: standard policy learning assumes unconfoundedness, meaning that no unobserved factors influence both treatment assignment and outcomes. However, this assumption is often violated, because of which standard policy learning produces biased estimates and thus leads to policies that can be harmful. To address this limitation, we employ causal sensitivity analysis and derive a statistically efficient estimator for a sharp bound on the value function under unobserved confounding. Our estimator has three advantages: (1) Unlike existing works, our estimator avoids unstable minimax optimization based on inverse propensity weighted outcomes. (2) Our estimator is statistically efficient. (3) We prove that our estimator leads to the optimal confounding-robust policy. Finally, we extend our theory to the related task of policy improvement under unobserved confounding, i.e., when a baseline policy such as the standard of care is available. We show in experiments with synthetic and real-world data that our method outperforms simple plug-in approaches and existing baselines. Our method is highly relevant for decision-making where unobserved confounding can be problematic, such as in healthcare and public policy.

Orthogonal Representation Learning for Estimating Causal Quantities

Representation learning is widely used for estimating causal quantities (e.g., the conditional average treatment effect) from observational data. While existing representation learning methods have the benefit of allowing for end-to-end learning, they do not have favorable theoretical properties of Neyman-orthogonal learners, such as double robustness and quasi-oracle efficiency. Also, such representation learning methods often employ additional constraints, like balancing, which may even lead to inconsistent estimation. In this paper, we propose a novel class of Neyman-orthogonal learners for causal quantities defined at the representation level, which we call OR-learners. Our OR-learners have several practical advantages: they allow for consistent estimation of causal quantities based on any learned representation, while offering favorable theoretical properties including double robustness and quasi-oracle efficiency. In multiple experiments, we show that, under certain regularity conditions, our OR-learners improve existing representation learning methods and achieve state-of-the-art performance. To the best of our knowledge, our OR-learners are the first work to offer a unified framework of representation learning methods and Neyman-orthogonal learners for causal quantities estimation.

Constructing Confidence Intervals for Average Treatment Effects from Multiple Datasets

Constructing confidence intervals (CIs) for the average treatment effect (ATE) from patient records is crucial to assess the effectiveness and safety of drugs. However, patient records typically come from different hospitals, thus raising the question of how multiple observational datasets can be effectively combined for this purpose. In our paper, we propose a new method that estimates the ATE from multiple observational datasets and provides valid CIs. Our method makes little assumptions about the observational datasets and is thus widely applicable in medical practice. The key idea of our method is that we leverage prediction-powered inferences and thereby essentially `shrink' the CIs so that we offer more precise uncertainty quantification as compared to na\"ive approaches. We further prove the unbiasedness of our method and the validity of our CIs. We confirm our theoretical results through various numerical experiments. Finally, we provide an extension of our method for constructing CIs from combinations of experimental and observational datasets.

Causal machine learning for predicting treatment outcomes

Causal machine learning (ML) offers flexible, data-driven methods for predicting treatment outcomes including efficacy and toxicity, thereby supporting the assessment and safety of drugs. A key benefit of causal ML is that it allows for estimating individualized treatment effects, so that clinical decision-making can be personalized to individual patient profiles. Causal ML can be used in combination with both clinical trial data and real-world data, such as clinical registries and electronic health records, but caution is needed to avoid biased or incorrect predictions. In this Perspective, we discuss the benefits of causal ML (relative to traditional statistical or ML approaches) and outline the key components and steps. Finally, we provide recommendations for the reliable use of causal ML and effective translation into the clinic.

Learning Representations of Instruments for Partial Identification of Treatment Effects

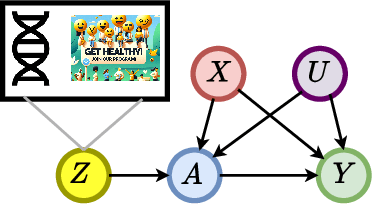
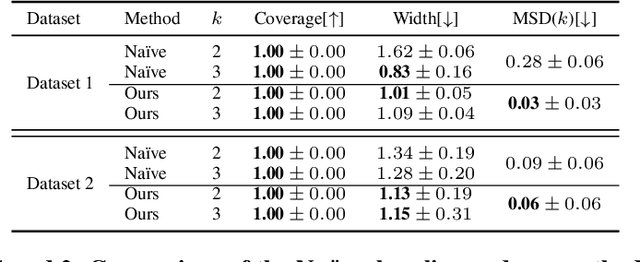
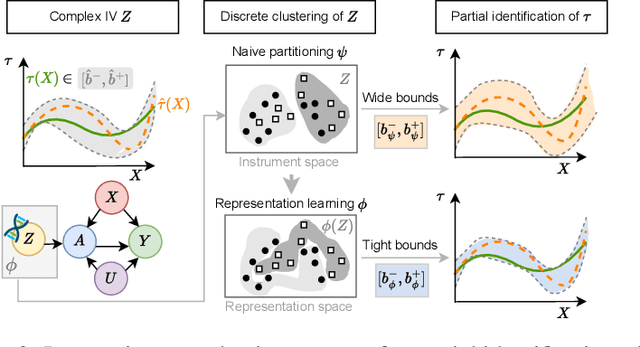
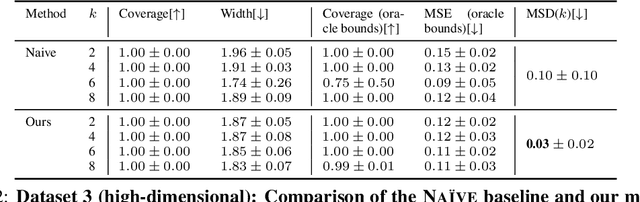
Reliable estimation of treatment effects from observational data is important in many disciplines such as medicine. However, estimation is challenging when unconfoundedness as a standard assumption in the causal inference literature is violated. In this work, we leverage arbitrary (potentially high-dimensional) instruments to estimate bounds on the conditional average treatment effect (CATE). Our contributions are three-fold: (1) We propose a novel approach for partial identification through a mapping of instruments to a discrete representation space so that we yield valid bounds on the CATE. This is crucial for reliable decision-making in real-world applications. (2) We derive a two-step procedure that learns tight bounds using a tailored neural partitioning of the latent instrument space. As a result, we avoid instability issues due to numerical approximations or adversarial training. Furthermore, our procedure aims to reduce the estimation variance in finite-sample settings to yield more reliable estimates. (3) We show theoretically that our procedure obtains valid bounds while reducing estimation variance. We further perform extensive experiments to demonstrate the effectiveness across various settings. Overall, our procedure offers a novel path for practitioners to make use of potentially high-dimensional instruments (e.g., as in Mendelian randomization).

Model-agnostic meta-learners for estimating heterogeneous treatment effects over time

Estimating heterogeneous treatment effects (HTEs) over time is crucial in many disciplines such as personalized medicine. For example, electronic health records are commonly collected over several time periods and then used to personalize treatment decisions. Existing works for this task have mostly focused on model-based learners (i.e., learners that adapt specific machine-learning models). In contrast, model-agnostic learners -- so-called meta-learners -- are largely unexplored. In our paper, we propose several meta-learners that are model-agnostic and thus can be used in combination with arbitrary machine learning models (e.g., transformers) to estimate HTEs over time. Here, our focus is on learners that can be obtained via weighted pseudo-outcome regressions, which allows for efficient estimation by targeting the treatment effect directly. We then provide a comprehensive theoretical analysis that characterizes the different learners and that allows us to offer insights into when specific learners are preferable. Finally, we confirm our theoretical insights through numerical experiments. In sum, while meta-learners are already state-of-the-art for the static setting, we are the first to propose a comprehensive set of meta-learners for estimating HTEs in the time-varying setting.

Conformal Prediction for Causal Effects of Continuous Treatments

Uncertainty quantification of causal effects is crucial for safety-critical applications such as personalized medicine. A powerful approach for this is conformal prediction, which has several practical benefits due to model-agnostic finite-sample guarantees. Yet, existing methods for conformal prediction of causal effects are limited to binary/discrete treatments and make highly restrictive assumptions such as known propensity scores. In this work, we provide a novel conformal prediction method for potential outcomes of continuous treatments. We account for the additional uncertainty introduced through propensity estimation so that our conformal prediction intervals are valid even if the propensity score is unknown. Our contributions are three-fold: (1) We derive finite-sample prediction intervals for potential outcomes of continuous treatments. (2) We provide an algorithm for calculating the derived intervals. (3) We demonstrate the effectiveness of the conformal prediction intervals in experiments on synthetic and real-world datasets. To the best of our knowledge, we are the first to propose conformal prediction for continuous treatments when the propensity score is unknown and must be estimated from data.