Efficient and Sharp Off-Policy Learning under Unobserved Confounding

We develop a novel method for personalized off-policy learning in scenarios with unobserved confounding. Thereby, we address a key limitation of standard policy learning: standard policy learning assumes unconfoundedness, meaning that no unobserved factors influence both treatment assignment and outcomes. However, this assumption is often violated, because of which standard policy learning produces biased estimates and thus leads to policies that can be harmful. To address this limitation, we employ causal sensitivity analysis and derive a statistically efficient estimator for a sharp bound on the value function under unobserved confounding. Our estimator has three advantages: (1) Unlike existing works, our estimator avoids unstable minimax optimization based on inverse propensity weighted outcomes. (2) Our estimator is statistically efficient. (3) We prove that our estimator leads to the optimal confounding-robust policy. Finally, we extend our theory to the related task of policy improvement under unobserved confounding, i.e., when a baseline policy such as the standard of care is available. We show in experiments with synthetic and real-world data that our method outperforms simple plug-in approaches and existing baselines. Our method is highly relevant for decision-making where unobserved confounding can be problematic, such as in healthcare and public policy.

Orthogonal Representation Learning for Estimating Causal Quantities

Representation learning is widely used for estimating causal quantities (e.g., the conditional average treatment effect) from observational data. While existing representation learning methods have the benefit of allowing for end-to-end learning, they do not have favorable theoretical properties of Neyman-orthogonal learners, such as double robustness and quasi-oracle efficiency. Also, such representation learning methods often employ additional constraints, like balancing, which may even lead to inconsistent estimation. In this paper, we propose a novel class of Neyman-orthogonal learners for causal quantities defined at the representation level, which we call OR-learners. Our OR-learners have several practical advantages: they allow for consistent estimation of causal quantities based on any learned representation, while offering favorable theoretical properties including double robustness and quasi-oracle efficiency. In multiple experiments, we show that, under certain regularity conditions, our OR-learners improve existing representation learning methods and achieve state-of-the-art performance. To the best of our knowledge, our OR-learners are the first work to offer a unified framework of representation learning methods and Neyman-orthogonal learners for causal quantities estimation.

Quantifying Aleatoric Uncertainty of the Treatment Effect: A Novel Orthogonal Learner

Estimating causal quantities from observational data is crucial for understanding the safety and effectiveness of medical treatments. However, to make reliable inferences, medical practitioners require not only estimating averaged causal quantities, such as the conditional average treatment effect, but also understanding the randomness of the treatment effect as a random variable. This randomness is referred to as aleatoric uncertainty and is necessary for understanding the probability of benefit from treatment or quantiles of the treatment effect. Yet, the aleatoric uncertainty of the treatment effect has received surprisingly little attention in the causal machine learning community. To fill this gap, we aim to quantify the aleatoric uncertainty of the treatment effect at the covariate-conditional level, namely, the conditional distribution of the treatment effect (CDTE). Unlike average causal quantities, the CDTE is not point identifiable without strong additional assumptions. As a remedy, we employ partial identification to obtain sharp bounds on the CDTE and thereby quantify the aleatoric uncertainty of the treatment effect. We then develop a novel, orthogonal learner for the bounds on the CDTE, which we call AU-learner. We further show that our AU-learner has several strengths in that it satisfies Neyman-orthogonality and is doubly robust. Finally, we propose a fully-parametric deep learning instantiation of our AU-learner.

Causal machine learning for predicting treatment outcomes

Causal machine learning (ML) offers flexible, data-driven methods for predicting treatment outcomes including efficacy and toxicity, thereby supporting the assessment and safety of drugs. A key benefit of causal ML is that it allows for estimating individualized treatment effects, so that clinical decision-making can be personalized to individual patient profiles. Causal ML can be used in combination with both clinical trial data and real-world data, such as clinical registries and electronic health records, but caution is needed to avoid biased or incorrect predictions. In this Perspective, we discuss the benefits of causal ML (relative to traditional statistical or ML approaches) and outline the key components and steps. Finally, we provide recommendations for the reliable use of causal ML and effective translation into the clinic.

DiffPO: A causal diffusion model for learning distributions of potential outcomes

Predicting potential outcomes of interventions from observational data is crucial for decision-making in medicine, but the task is challenging due to the fundamental problem of causal inference. Existing methods are largely limited to point estimates of potential outcomes with no uncertain quantification; thus, the full information about the distributions of potential outcomes is typically ignored. In this paper, we propose a novel causal diffusion model called DiffPO, which is carefully designed for reliable inferences in medicine by learning the distribution of potential outcomes. In our DiffPO, we leverage a tailored conditional denoising diffusion model to learn complex distributions, where we address the selection bias through a novel orthogonal diffusion loss. Another strength of our DiffPO method is that it is highly flexible (e.g., it can also be used to estimate different causal quantities such as CATE). Across a wide range of experiments, we show that our method achieves state-of-the-art performance.

Conformal Prediction for Causal Effects of Continuous Treatments

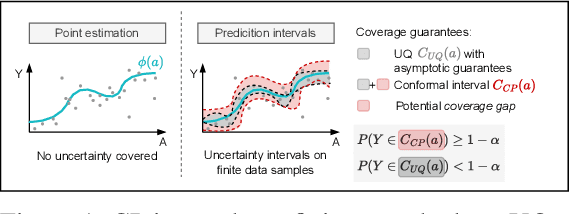
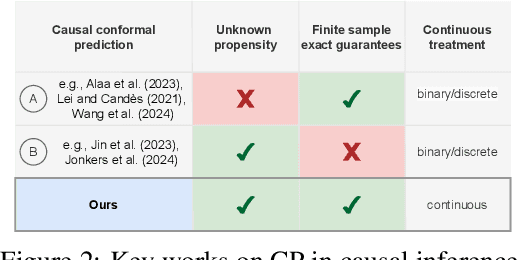
Uncertainty quantification of causal effects is crucial for safety-critical applications such as personalized medicine. A powerful approach for this is conformal prediction, which has several practical benefits due to model-agnostic finite-sample guarantees. Yet, existing methods for conformal prediction of causal effects are limited to binary/discrete treatments and make highly restrictive assumptions such as known propensity scores. In this work, we provide a novel conformal prediction method for potential outcomes of continuous treatments. We account for the additional uncertainty introduced through propensity estimation so that our conformal prediction intervals are valid even if the propensity score is unknown. Our contributions are three-fold: (1) We derive finite-sample prediction intervals for potential outcomes of continuous treatments. (2) We provide an algorithm for calculating the derived intervals. (3) We demonstrate the effectiveness of the conformal prediction intervals in experiments on synthetic and real-world datasets. To the best of our knowledge, we are the first to propose conformal prediction for continuous treatments when the propensity score is unknown and must be estimated from data.

G-Transformer for Conditional Average Potential Outcome Estimation over Time

Estimating potential outcomes for treatments over time based on observational data is important for personalized decision-making in medicine. Yet, existing neural methods for this task suffer from either (a) bias or (b) large variance. In order to address both limitations, we introduce the G-transformer (GT). Our GT is a novel, neural end-to-end model designed for unbiased, low-variance estimation of conditional average potential outcomes (CAPOs) over time. Specifically, our GT is the first neural model to perform regression-based iterative G-computation for CAPOs in the time-varying setting. We evaluate the effectiveness of our GT across various experiments. In sum, this work represents a significant step towards personalized decision-making from electronic health records.

A Neural Framework for Generalized Causal Sensitivity Analysis

Unobserved confounding is common in many applications, making causal inference from observational data challenging. As a remedy, causal sensitivity analysis is an important tool to draw causal conclusions under unobserved confounding with mathematical guarantees. In this paper, we propose NeuralCSA, a neural framework for generalized causal sensitivity analysis. Unlike previous work, our framework is compatible with (i) a large class of sensitivity models, including the marginal sensitivity model, f-sensitivity models, and Rosenbaum's sensitivity model; (ii) different treatment types (i.e., binary and continuous); and (iii) different causal queries, including (conditional) average treatment effects and simultaneous effects on multiple outcomes. The generality of \frameworkname is achieved by learning a latent distribution shift that corresponds to a treatment intervention using two conditional normalizing flows. We provide theoretical guarantees that NeuralCSA is able to infer valid bounds on the causal query of interest and also demonstrate this empirically using both simulated and real-world data.

Bounds on Representation-Induced Confounding Bias for Treatment Effect Estimation

State-of-the-art methods for conditional average treatment effect (CATE) estimation make widespread use of representation learning. Here, the idea is to reduce the variance of the low-sample CATE estimation by a (potentially constrained) low-dimensional representation. However, low-dimensional representations can lose information about the observed confounders and thus lead to bias, because of which the validity of representation learning for CATE estimation is typically violated. In this paper, we propose a new, representation-agnostic framework for estimating bounds on the representation-induced confounding bias that comes from dimensionality reduction (or other constraints on the representations) in CATE estimation. First, we establish theoretically under which conditions CATEs are non-identifiable given low-dimensional (constrained) representations. Second, as our remedy, we propose to perform partial identification of CATEs or, equivalently, aim at estimating of lower and upper bounds of the representation-induced confounding bias. We demonstrate the effectiveness of our bounds in a series of experiments. In sum, our framework is of direct relevance in practice where the validity of CATE estimation is of importance.

Counterfactual Fairness for Predictions using Generative Adversarial Networks

Fairness in predictions is of direct importance in practice due to legal, ethical, and societal reasons. It is often achieved through counterfactual fairness, which ensures that the prediction for an individual is the same as that in a counterfactual world under a different sensitive attribute. However, achieving counterfactual fairness is challenging as counterfactuals are unobservable. In this paper, we develop a novel deep neural network called Generative Counterfactual Fairness Network (GCFN) for making predictions under counterfactual fairness. Specifically, we leverage a tailored generative adversarial network to directly learn the counterfactual distribution of the descendants of the sensitive attribute, which we then use to enforce fair predictions through a novel counterfactual mediator regularization. If the counterfactual distribution is learned sufficiently well, our method is mathematically guaranteed to ensure the notion of counterfactual fairness. Thereby, our GCFN addresses key shortcomings of existing baselines that are based on inferring latent variables, yet which (a) are potentially correlated with the sensitive attributes and thus lead to bias, and (b) have weak capability in constructing latent representations and thus low prediction performance. Across various experiments, our method achieves state-of-the-art performance. Using a real-world case study from recidivism prediction, we further demonstrate that our method makes meaningful predictions in practice.