Constructing Confidence Intervals for Average Treatment Effects from Multiple Datasets

Constructing confidence intervals (CIs) for the average treatment effect (ATE) from patient records is crucial to assess the effectiveness and safety of drugs. However, patient records typically come from different hospitals, thus raising the question of how multiple observational datasets can be effectively combined for this purpose. In our paper, we propose a new method that estimates the ATE from multiple observational datasets and provides valid CIs. Our method makes little assumptions about the observational datasets and is thus widely applicable in medical practice. The key idea of our method is that we leverage prediction-powered inferences and thereby essentially `shrink' the CIs so that we offer more precise uncertainty quantification as compared to na\"ive approaches. We further prove the unbiasedness of our method and the validity of our CIs. We confirm our theoretical results through various numerical experiments. Finally, we provide an extension of our method for constructing CIs from combinations of experimental and observational datasets.

Causal machine learning for predicting treatment outcomes

Causal machine learning (ML) offers flexible, data-driven methods for predicting treatment outcomes including efficacy and toxicity, thereby supporting the assessment and safety of drugs. A key benefit of causal ML is that it allows for estimating individualized treatment effects, so that clinical decision-making can be personalized to individual patient profiles. Causal ML can be used in combination with both clinical trial data and real-world data, such as clinical registries and electronic health records, but caution is needed to avoid biased or incorrect predictions. In this Perspective, we discuss the benefits of causal ML (relative to traditional statistical or ML approaches) and outline the key components and steps. Finally, we provide recommendations for the reliable use of causal ML and effective translation into the clinic.

Learning Representations of Instruments for Partial Identification of Treatment Effects

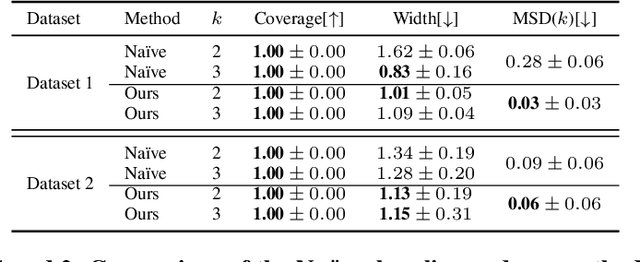
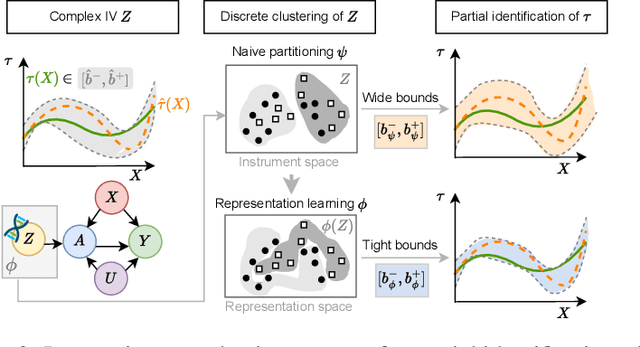
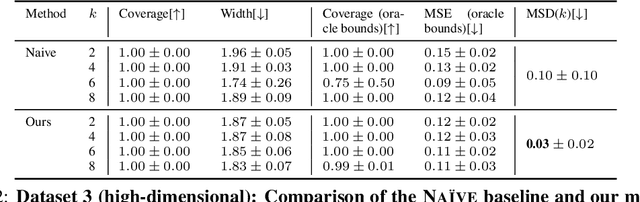
Reliable estimation of treatment effects from observational data is important in many disciplines such as medicine. However, estimation is challenging when unconfoundedness as a standard assumption in the causal inference literature is violated. In this work, we leverage arbitrary (potentially high-dimensional) instruments to estimate bounds on the conditional average treatment effect (CATE). Our contributions are three-fold: (1) We propose a novel approach for partial identification through a mapping of instruments to a discrete representation space so that we yield valid bounds on the CATE. This is crucial for reliable decision-making in real-world applications. (2) We derive a two-step procedure that learns tight bounds using a tailored neural partitioning of the latent instrument space. As a result, we avoid instability issues due to numerical approximations or adversarial training. Furthermore, our procedure aims to reduce the estimation variance in finite-sample settings to yield more reliable estimates. (3) We show theoretically that our procedure obtains valid bounds while reducing estimation variance. We further perform extensive experiments to demonstrate the effectiveness across various settings. Overall, our procedure offers a novel path for practitioners to make use of potentially high-dimensional instruments (e.g., as in Mendelian randomization).

Stabilized Neural Prediction of Potential Outcomes in Continuous Time

Patient trajectories from electronic health records are widely used to predict potential outcomes of treatments over time, which then allows to personalize care. Yet, existing neural methods for this purpose have a key limitation: while some adjust for time-varying confounding, these methods assume that the time series are recorded in discrete time. In other words, they are constrained to settings where measurements and treatments are conducted at fixed time steps, even though this is unrealistic in medical practice. In this work, we aim to predict potential outcomes in continuous time. The latter is of direct practical relevance because it allows for modeling patient trajectories where measurements and treatments take place at arbitrary, irregular timestamps. We thus propose a new method called stabilized continuous time inverse propensity network (SCIP-Net). For this, we further derive stabilized inverse propensity weights for robust prediction of the potential outcomes. To the best of our knowledge, our SCIP-Net is the first neural method that performs proper adjustments for time-varying confounding in continuous time.

Model-agnostic meta-learners for estimating heterogeneous treatment effects over time

Estimating heterogeneous treatment effects (HTEs) over time is crucial in many disciplines such as personalized medicine. For example, electronic health records are commonly collected over several time periods and then used to personalize treatment decisions. Existing works for this task have mostly focused on model-based learners (i.e., learners that adapt specific machine-learning models). In contrast, model-agnostic learners -- so-called meta-learners -- are largely unexplored. In our paper, we propose several meta-learners that are model-agnostic and thus can be used in combination with arbitrary machine learning models (e.g., transformers) to estimate HTEs over time. Here, our focus is on learners that can be obtained via weighted pseudo-outcome regressions, which allows for efficient estimation by targeting the treatment effect directly. We then provide a comprehensive theoretical analysis that characterizes the different learners and that allows us to offer insights into when specific learners are preferable. Finally, we confirm our theoretical insights through numerical experiments. In sum, while meta-learners are already state-of-the-art for the static setting, we are the first to propose a comprehensive set of meta-learners for estimating HTEs in the time-varying setting.

G-Transformer for Conditional Average Potential Outcome Estimation over Time

Estimating potential outcomes for treatments over time based on observational data is important for personalized decision-making in medicine. Yet, existing neural methods for this task suffer from either (a) bias or (b) large variance. In order to address both limitations, we introduce the G-transformer (GT). Our GT is a novel, neural end-to-end model designed for unbiased, low-variance estimation of conditional average potential outcomes (CAPOs) over time. Specifically, our GT is the first neural model to perform regression-based iterative G-computation for CAPOs in the time-varying setting. We evaluate the effectiveness of our GT across various experiments. In sum, this work represents a significant step towards personalized decision-making from electronic health records.

Bayesian Neural Controlled Differential Equations for Treatment Effect Estimation

Treatment effect estimation in continuous time is crucial for personalized medicine. However, existing methods for this task are limited to point estimates of the potential outcomes, whereas uncertainty estimates have been ignored. Needless to say, uncertainty quantification is crucial for reliable decision-making in medical applications. To fill this gap, we propose a novel Bayesian neural controlled differential equation (BNCDE) for treatment effect estimation in continuous time. In our BNCDE, the time dimension is modeled through a coupled system of neural controlled differential equations and neural stochastic differential equations, where the neural stochastic differential equations allow for tractable variational Bayesian inference. Thereby, for an assigned sequence of treatments, our BNCDE provides meaningful posterior predictive distributions of the potential outcomes. To the best of our knowledge, ours is the first tailored neural method to provide uncertainty estimates of treatment effects in continuous time. As such, our method is of direct practical value for promoting reliable decision-making in medicine.