Your Assumed DAG is Wrong and Here's How To Deal With It

Assuming a directed acyclic graph (DAG) that represents prior knowledge of causal relationships between variables is a common starting point for cause-effect estimation. Existing literature typically invokes hypothetical domain expert knowledge or causal discovery algorithms to justify this assumption. In practice, neither may propose a single DAG with high confidence. Domain experts are hesitant to rule out dependencies with certainty or have ongoing disputes about relationships; causal discovery often relies on untestable assumptions itself or only provides an equivalence class of DAGs and is commonly sensitive to hyperparameter and threshold choices. We propose an efficient, gradient-based optimization method that provides bounds for causal queries over a collection of causal graphs -- compatible with imperfect prior knowledge -- that may still be too large for exhaustive enumeration. Our bounds achieve good coverage and sharpness for causal queries such as average treatment effects in linear and non-linear synthetic settings as well as on real-world data. Our approach aims at providing an easy-to-use and widely applicable rebuttal to the valid critique of `What if your assumed DAG is wrong?'.

Auditing a Dutch Public Sector Risk Profiling Algorithm Using an Unsupervised Bias Detection Tool

Algorithms are increasingly used to automate or aid human decisions, yet recent research shows that these algorithms may exhibit bias across legally protected demographic groups. However, data on these groups may be unavailable to organizations or external auditors due to privacy legislation. This paper studies bias detection using an unsupervised clustering tool when data on demographic groups are unavailable. We collaborate with the Dutch Executive Agency for Education to audit an algorithm that was used to assign risk scores to college students at the national level in the Netherlands between 2012-2023. Our audit covers more than 250,000 students from the whole country. The unsupervised clustering tool highlights known disparities between students with a non-European migration background and Dutch origin. Our contributions are three-fold: (1) we assess bias in a real-world, large-scale and high-stakes decision-making process by a governmental organization; (2) we use simulation studies to highlight potential pitfalls of using the unsupervised clustering tool to detect true bias when demographic group data are unavailable and provide recommendations for valid inferences; (3) we provide the unsupervised clustering tool in an open-source library. Our work serves as a starting point for a deliberative assessment by human experts to evaluate potential discrimination in algorithmic-supported decision-making processes.

Stochastic Causal Programming for Bounding Treatment Effects

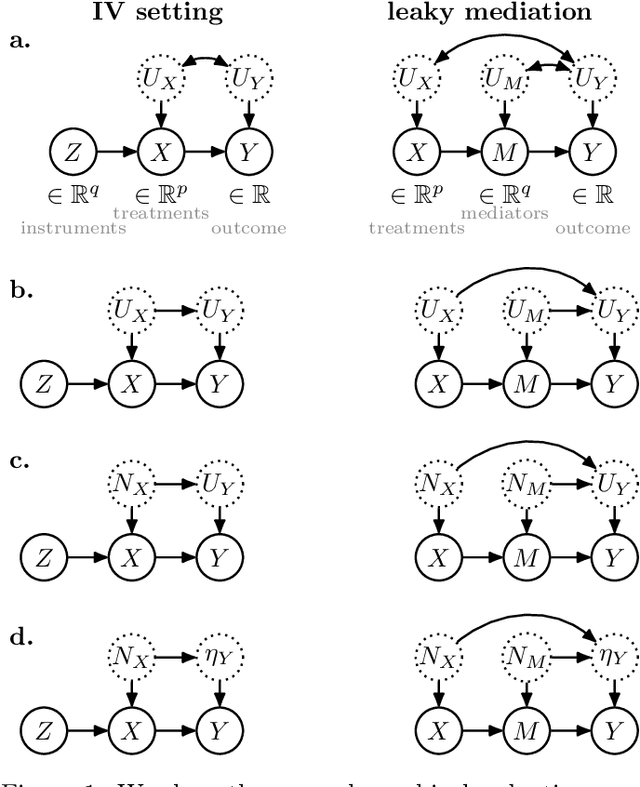
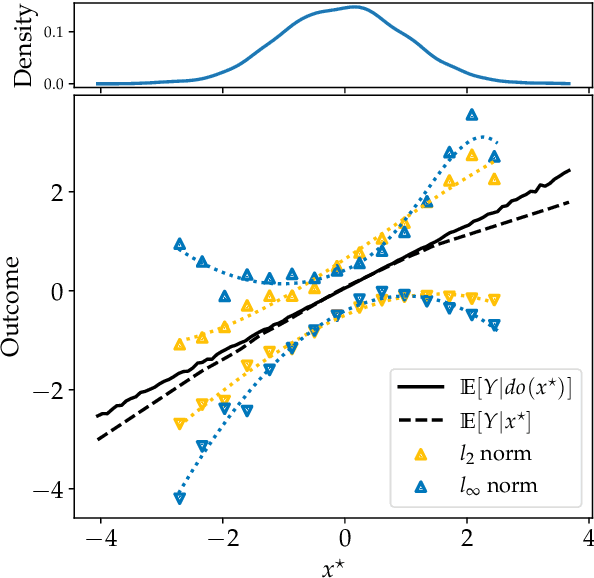
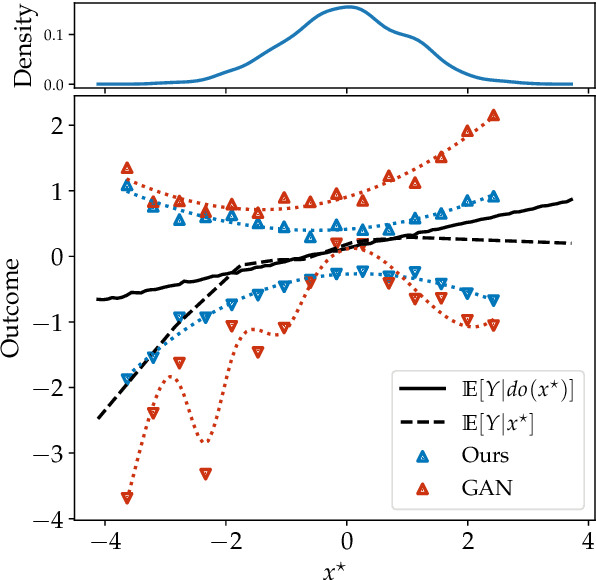
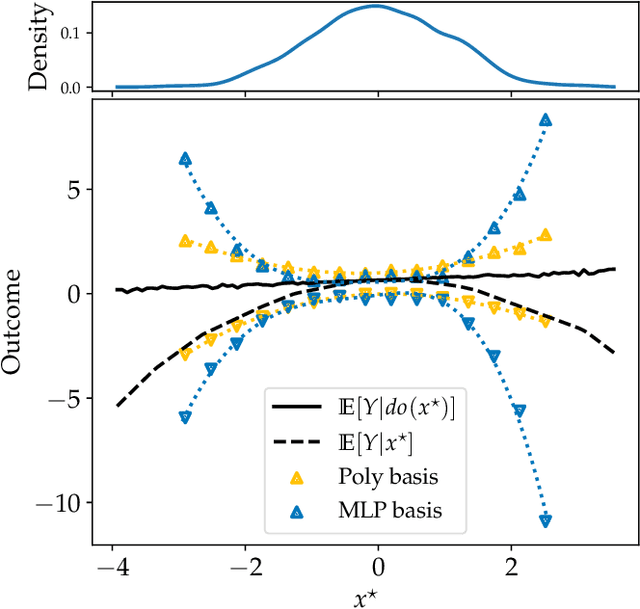
Causal effect estimation is important for numerous tasks in the natural and social sciences. However, identifying effects is impossible from observational data without making strong, often untestable assumptions. We consider algorithms for the partial identification problem, bounding treatment effects from multivariate, continuous treatments over multiple possible causal models when unmeasured confounding makes identification impossible. We consider a framework where observable evidence is matched to the implications of constraints encoded in a causal model by norm-based criteria. This generalizes classical approaches based purely on generative models. Casting causal effects as objective functions in a constrained optimization problem, we combine flexible learning algorithms with Monte Carlo methods to implement a family of solutions under the name of stochastic causal programming. In particular, we present ways by which such constrained optimization problems can be parameterized without likelihood functions for the causal or the observed data model, reducing the computational and statistical complexity of the task.

Addressing Fairness in Classification with a Model-Agnostic Multi-Objective Algorithm

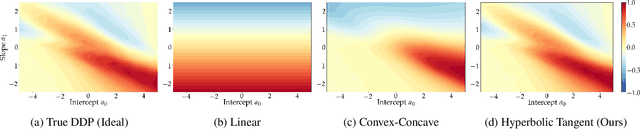
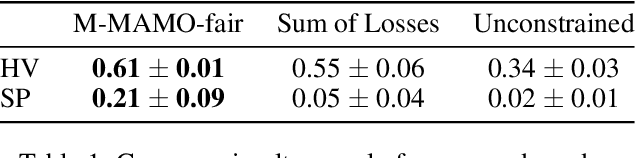
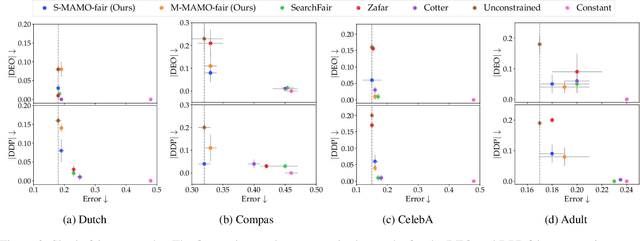
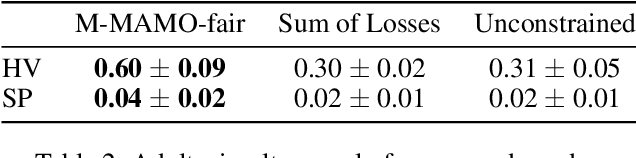
The goal of fairness in classification is to learn a classifier that does not discriminate against groups of individuals based on sensitive attributes, such as race and gender. One approach to designing fair algorithms is to use relaxations of fairness notions as regularization terms or in a constrained optimization problem. We observe that the hyperbolic tangent function can approximate the indicator function. We leverage this property to define a differentiable relaxation that approximates fairness notions provably better than existing relaxations. In addition, we propose a model-agnostic multi-objective architecture that can simultaneously optimize for multiple fairness notions and multiple sensitive attributes and supports all statistical parity-based notions of fairness. We use our relaxation with the multi-objective architecture to learn fair classifiers. Experiments on public datasets show that our method suffers a significantly lower loss of accuracy than current debiasing algorithms relative to the unconstrained model.