Long-run Behaviour of Multi-fidelity Bayesian Optimisation

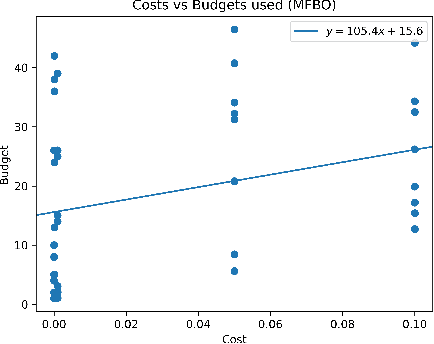
Multi-fidelity Bayesian Optimisation (MFBO) has been shown to generally converge faster than single-fidelity Bayesian Optimisation (SFBO) (Poloczek et al. (2017)). Inspired by recent benchmark papers, we are investigating the long-run behaviour of MFBO, based on observations in the literature that it might under-perform in certain scenarios (Mikkola et al. (2023), Eggensperger et al. (2021)). An under-performance of MBFO in the long-run could significantly undermine its application to many research tasks, especially when we are not able to identify when the under-performance begins. We create a simple benchmark study, showcase empirical results and discuss scenarios and possible reasons of under-performance.

Search Strategies for Self-driving Laboratories with Pending Experiments

Self-driving laboratories (SDLs) consist of multiple stations that perform material synthesis and characterisation tasks. To minimize station downtime and maximize experimental throughput, it is practical to run experiments in asynchronous parallel, in which multiple experiments are being performed at once in different stages. Asynchronous parallelization of experiments, however, introduces delayed feedback (i.e. "pending experiments"), which is known to reduce Bayesian optimiser performance. Here, we build a simulator for a multi-stage SDL and compare optimisation strategies for dealing with delayed feedback and asynchronous parallelized operation. Using data from a real SDL, we build a ground truth Bayesian optimisation simulator from 177 previously run experiments for maximizing the conductivity of functional coatings. We then compare search strategies such as expected improvement, noisy expected improvement, 4-mode exploration and random sampling. We evaluate their performance in terms of amount of delay and problem dimensionality. Our simulation results showcase the trade-off between the asynchronous parallel operation and delayed feedback.

Multi-fidelity Bayesian Optimisation of Syngas Fermentation Simulators

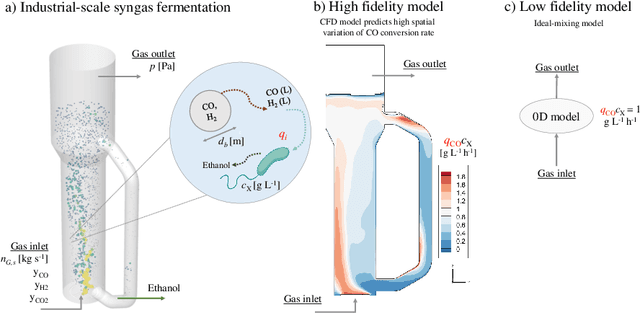
A Bayesian optimization approach for maximizing the gas conversion rate in an industrial-scale bioreactor for syngas fermentation is presented. We have access to a high-fidelity, computational fluid dynamic (CFD) reactor model and a low-fidelity ideal-mixing-based reactor model. The goal is to maximize the gas conversion rate, with respect to the input variables (e.g., pressure, biomass concentration, gas flow rate). Due to the high cost of the CFD reactor model, a multi-fidelity Bayesian optimization algorithm is adopted to solve the optimization problem using both high and low fidelities. We first describe the problem in the context of syngas fermentation followed by our approach to solving simulator optimization using multiple fidelities. We discuss concerns regarding significant differences in fidelity cost and their impact on fidelity sampling and conclude with a discussion on the integration of real-world fermentation data.

Intervention Generalization: A View from Factor Graph Models

One of the goals of causal inference is to generalize from past experiments and observational data to novel conditions. While it is in principle possible to eventually learn a mapping from a novel experimental condition to an outcome of interest, provided a sufficient variety of experiments is available in the training data, coping with a large combinatorial space of possible interventions is hard. Under a typical sparse experimental design, this mapping is ill-posed without relying on heavy regularization or prior distributions. Such assumptions may or may not be reliable, and can be hard to defend or test. In this paper, we take a close look at how to warrant a leap from past experiments to novel conditions based on minimal assumptions about the factorization of the distribution of the manipulated system, communicated in the well-understood language of factor graph models. A postulated $\textit{interventional factor model}$ (IFM) may not always be informative, but it conveniently abstracts away a need for explicit unmeasured confounding and feedback mechanisms, leading to directly testable claims. We derive necessary and sufficient conditions for causal effect identifiability with IFMs using data from a collection of experimental settings, and implement practical algorithms for generalizing expected outcomes to novel conditions never observed in the data.

Non-parametric identifiability and sensitivity analysis of synthetic control models

Quantifying cause and effect relationships is an important problem in many domains. The gold standard solution is to conduct a randomised controlled trial. However, in many situations such trials cannot be performed. In the absence of such trials, many methods have been devised to quantify the causal impact of an intervention from observational data given certain assumptions. One widely used method are synthetic control models. While identifiability of the causal estimand in such models has been obtained from a range of assumptions, it is widely and implicitly assumed that the underlying assumptions are satisfied for all time periods both pre- and post-intervention. This is a strong assumption, as synthetic control models can only be learned in pre-intervention period. In this paper we address this challenge, and prove identifiability can be obtained without the need for this assumption, by showing it follows from the principle of invariant causal mechanisms. Moreover, for the first time, we formulate and study synthetic control models in Pearl's structural causal model framework. Importantly, we provide a general framework for sensitivity analysis of synthetic control causal inference to violations of the assumptions underlying non-parametric identifiability. We end by providing an empirical demonstration of our sensitivity analysis framework on simulated and real data in the widely-used linear synthetic control framework.

The Causal Marginal Polytope for Bounding Treatment Effects

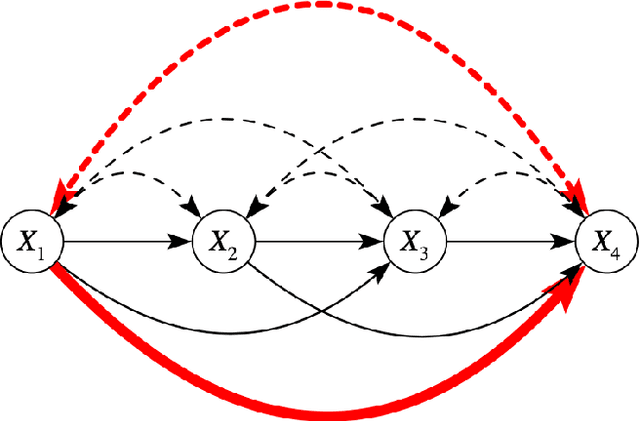
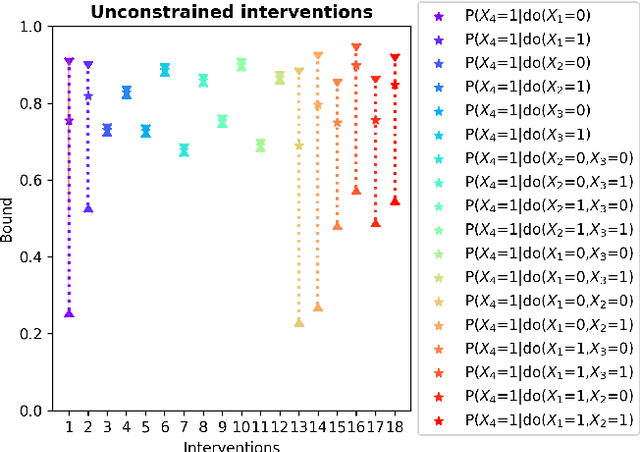
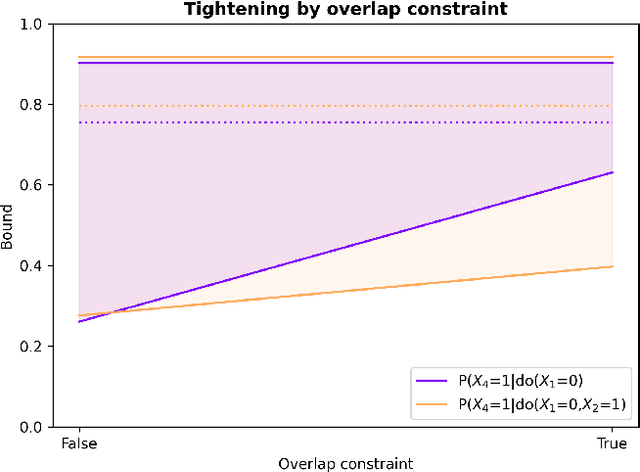
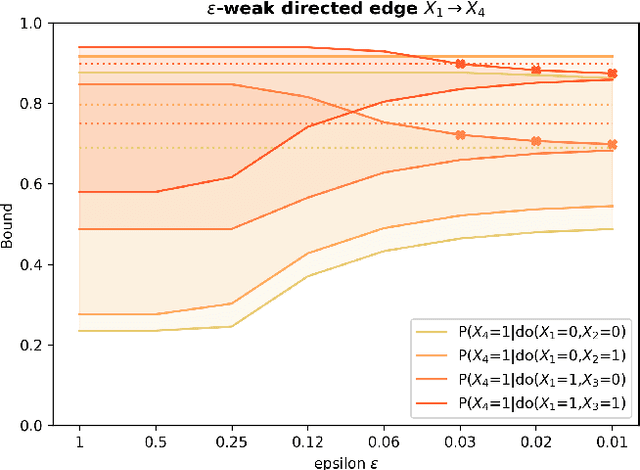
Due to unmeasured confounding, it is often not possible to identify causal effects from a postulated model. Nevertheless, we can ask for partial identification, which usually boils down to finding upper and lower bounds of a causal quantity of interest derived from all solutions compatible with the encoded structural assumptions. One appealing way to derive such bounds is by casting it in terms of a constrained optimization method that searches over all causal models compatible with evidence, as introduced in the classic work of Balke and Pearl (1994) for discrete data. Although by construction this guarantees tight bounds, it poses a formidable computational challenge. To cope with this issue, alternatives include algorithms that are not guaranteed to be tight, or by introducing restrictions on the class of models. In this paper, we introduce a novel alternative: inspired by ideas coming from belief propagation, we enforce compatibility between marginals of a causal model and data, without constructing a global causal model. We call this collection of locally consistent marginals the causal marginal polytope. As global independence constraints disappear when considering small dimensional tractable marginals, this also leads to a rethinking of how to elicit and express causal knowledge. We provide an explicit algorithm and implementation of this idea, and assess its practicality with numerical experiments.

Stochastic Causal Programming for Bounding Treatment Effects

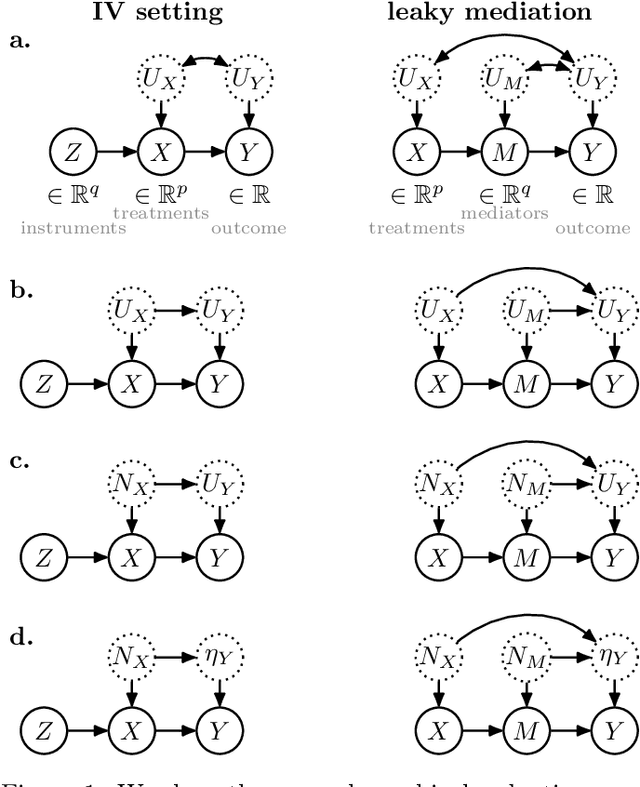
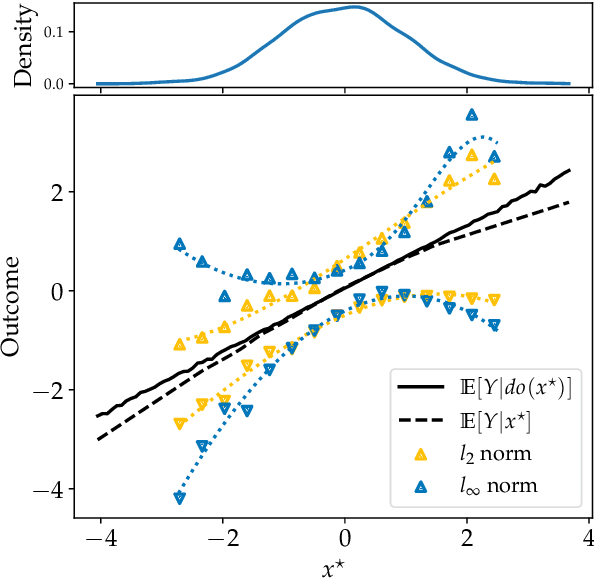
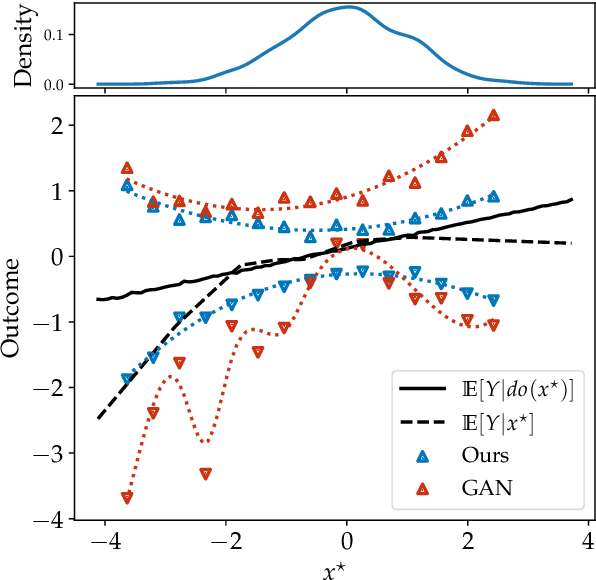
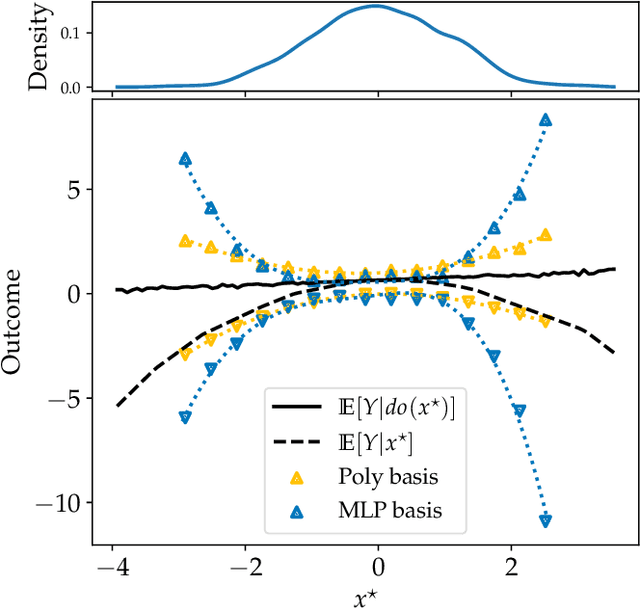
Causal effect estimation is important for numerous tasks in the natural and social sciences. However, identifying effects is impossible from observational data without making strong, often untestable assumptions. We consider algorithms for the partial identification problem, bounding treatment effects from multivariate, continuous treatments over multiple possible causal models when unmeasured confounding makes identification impossible. We consider a framework where observable evidence is matched to the implications of constraints encoded in a causal model by norm-based criteria. This generalizes classical approaches based purely on generative models. Casting causal effects as objective functions in a constrained optimization problem, we combine flexible learning algorithms with Monte Carlo methods to implement a family of solutions under the name of stochastic causal programming. In particular, we present ways by which such constrained optimization problems can be parameterized without likelihood functions for the causal or the observed data model, reducing the computational and statistical complexity of the task.

Algorithmic Recourse in Partially and Fully Confounded Settings Through Bounding Counterfactual Effects

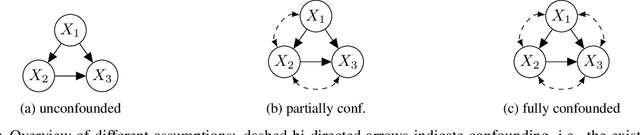
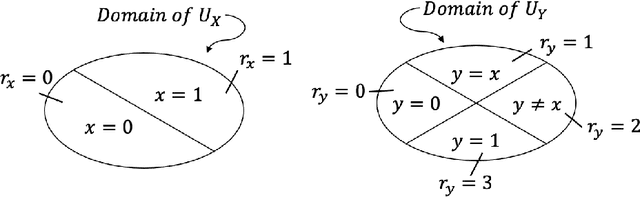
Algorithmic recourse aims to provide actionable recommendations to individuals to obtain a more favourable outcome from an automated decision-making system. As it involves reasoning about interventions performed in the physical world, recourse is fundamentally a causal problem. Existing methods compute the effect of recourse actions using a causal model learnt from data under the assumption of no hidden confounding and modelling assumptions such as additive noise. Building on the seminal work of Balke and Pearl (1994), we propose an alternative approach for discrete random variables which relaxes these assumptions and allows for unobserved confounding and arbitrary structural equations. The proposed approach only requires specification of the causal graph and confounding structure and bounds the expected counterfactual effect of recourse actions. If the lower bound is above a certain threshold, i.e., on the other side of the decision boundary, recourse is guaranteed in expectation.