Nikita Agarwal
Algorithmic Recourse in Partially and Fully Confounded Settings Through Bounding Counterfactual Effects
Jun 22, 2021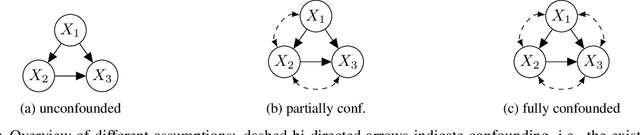
Abstract:Algorithmic recourse aims to provide actionable recommendations to individuals to obtain a more favourable outcome from an automated decision-making system. As it involves reasoning about interventions performed in the physical world, recourse is fundamentally a causal problem. Existing methods compute the effect of recourse actions using a causal model learnt from data under the assumption of no hidden confounding and modelling assumptions such as additive noise. Building on the seminal work of Balke and Pearl (1994), we propose an alternative approach for discrete random variables which relaxes these assumptions and allows for unobserved confounding and arbitrary structural equations. The proposed approach only requires specification of the causal graph and confounding structure and bounds the expected counterfactual effect of recourse actions. If the lower bound is above a certain threshold, i.e., on the other side of the decision boundary, recourse is guaranteed in expectation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge