Interaction Asymmetry: A General Principle for Learning Composable Abstractions

Learning disentangled representations of concepts and re-composing them in unseen ways is crucial for generalizing to out-of-domain situations. However, the underlying properties of concepts that enable such disentanglement and compositional generalization remain poorly understood. In this work, we propose the principle of interaction asymmetry which states: "Parts of the same concept have more complex interactions than parts of different concepts". We formalize this via block diagonality conditions on the $(n+1)$th order derivatives of the generator mapping concepts to observed data, where different orders of "complexity" correspond to different $n$. Using this formalism, we prove that interaction asymmetry enables both disentanglement and compositional generalization. Our results unify recent theoretical results for learning concepts of objects, which we show are recovered as special cases with $n\!=\!0$ or $1$. We provide results for up to $n\!=\!2$, thus extending these prior works to more flexible generator functions, and conjecture that the same proof strategies generalize to larger $n$. Practically, our theory suggests that, to disentangle concepts, an autoencoder should penalize its latent capacity and the interactions between concepts during decoding. We propose an implementation of these criteria using a flexible Transformer-based VAE, with a novel regularizer on the attention weights of the decoder. On synthetic image datasets consisting of objects, we provide evidence that this model can achieve comparable object disentanglement to existing models that use more explicit object-centric priors.

Identifiable Causal Representation Learning: Unsupervised, Multi-View, and Multi-Environment

Causal models provide rich descriptions of complex systems as sets of mechanisms by which each variable is influenced by its direct causes. They support reasoning about manipulating parts of the system and thus hold promise for addressing some of the open challenges of artificial intelligence (AI), such as planning, transferring knowledge in changing environments, or robustness to distribution shifts. However, a key obstacle to more widespread use of causal models in AI is the requirement that the relevant variables be specified a priori, which is typically not the case for the high-dimensional, unstructured data processed by modern AI systems. At the same time, machine learning (ML) has proven quite successful at automatically extracting useful and compact representations of such complex data. Causal representation learning (CRL) aims to combine the core strengths of ML and causality by learning representations in the form of latent variables endowed with causal model semantics. In this thesis, we study and present new results for different CRL settings. A central theme is the question of identifiability: Given infinite data, when are representations satisfying the same learning objective guaranteed to be equivalent? This is an important prerequisite for CRL, as it formally characterises if and when a learning task is, at least in principle, feasible. Since learning causal models, even without a representation learning component, is notoriously difficult, we require additional assumptions on the model class or rich data beyond the classical i.i.d. setting. By partially characterising identifiability for different settings, this thesis investigates what is possible for CRL without direct supervision, and thus contributes to its theoretical foundations. Ideally, the developed insights can help inform data collection practices or inspire the design of new practical estimation methods.

A Sparsity Principle for Partially Observable Causal Representation Learning

Causal representation learning aims at identifying high-level causal variables from perceptual data. Most methods assume that all latent causal variables are captured in the high-dimensional observations. We instead consider a partially observed setting, in which each measurement only provides information about a subset of the underlying causal state. Prior work has studied this setting with multiple domains or views, each depending on a fixed subset of latents. Here, we focus on learning from unpaired observations from a dataset with an instance-dependent partial observability pattern. Our main contribution is to establish two identifiability results for this setting: one for linear mixing functions without parametric assumptions on the underlying causal model, and one for piecewise linear mixing functions with Gaussian latent causal variables. Based on these insights, we propose two methods for estimating the underlying causal variables by enforcing sparsity in the inferred representation. Experiments on different simulated datasets and established benchmarks highlight the effectiveness of our approach in recovering the ground-truth latents.

Independent Mechanism Analysis and the Manifold Hypothesis

Independent Mechanism Analysis (IMA) seeks to address non-identifiability in nonlinear Independent Component Analysis (ICA) by assuming that the Jacobian of the mixing function has orthogonal columns. As typical in ICA, previous work focused on the case with an equal number of latent components and observed mixtures. Here, we extend IMA to settings with a larger number of mixtures that reside on a manifold embedded in a higher-dimensional than the latent space -- in line with the manifold hypothesis in representation learning. For this setting, we show that IMA still circumvents several non-identifiability issues, suggesting that it can also be a beneficial principle for higher-dimensional observations when the manifold hypothesis holds. Further, we prove that the IMA principle is approximately satisfied with high probability (increasing with the number of observed mixtures) when the directions along which the latent components influence the observations are chosen independently at random. This provides a new and rigorous statistical interpretation of IMA.

Self-Supervised Disentanglement by Leveraging Structure in Data Augmentations

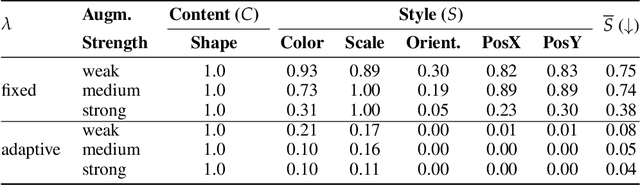
Self-supervised representation learning often uses data augmentations to induce some invariance to "style" attributes of the data. However, with downstream tasks generally unknown at training time, it is difficult to deduce a priori which attributes of the data are indeed "style" and can be safely discarded. To address this, we introduce a more principled approach that seeks to disentangle style features rather than discard them. The key idea is to add multiple style embedding spaces where: (i) each is invariant to all-but-one augmentation; and (ii) joint entropy is maximized. We formalize our structured data-augmentation procedure from a causal latent-variable-model perspective, and prove identifiability of both content and (multiple blocks of) style variables. We empirically demonstrate the benefits of our approach on synthetic datasets and then present promising but limited results on ImageNet.

Multi-View Causal Representation Learning with Partial Observability

We present a unified framework for studying the identifiability of representations learned from simultaneously observed views, such as different data modalities. We allow a partially observed setting in which each view constitutes a nonlinear mixture of a subset of underlying latent variables, which can be causally related. We prove that the information shared across all subsets of any number of views can be learned up to a smooth bijection using contrastive learning and a single encoder per view. We also provide graphical criteria indicating which latent variables can be identified through a simple set of rules, which we refer to as identifiability algebra. Our general framework and theoretical results unify and extend several previous works on multi-view nonlinear ICA, disentanglement, and causal representation learning. We experimentally validate our claims on numerical, image, and multi-modal data sets. Further, we demonstrate that the performance of prior methods is recovered in different special cases of our setup. Overall, we find that access to multiple partial views enables us to identify a more fine-grained representation, under the generally milder assumption of partial observability.

Deep Backtracking Counterfactuals for Causally Compliant Explanations

Counterfactuals can offer valuable insights by answering what would have been observed under altered circumstances, conditional on a factual observation. Whereas the classical interventional interpretation of counterfactuals has been studied extensively, backtracking constitutes a less studied alternative the backtracking principle has emerged as an alternative philosophy where all causal laws are kept intact. In the present work, we introduce a practical method for computing backtracking counterfactuals in structural causal models that consist of deep generative components. To this end, we impose conditions on the structural assignments that enable the generation of counterfactuals by solving a tractable constrained optimization problem in the structured latent space of a causal model. Our formulation also facilitates a comparison with methods in the field of counterfactual explanations. Compared to these, our method represents a versatile, modular and causally compliant alternative. We demonstrate these properties experimentally on a modified version of MNIST and CelebA.

Spuriosity Didn't Kill the Classifier: Using Invariant Predictions to Harness Spurious Features

To avoid failures on out-of-distribution data, recent works have sought to extract features that have a stable or invariant relationship with the label across domains, discarding the "spurious" or unstable features whose relationship with the label changes across domains. However, unstable features often carry complementary information about the label that could boost performance if used correctly in the test domain. Our main contribution is to show that it is possible to learn how to use these unstable features in the test domain without labels. In particular, we prove that pseudo-labels based on stable features provide sufficient guidance for doing so, provided that stable and unstable features are conditionally independent given the label. Based on this theoretical insight, we propose Stable Feature Boosting (SFB), an algorithm for: (i) learning a predictor that separates stable and conditionally-independent unstable features; and (ii) using the stable-feature predictions to adapt the unstable-feature predictions in the test domain. Theoretically, we prove that SFB can learn an asymptotically-optimal predictor without test-domain labels. Empirically, we demonstrate the effectiveness of SFB on real and synthetic data.

Causal Effect Estimation from Observational and Interventional Data Through Matrix Weighted Linear Estimators

We study causal effect estimation from a mixture of observational and interventional data in a confounded linear regression model with multivariate treatments. We show that the statistical efficiency in terms of expected squared error can be improved by combining estimators arising from both the observational and interventional setting. To this end, we derive methods based on matrix weighted linear estimators and prove that our methods are asymptotically unbiased in the infinite sample limit. This is an important improvement compared to the pooled estimator using the union of interventional and observational data, for which the bias only vanishes if the ratio of observational to interventional data tends to zero. Studies on synthetic data confirm our theoretical findings. In settings where confounding is substantial and the ratio of observational to interventional data is large, our estimators outperform a Stein-type estimator and various other baselines.

Nonparametric Identifiability of Causal Representations from Unknown Interventions

We study causal representation learning, the task of inferring latent causal variables and their causal relations from high-dimensional functions ("mixtures") of the variables. Prior work relies on weak supervision, in the form of counterfactual pre- and post-intervention views or temporal structure; places restrictive assumptions, such as linearity, on the mixing function or latent causal model; or requires partial knowledge of the generative process, such as the causal graph or the intervention targets. We instead consider the general setting in which both the causal model and the mixing function are nonparametric. The learning signal takes the form of multiple datasets, or environments, arising from unknown interventions in the underlying causal model. Our goal is to identify both the ground truth latents and their causal graph up to a set of ambiguities which we show to be irresolvable from interventional data. We study the fundamental setting of two causal variables and prove that the observational distribution and one perfect intervention per node suffice for identifiability, subject to a genericity condition. This condition rules out spurious solutions that involve fine-tuning of the intervened and observational distributions, mirroring similar conditions for nonlinear cause-effect inference. For an arbitrary number of variables, we show that two distinct paired perfect interventions per node guarantee identifiability. Further, we demonstrate that the strengths of causal influences among the latent variables are preserved by all equivalent solutions, rendering the inferred representation appropriate for drawing causal conclusions from new data. Our study provides the first identifiability results for the general nonparametric setting with unknown interventions, and elucidates what is possible and impossible for causal representation learning without more direct supervision.