Conformal Generative Modeling with Improved Sample Efficiency through Sequential Greedy Filtering

Generative models lack rigorous statistical guarantees for their outputs and are therefore unreliable in safety-critical applications. In this work, we propose Sequential Conformal Prediction for Generative Models (SCOPE-Gen), a sequential conformal prediction method producing prediction sets that satisfy a rigorous statistical guarantee called conformal admissibility control. This guarantee states that with high probability, the prediction sets contain at least one admissible (or valid) example. To this end, our method first samples an initial set of i.i.d. examples from a black box generative model. Then, this set is iteratively pruned via so-called greedy filters. As a consequence of the iterative generation procedure, admissibility of the final prediction set factorizes as a Markov chain. This factorization is crucial, because it allows to control each factor separately, using conformal prediction. In comparison to prior work, our method demonstrates a large reduction in the number of admissibility evaluations during calibration. This reduction is important in safety-critical applications, where these evaluations must be conducted manually by domain experts and are therefore costly and time consuming. We highlight the advantages of our method in terms of admissibility evaluations and cardinality of the prediction sets through experiments in natural language generation and molecular graph extension tasks.

Deep Backtracking Counterfactuals for Causally Compliant Explanations

Counterfactuals can offer valuable insights by answering what would have been observed under altered circumstances, conditional on a factual observation. Whereas the classical interventional interpretation of counterfactuals has been studied extensively, backtracking constitutes a less studied alternative the backtracking principle has emerged as an alternative philosophy where all causal laws are kept intact. In the present work, we introduce a practical method for computing backtracking counterfactuals in structural causal models that consist of deep generative components. To this end, we impose conditions on the structural assignments that enable the generation of counterfactuals by solving a tractable constrained optimization problem in the structured latent space of a causal model. Our formulation also facilitates a comparison with methods in the field of counterfactual explanations. Compared to these, our method represents a versatile, modular and causally compliant alternative. We demonstrate these properties experimentally on a modified version of MNIST and CelebA.

Causal Effect Estimation from Observational and Interventional Data Through Matrix Weighted Linear Estimators

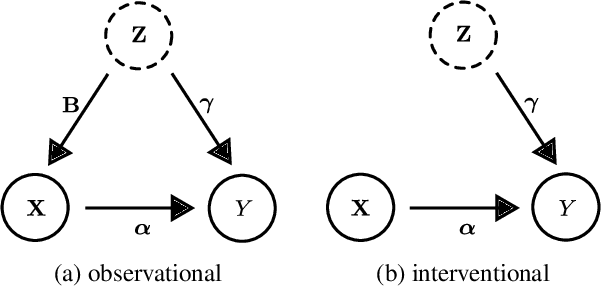
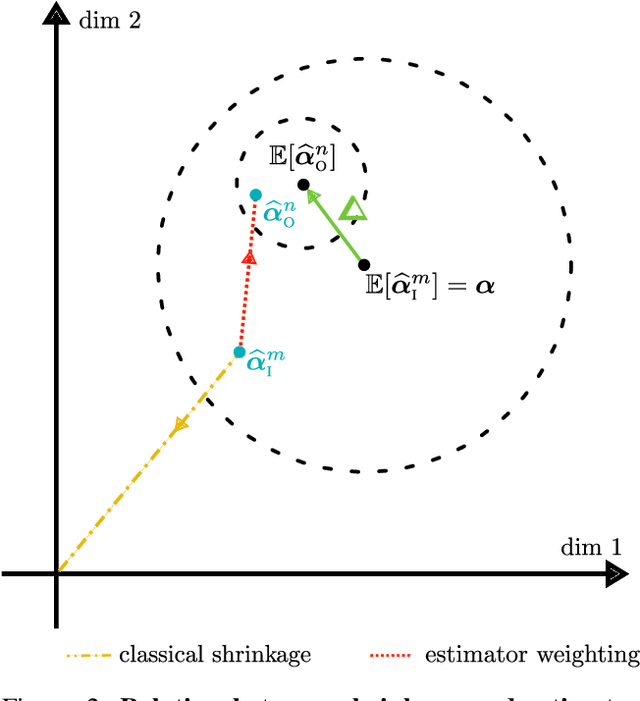
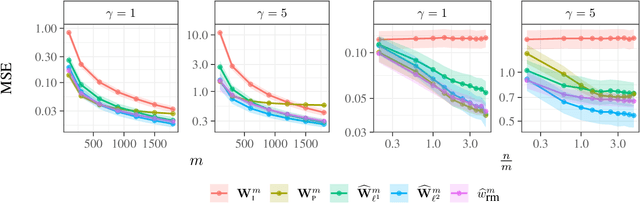
We study causal effect estimation from a mixture of observational and interventional data in a confounded linear regression model with multivariate treatments. We show that the statistical efficiency in terms of expected squared error can be improved by combining estimators arising from both the observational and interventional setting. To this end, we derive methods based on matrix weighted linear estimators and prove that our methods are asymptotically unbiased in the infinite sample limit. This is an important improvement compared to the pooled estimator using the union of interventional and observational data, for which the bias only vanishes if the ratio of observational to interventional data tends to zero. Studies on synthetic data confirm our theoretical findings. In settings where confounding is substantial and the ratio of observational to interventional data is large, our estimators outperform a Stein-type estimator and various other baselines.

Multi-agent Actor-Critic with Time Dynamical Opponent Model

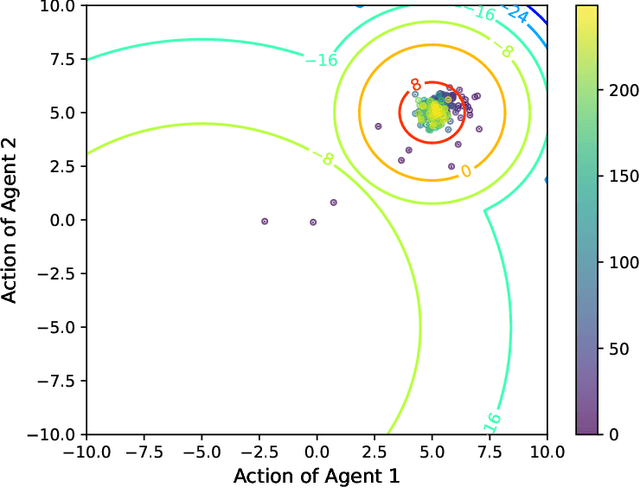
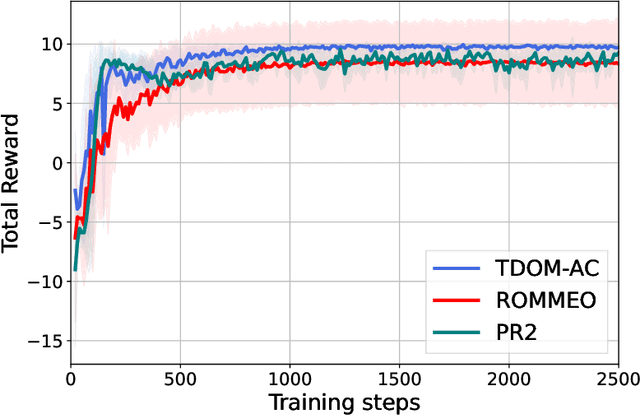
In multi-agent reinforcement learning, multiple agents learn simultaneously while interacting with a common environment and each other. Since the agents adapt their policies during learning, not only the behavior of a single agent becomes non-stationary, but also the environment as perceived by the agent. This renders it particularly challenging to perform policy improvement. In this paper, we propose to exploit the fact that the agents seek to improve their expected cumulative reward and introduce a novel \textit{Time Dynamical Opponent Model} (TDOM) to encode the knowledge that the opponent policies tend to improve over time. We motivate TDOM theoretically by deriving a lower bound of the log objective of an individual agent and further propose \textit{Multi-Agent Actor-Critic with Time Dynamical Opponent Model} (TDOM-AC). We evaluate the proposed TDOM-AC on a differential game and the Multi-agent Particle Environment. We show empirically that TDOM achieves superior opponent behavior prediction during test time. The proposed TDOM-AC methodology outperforms state-of-the-art Actor-Critic methods on the performed experiments in cooperative and \textbf{especially} in mixed cooperative-competitive environments. TDOM-AC results in a more stable training and a faster convergence.