Towards Better Generalization via Distributional Input Projection Network

As overparameterized models become increasingly prevalent, training loss alone offers limited insight into generalization performance. While smoothness has been linked to improved generalization across various settings, directly enforcing smoothness in neural networks remains challenging. To address this, we introduce Distributional Input Projection Networks (DIPNet), a novel framework that projects inputs into learnable distributions at each layer. This distributional representation induces a smoother loss landscape with respect to the input, promoting better generalization. We provide theoretical analysis showing that DIPNet reduces both local smoothness measures and the Lipschitz constant of the network, contributing to improved generalization performance. Empirically, we validate DIPNet across a wide range of architectures and tasks, including Vision Transformers (ViTs), Large Language Models (LLMs), ResNet and MLPs. Our method consistently enhances test performance under standard settings, adversarial attacks, out-of-distribution inputs, and reasoning benchmarks. We demonstrate that the proposed input projection strategy can be seamlessly integrated into existing models, providing a general and effective approach for boosting generalization performance in modern deep learning.

Causality-Inspired Robustness for Nonlinear Models via Representation Learning

Distributional robustness is a central goal of prediction algorithms due to the prevalent distribution shifts in real-world data. The prediction model aims to minimize the worst-case risk among a class of distributions, a.k.a., an uncertainty set. Causality provides a modeling framework with a rigorous robustness guarantee in the above sense, where the uncertainty set is data-driven rather than pre-specified as in traditional distributional robustness optimization. However, current causality-inspired robustness methods possess finite-radius robustness guarantees only in the linear settings, where the causal relationships among the covariates and the response are linear. In this work, we propose a nonlinear method under a causal framework by incorporating recent developments in identifiable representation learning and establish a distributional robustness guarantee. To our best knowledge, this is the first causality-inspired robustness method with such a finite-radius robustness guarantee in nonlinear settings. Empirical validation of the theoretical findings is conducted on both synthetic data and real-world single-cell data, also illustrating that finite-radius robustness is crucial.

Representation Learning for Distributional Perturbation Extrapolation

We consider the problem of modelling the effects of unseen perturbations such as gene knockdowns or drug combinations on low-level measurements such as RNA sequencing data. Specifically, given data collected under some perturbations, we aim to predict the distribution of measurements for new perturbations. To address this challenging extrapolation task, we posit that perturbations act additively in a suitable, unknown embedding space. More precisely, we formulate the generative process underlying the observed data as a latent variable model, in which perturbations amount to mean shifts in latent space and can be combined additively. Unlike previous work, we prove that, given sufficiently diverse training perturbations, the representation and perturbation effects are identifiable up to affine transformation, and use this to characterize the class of unseen perturbations for which we obtain extrapolation guarantees. To estimate the model from data, we propose a new method, the perturbation distribution autoencoder (PDAE), which is trained by maximising the distributional similarity between true and predicted perturbation distributions. The trained model can then be used to predict previously unseen perturbation distributions. Empirical evidence suggests that PDAE compares favourably to existing methods and baselines at predicting the effects of unseen perturbations.

Reverse Markov Learning: Multi-Step Generative Models for Complex Distributions

Learning complex distributions is a fundamental challenge in contemporary applications. Generative models, such as diffusion models, have demonstrated remarkable success in overcoming many limitations of traditional statistical methods. Shen and Meinshausen (2024) introduced engression, a generative approach based on scoring rules that maps noise (and covariates, if available) directly to data. While effective, engression struggles with highly complex distributions, such as those encountered in image data. In this work, we extend engression to improve its capability in learning complex distributions. We propose a framework that defines a general forward process transitioning from the target distribution to a known distribution (e.g., Gaussian) and then learns a reverse Markov process using multiple engression models. This reverse process reconstructs the target distribution step by step. Our approach supports general forward processes, allows for dimension reduction, and naturally discretizes the generative process. As a special case, when using a diffusion-based forward process, our framework offers a method to discretize the training and inference of diffusion models efficiently. Empirical evaluations on simulated and climate data validate our theoretical insights, demonstrating the effectiveness of our approach in capturing complex distributions.

Distributional Instrumental Variable Method

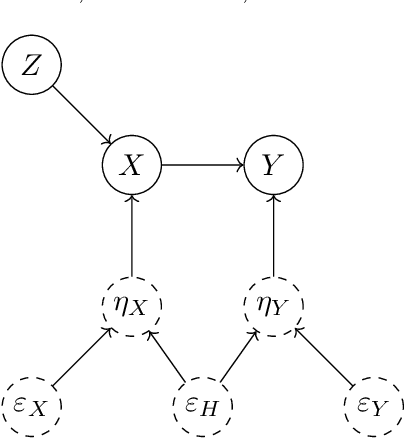
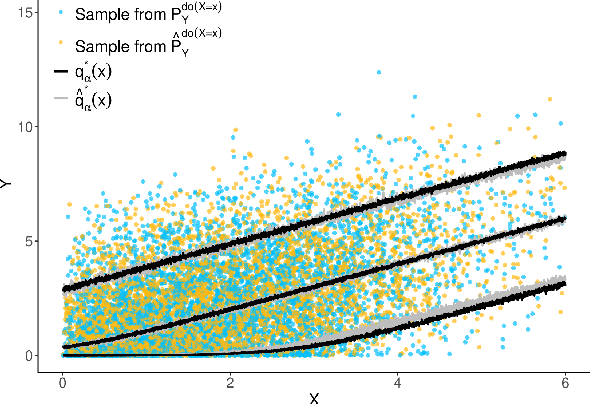
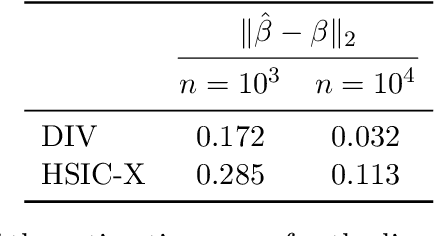
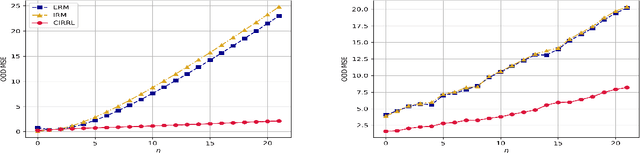
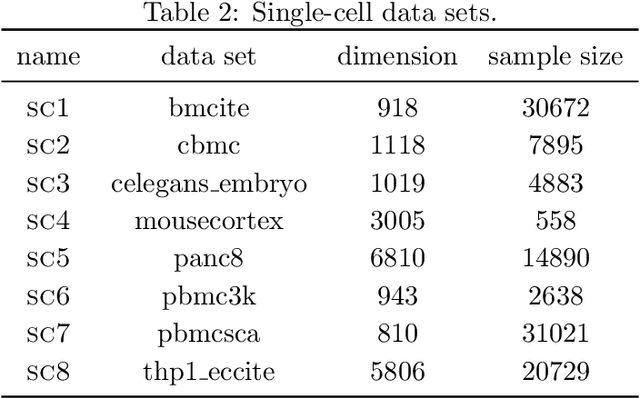
The instrumental variable (IV) approach is commonly used to infer causal effects in the presence of unmeasured confounding. Conventional IV models commonly make the additive noise assumption, which is hard to ensure in practice, but also typically lack flexibility if the causal effects are complex. Further, the vast majority of the existing methods aims to estimate the mean causal effects only, a few other methods focus on the quantile effects. This work aims for estimation of the entire interventional distribution. We propose a novel method called distributional instrumental variables (DIV), which leverages generative modelling in a nonlinear instrumental variable setting. We establish identifiability of the interventional distribution under general assumptions and demonstrate an `under-identified' case where DIV can identify the causal effects while two-step least squares fails to. Our empirical results show that the DIV method performs well for a broad range of simulated data, exhibiting advantages over existing IV approaches in terms of the identifiability and estimation error of the mean or quantile treatment effects. Furthermore, we apply DIV to an economic data set to examine the causal relation between institutional quality and economic development and our results that closely align with the original study. We also apply DIV to a single-cell data set, where we study the generalizability and stability in predicting gene expression under unseen interventions. The software implementations of DIV are available in R and Python.

Distributional Principal Autoencoders

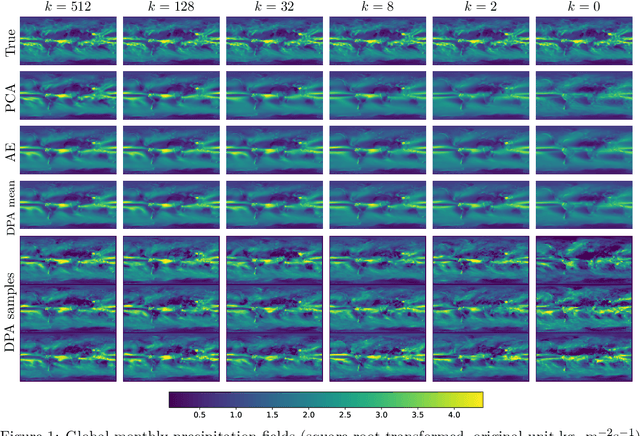
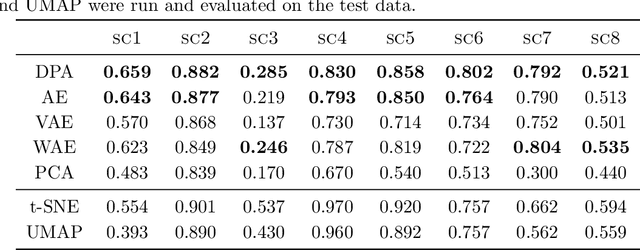
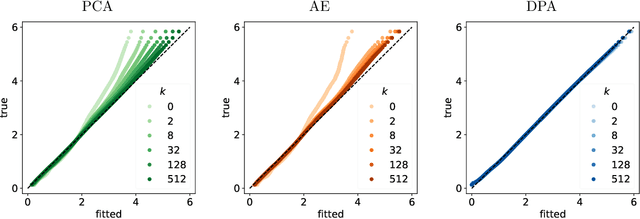
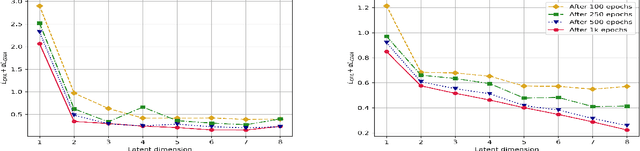
Dimension reduction techniques usually lose information in the sense that reconstructed data are not identical to the original data. However, we argue that it is possible to have reconstructed data identically distributed as the original data, irrespective of the retained dimension or the specific mapping. This can be achieved by learning a distributional model that matches the conditional distribution of data given its low-dimensional latent variables. Motivated by this, we propose Distributional Principal Autoencoder (DPA) that consists of an encoder that maps high-dimensional data to low-dimensional latent variables and a decoder that maps the latent variables back to the data space. For reducing the dimension, the DPA encoder aims to minimise the unexplained variability of the data with an adaptive choice of the latent dimension. For reconstructing data, the DPA decoder aims to match the conditional distribution of all data that are mapped to a certain latent value, thus ensuring that the reconstructed data retains the original data distribution. Our numerical results on climate data, single-cell data, and image benchmarks demonstrate the practical feasibility and success of the approach in reconstructing the original distribution of the data. DPA embeddings are shown to preserve meaningful structures of data such as the seasonal cycle for precipitations and cell types for gene expression.

Invariant Probabilistic Prediction

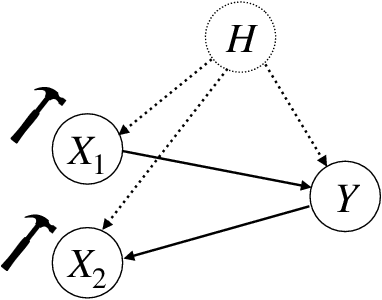
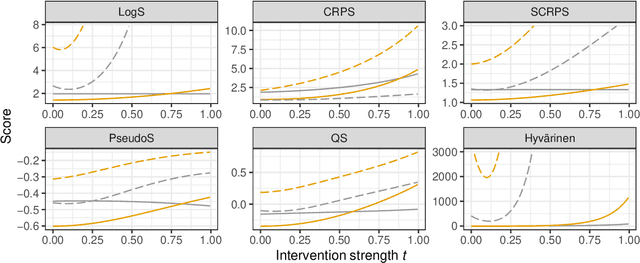
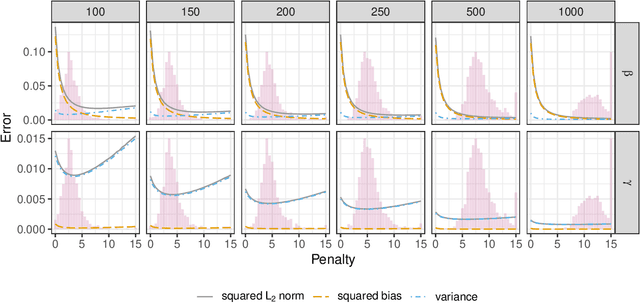
In recent years, there has been a growing interest in statistical methods that exhibit robust performance under distribution changes between training and test data. While most of the related research focuses on point predictions with the squared error loss, this article turns the focus towards probabilistic predictions, which aim to comprehensively quantify the uncertainty of an outcome variable given covariates. Within a causality-inspired framework, we investigate the invariance and robustness of probabilistic predictions with respect to proper scoring rules. We show that arbitrary distribution shifts do not, in general, admit invariant and robust probabilistic predictions, in contrast to the setting of point prediction. We illustrate how to choose evaluation metrics and restrict the class of distribution shifts to allow for identifiability and invariance in the prototypical Gaussian heteroscedastic linear model. Motivated by these findings, we propose a method to yield invariant probabilistic predictions, called IPP, and study the consistency of the underlying parameters. Finally, we demonstrate the empirical performance of our proposed procedure on simulated as well as on single-cell data.

Causality-oriented robustness: exploiting general additive interventions

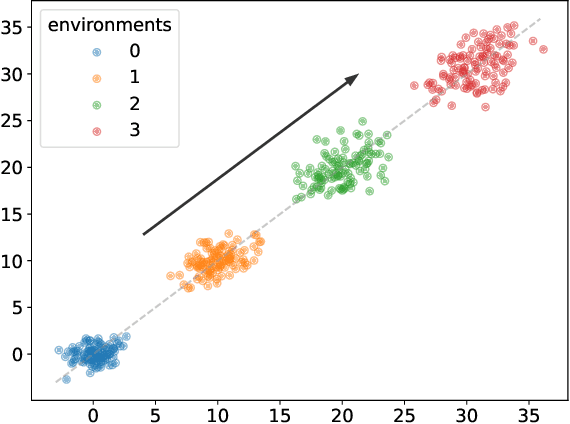
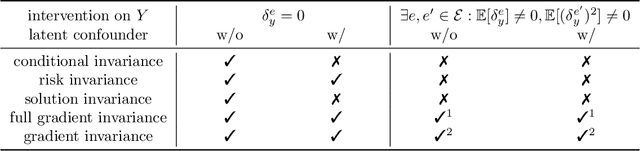
Since distribution shifts are common in real-world applications, there is a pressing need for developing prediction models that are robust against such shifts. Existing frameworks, such as empirical risk minimization or distributionally robust optimization, either lack generalizability for unseen distributions or rely on postulated distance measures. Alternatively, causality offers a data-driven and structural perspective to robust predictions. However, the assumptions necessary for causal inference can be overly stringent, and the robustness offered by such causal models often lacks flexibility. In this paper, we focus on causality-oriented robustness and propose Distributional Robustness via Invariant Gradients (DRIG), a method that exploits general additive interventions in training data for robust predictions against unseen interventions, and naturally interpolates between in-distribution prediction and causality. In a linear setting, we prove that DRIG yields predictions that are robust among a data-dependent class of distribution shifts. Furthermore, we show that our framework includes anchor regression (Rothenh\"ausler et al.\ 2021) as a special case, and that it yields prediction models that protect against more diverse perturbations. We extend our approach to the semi-supervised domain adaptation setting to further improve prediction performance. Finally, we empirically validate our methods on synthetic simulations and on single-cell data.

Engression: Extrapolation for Nonlinear Regression?

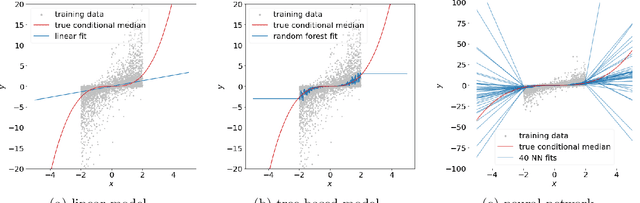
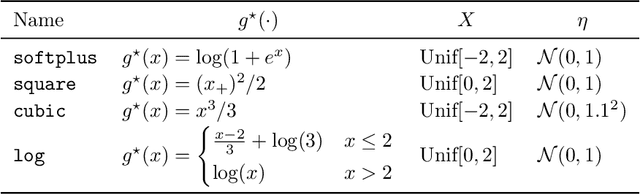
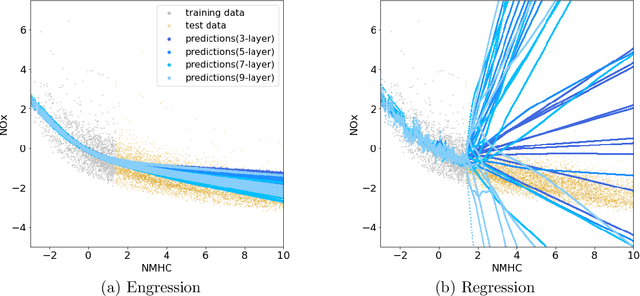
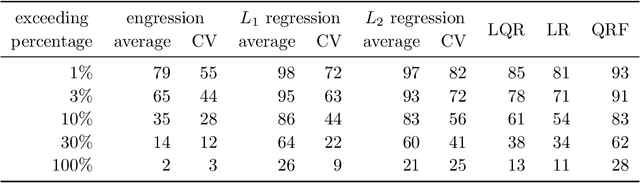
Extrapolation is crucial in many statistical and machine learning applications, as it is common to encounter test data outside the training support. However, extrapolation is a considerable challenge for nonlinear models. Conventional models typically struggle in this regard: while tree ensembles provide a constant prediction beyond the support, neural network predictions tend to become uncontrollable. This work aims at providing a nonlinear regression methodology whose reliability does not break down immediately at the boundary of the training support. Our primary contribution is a new method called `engression' which, at its core, is a distributional regression technique for pre-additive noise models, where the noise is added to the covariates before applying a nonlinear transformation. Our experimental results indicate that this model is typically suitable for many real data sets. We show that engression can successfully perform extrapolation under some assumptions such as a strictly monotone function class, whereas traditional regression approaches such as least-squares regression and quantile regression fall short under the same assumptions. We establish the advantages of engression over existing approaches in terms of extrapolation, showing that engression consistently provides a meaningful improvement. Our empirical results, from both simulated and real data, validate these findings, highlighting the effectiveness of the engression method. The software implementations of engression are available in both R and Python.

Asymptotic Statistical Analysis of $f$-divergence GAN

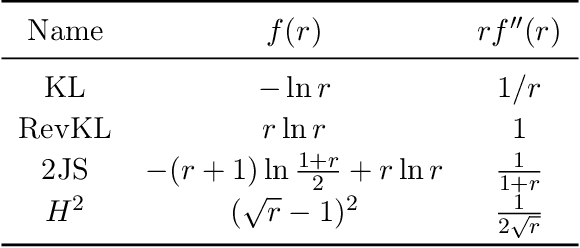
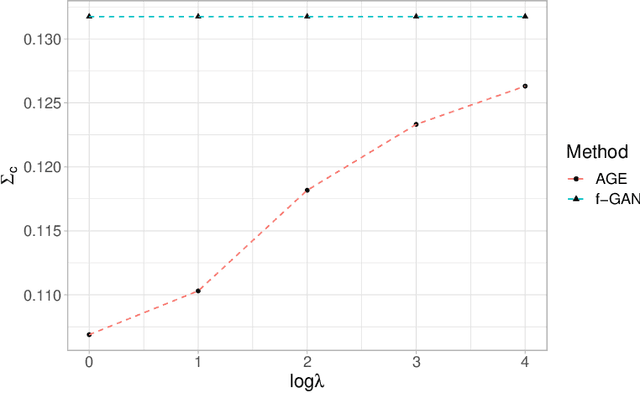
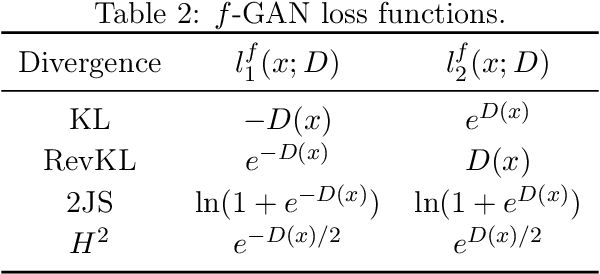
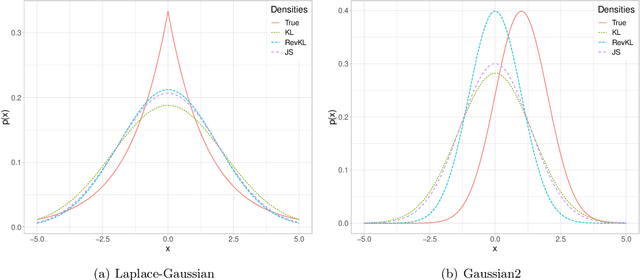
Generative Adversarial Networks (GANs) have achieved great success in data generation. However, its statistical properties are not fully understood. In this paper, we consider the statistical behavior of the general $f$-divergence formulation of GAN, which includes the Kullback--Leibler divergence that is closely related to the maximum likelihood principle. We show that for parametric generative models that are correctly specified, all $f$-divergence GANs with the same discriminator classes are asymptotically equivalent under suitable regularity conditions. Moreover, with an appropriately chosen local discriminator, they become equivalent to the maximum likelihood estimate asymptotically. For generative models that are misspecified, GANs with different $f$-divergences {converge to different estimators}, and thus cannot be directly compared. However, it is shown that for some commonly used $f$-divergences, the original $f$-GAN is not optimal in that one can achieve a smaller asymptotic variance when the discriminator training in the original $f$-GAN formulation is replaced by logistic regression. The resulting estimation method is referred to as Adversarial Gradient Estimation (AGE). Empirical studies are provided to support the theory and to demonstrate the advantage of AGE over the original $f$-GANs under model misspecification.