Sorawit Saengkyongam
Hybrid Modeling of Photoplethysmography for Non-invasive Monitoring of Cardiovascular Parameters
Nov 18, 2025Abstract:Continuous cardiovascular monitoring can play a key role in precision health. However, some fundamental cardiac biomarkers of interest, including stroke volume and cardiac output, require invasive measurements, e.g., arterial pressure waveforms (APW). As a non-invasive alternative, photoplethysmography (PPG) measurements are routinely collected in hospital settings. Unfortunately, the prediction of key cardiac biomarkers from PPG instead of APW remains an open challenge, further complicated by the scarcity of annotated PPG measurements. As a solution, we propose a hybrid approach that uses hemodynamic simulations and unlabeled clinical data to estimate cardiovascular biomarkers directly from PPG signals. Our hybrid model combines a conditional variational autoencoder trained on paired PPG-APW data with a conditional density estimator of cardiac biomarkers trained on labeled simulated APW segments. As a key result, our experiments demonstrate that the proposed approach can detect fluctuations of cardiac output and stroke volume and outperform a supervised baseline in monitoring temporal changes in these biomarkers.
Distributional Instrumental Variable Method
Feb 11, 2025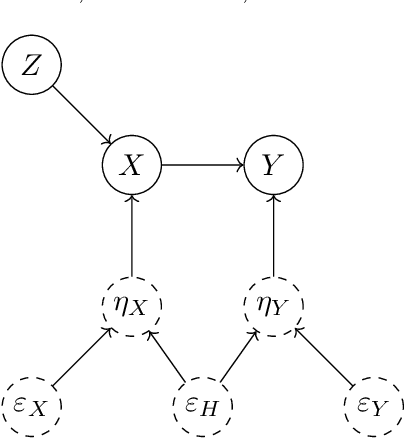

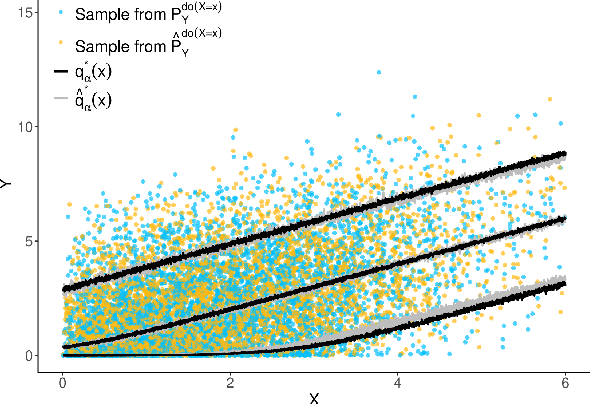
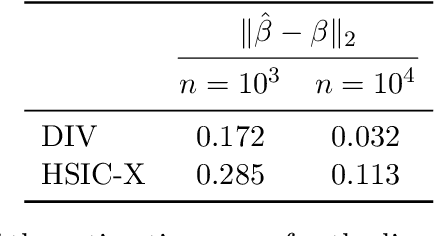
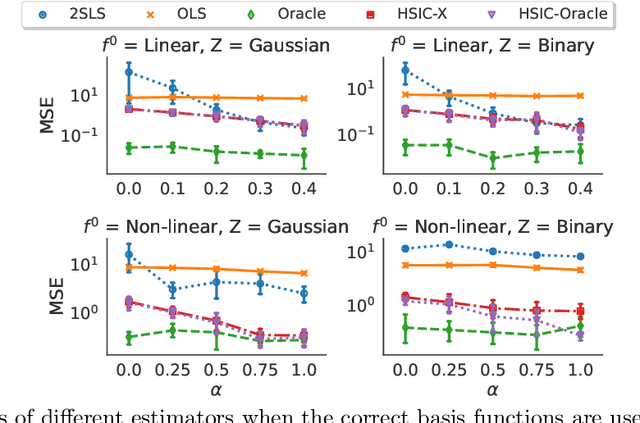
Abstract:The instrumental variable (IV) approach is commonly used to infer causal effects in the presence of unmeasured confounding. Conventional IV models commonly make the additive noise assumption, which is hard to ensure in practice, but also typically lack flexibility if the causal effects are complex. Further, the vast majority of the existing methods aims to estimate the mean causal effects only, a few other methods focus on the quantile effects. This work aims for estimation of the entire interventional distribution. We propose a novel method called distributional instrumental variables (DIV), which leverages generative modelling in a nonlinear instrumental variable setting. We establish identifiability of the interventional distribution under general assumptions and demonstrate an `under-identified' case where DIV can identify the causal effects while two-step least squares fails to. Our empirical results show that the DIV method performs well for a broad range of simulated data, exhibiting advantages over existing IV approaches in terms of the identifiability and estimation error of the mean or quantile treatment effects. Furthermore, we apply DIV to an economic data set to examine the causal relation between institutional quality and economic development and our results that closely align with the original study. We also apply DIV to a single-cell data set, where we study the generalizability and stability in predicting gene expression under unseen interventions. The software implementations of DIV are available in R and Python.
Identifying Representations for Intervention Extrapolation
Oct 06, 2023



Abstract:The premise of identifiable and causal representation learning is to improve the current representation learning paradigm in terms of generalizability or robustness. Despite recent progress in questions of identifiability, more theoretical results demonstrating concrete advantages of these methods for downstream tasks are needed. In this paper, we consider the task of intervention extrapolation: predicting how interventions affect an outcome, even when those interventions are not observed at training time, and show that identifiable representations can provide an effective solution to this task even if the interventions affect the outcome non-linearly. Our setup includes an outcome Y, observed features X, which are generated as a non-linear transformation of latent features Z, and exogenous action variables A, which influence Z. The objective of intervention extrapolation is to predict how interventions on A that lie outside the training support of A affect Y. Here, extrapolation becomes possible if the effect of A on Z is linear and the residual when regressing Z on A has full support. As Z is latent, we combine the task of intervention extrapolation with identifiable representation learning, which we call Rep4Ex: we aim to map the observed features X into a subspace that allows for non-linear extrapolation in A. We show using Wiener's Tauberian theorem that the hidden representation is identifiable up to an affine transformation in Z-space, which is sufficient for intervention extrapolation. The identifiability is characterized by a novel constraint describing the linearity assumption of A on Z. Based on this insight, we propose a method that enforces the linear invariance constraint and can be combined with any type of autoencoder. We validate our theoretical findings through synthetic experiments and show that our approach succeeds in predicting the effects of unseen interventions.
Model-based causal feature selection for general response types
Sep 22, 2023Abstract:Discovering causal relationships from observational data is a fundamental yet challenging task. In some applications, it may suffice to learn the causal features of a given response variable, instead of learning the entire underlying causal structure. Invariant causal prediction (ICP, Peters et al., 2016) is a method for causal feature selection which requires data from heterogeneous settings. ICP assumes that the mechanism for generating the response from its direct causes is the same in all settings and exploits this invariance to output a subset of the causal features. The framework of ICP has been extended to general additive noise models and to nonparametric settings using conditional independence testing. However, nonparametric conditional independence testing often suffers from low power (or poor type I error control) and the aforementioned parametric models are not suitable for applications in which the response is not measured on a continuous scale, but rather reflects categories or counts. To bridge this gap, we develop ICP in the context of transformation models (TRAMs), allowing for continuous, categorical, count-type, and uninformatively censored responses (we show that, in general, these model classes do not allow for identifiability when there is no exogenous heterogeneity). We propose TRAM-GCM, a test for invariance of a subset of covariates, based on the expected conditional covariance between environments and score residuals which satisfies uniform asymptotic level guarantees. For the special case of linear shift TRAMs, we propose an additional invariance test, TRAM-Wald, based on the Wald statistic. We implement both proposed methods in the open-source R package "tramicp" and show in simulations that under the correct model specification, our approach empirically yields higher power than nonparametric ICP based on conditional independence testing.
Effect-Invariant Mechanisms for Policy Generalization
Jun 27, 2023Abstract:Policy learning is an important component of many real-world learning systems. A major challenge in policy learning is how to adapt efficiently to unseen environments or tasks. Recently, it has been suggested to exploit invariant conditional distributions to learn models that generalize better to unseen environments. However, assuming invariance of entire conditional distributions (which we call full invariance) may be too strong of an assumption in practice. In this paper, we introduce a relaxation of full invariance called effect-invariance (e-invariance for short) and prove that it is sufficient, under suitable assumptions, for zero-shot policy generalization. We also discuss an extension that exploits e-invariance when we have a small sample from the test environment, enabling few-shot policy generalization. Our work does not assume an underlying causal graph or that the data are generated by a structural causal model; instead, we develop testing procedures to test e-invariance directly from data. We present empirical results using simulated data and a mobile health intervention dataset to demonstrate the effectiveness of our approach.
Exploiting Independent Instruments: Identification and Distribution Generalization
Feb 03, 2022
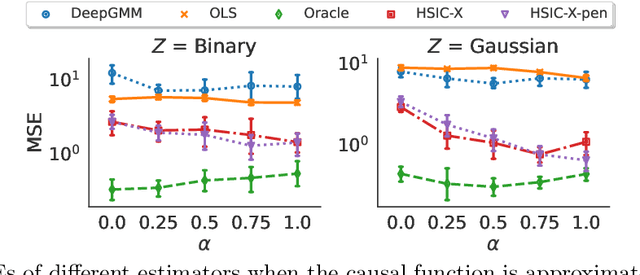
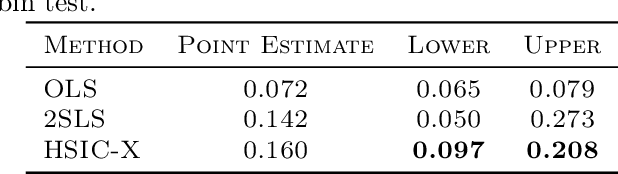
Abstract:Instrumental variable models allow us to identify a causal function between covariates X and a response Y, even in the presence of unobserved confounding. Most of the existing estimators assume that the error term in the response Y and the hidden confounders are uncorrelated with the instruments Z. This is often motivated by a graphical separation, an argument that also justifies independence. Posing an independence condition, however, leads to strictly stronger identifiability results. We connect to existing literature in econometrics and provide a practical method for exploiting independence that can be combined with any gradient-based learning procedure. We see that even in identifiable settings, taking into account higher moments may yield better finite sample results. Furthermore, we exploit the independence for distribution generalization. We prove that the proposed estimator is invariant to distributional shifts on the instruments and worst-case optimal whenever these shifts are sufficiently strong. These results hold even in the under-identified case where the instruments are not sufficiently rich to identify the causal function.
Invariant Policy Learning: A Causal Perspective
Jun 07, 2021



Abstract:In the past decade, contextual bandit and reinforcement learning algorithms have been successfully used in various interactive learning systems such as online advertising, recommender systems, and dynamic pricing. However, they have yet to be widely adopted in high-stakes application domains, such as healthcare. One reason may be that existing approaches assume that the underlying mechanisms are static in the sense that they do not change over time or over different environments. In many real world systems, however, the mechanisms are subject to shifts across environments which may invalidate the static environment assumption. In this paper, we tackle the problem of environmental shifts under the framework of offline contextual bandits. We view the environmental shift problem through the lens of causality and propose multi-environment contextual bandits that allow for changes in the underlying mechanisms. We adopt the concept of invariance from the causality literature and introduce the notion of policy invariance. We argue that policy invariance is only relevant if unobserved confounders are present and show that, in that case, an optimal invariant policy is guaranteed, under certain assumptions, to generalize across environments. Our results do not only provide a solution to the environmental shift problem but also establish concrete connections among causality, invariance and contextual bandits.
Learning Joint Nonlinear Effects from Single-variable Interventions in the Presence of Hidden Confounders
Jun 16, 2020



Abstract:We propose an approach to estimate the effect of multiple simultaneous interventions in the presence of hidden confounders. To overcome the problem of hidden confounding, we consider the setting where we have access to not only the observational data but also sets of single-variable interventions in which each of the treatment variables is intervened on separately. We prove identifiability under the assumption that the data is generated from a nonlinear continuous structural causal model with additive Gaussian noise. In addition, we propose a simple parameter estimation method by pooling all the data from different regimes and jointly maximizing the combined likelihood. We also conduct comprehensive experiments to verify the identifiability result as well as to compare the performance of our approach against a baseline on both synthetic and real-world data.
Counterfactual Mean Embedding: A Kernel Method for Nonparametric Causal Inference
May 22, 2018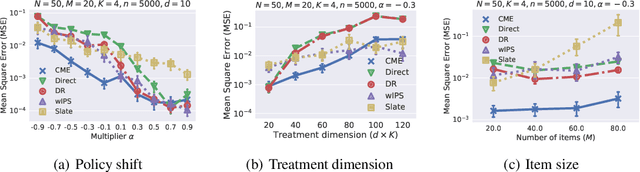
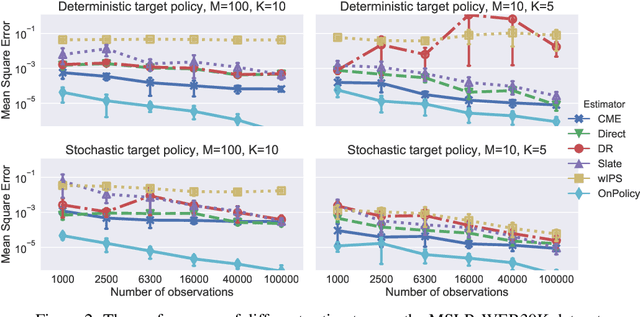
Abstract:This paper introduces a novel Hilbert space representation of a counterfactual distribution---called counterfactual mean embedding (CME)---with applications in nonparametric causal inference. Counterfactual prediction has become an ubiquitous tool in machine learning applications, such as online advertisement, recommendation systems, and medical diagnosis, whose performance relies on certain interventions. To infer the outcomes of such interventions, we propose to embed the associated counterfactual distribution into a reproducing kernel Hilbert space (RKHS) endowed with a positive definite kernel. Under appropriate assumptions, the CME allows us to perform causal inference over the entire landscape of the counterfactual distribution. The CME can be estimated consistently from observational data without requiring any parametric assumption about the underlying distributions. We also derive a rate of convergence which depends on the smoothness of the conditional mean and the Radon-Nikodym derivative of the underlying marginal distributions. Our framework can deal with not only real-valued outcome, but potentially also more complex and structured outcomes such as images, sequences, and graphs. Lastly, our experimental results on off-policy evaluation tasks demonstrate the advantages of the proposed estimator.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge