Variable Selection for Comparing High-dimensional Time-Series Data

Given a pair of multivariate time-series data of the same length and dimensions, an approach is proposed to select variables and time intervals where the two series are significantly different. In applications where one time series is an output from a computationally expensive simulator, the approach may be used for validating the simulator against real data, for comparing the outputs of two simulators, and for validating a machine learning-based emulator against the simulator. With the proposed approach, the entire time interval is split into multiple subintervals, and on each subinterval, the two sample sets are compared to select variables that distinguish their distributions and a two-sample test is performed. The validity and limitations of the proposed approach are investigated in synthetic data experiments. Its usefulness is demonstrated in an application with a particle-based fluid simulator, where a deep neural network model is compared against the simulator, and in an application with a microscopic traffic simulator, where the effects of changing the simulator's parameters on traffic flows are analysed.

Fast Computation of Leave-One-Out Cross-Validation for $k$-NN Regression

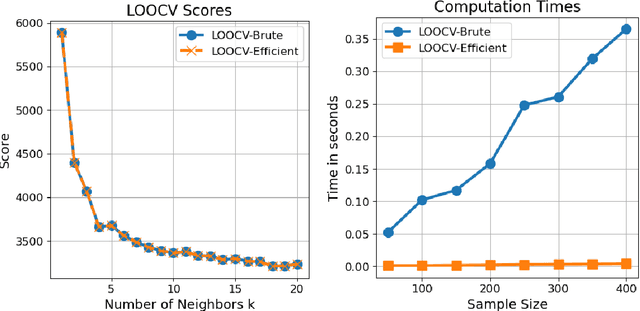
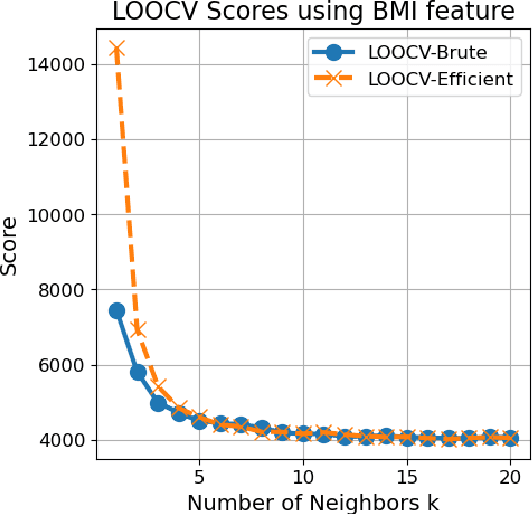
We describe a fast computation method for leave-one-out cross-validation (LOOCV) for $k$-nearest neighbours ($k$-NN) regression. We show that, under a tie-breaking condition for nearest neighbours, the LOOCV estimate of the mean square error for $k$-NN regression is identical to the mean square error of $(k+1)$-NN regression evaluated on the training data, multiplied by the scaling factor $(k+1)^2/k^2$. Therefore, to compute the LOOCV score, one only needs to fit $(k+1)$-NN regression only once, and does not need to repeat training-validation of $k$-NN regression for the number of training data. Numerical experiments confirm the validity of the fast computation method.

Variable Selection in Maximum Mean Discrepancy for Interpretable Distribution Comparison

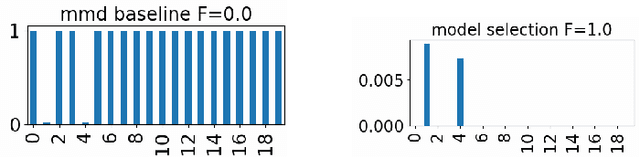
Two-sample testing decides whether two datasets are generated from the same distribution. This paper studies variable selection for two-sample testing, the task being to identify the variables (or dimensions) responsible for the discrepancies between the two distributions. This task is relevant to many problems of pattern analysis and machine learning, such as dataset shift adaptation, causal inference and model validation. Our approach is based on a two-sample test based on the Maximum Mean Discrepancy (MMD). We optimise the Automatic Relevance Detection (ARD) weights defined for individual variables to maximise the power of the MMD-based test. For this optimisation, we introduce sparse regularisation and propose two methods for dealing with the issue of selecting an appropriate regularisation parameter. One method determines the regularisation parameter in a data-driven way, and the other aggregates the results of different regularisation parameters. We confirm the validity of the proposed methods by systematic comparisons with baseline methods, and demonstrate their usefulness in exploratory analysis of high-dimensional traffic simulation data. Preliminary theoretical analyses are also provided, including a rigorous definition of variable selection for two-sample testing.

When is Importance Weighting Correction Needed for Covariate Shift Adaptation?

This paper investigates when the importance weighting (IW) correction is needed to address covariate shift, a common situation in supervised learning where the input distributions of training and test data differ. Classic results show that the IW correction is needed when the model is parametric and misspecified. In contrast, recent results indicate that the IW correction may not be necessary when the model is nonparametric and well-specified. We examine the missing case in the literature where the model is nonparametric and misspecified, and show that the IW correction is needed for obtaining the best approximation of the true unknown function for the test distribution. We do this by analyzing IW-corrected kernel ridge regression, covering a variety of settings, including parametric and nonparametric models, well-specified and misspecified settings, and arbitrary weighting functions.

Improved Random Features for Dot Product Kernels

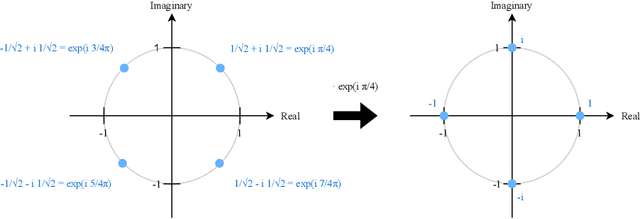
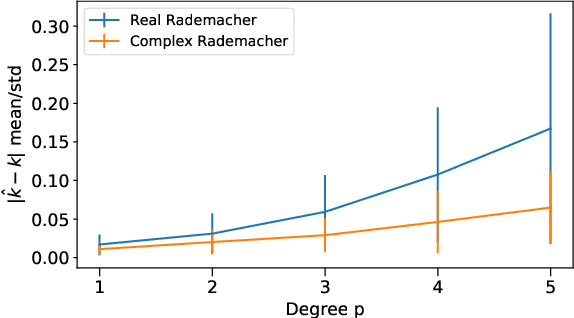
Dot product kernels, such as polynomial and exponential (softmax) kernels, are among the most widely used kernels in machine learning, as they enable modeling the interactions between input features, which is crucial in applications like computer vision, natural language processing, and recommender systems. We make several novel contributions for improving the efficiency of random feature approximations for dot product kernels, to make these kernels more useful in large scale learning. First, we present a generalization of existing random feature approximations for polynomial kernels, such as Rademacher and Gaussian sketches and TensorSRHT, using complex-valued random features. We show empirically that the use of complex features can significantly reduce the variances of these approximations. Second, we provide a theoretical analysis for understanding the factors affecting the efficiency of various random feature approximations, by deriving closed-form expressions for their variances. These variance formulas elucidate conditions under which certain approximations (e.g., TensorSRHT) achieve lower variances than others (e.g., Rademacher sketches), and conditions under which the use of complex features leads to lower variances than real features. Third, by using these variance formulas, which can be evaluated in practice, we develop a data-driven optimization approach to improve random feature approximations for general dot product kernels, which is also applicable to the Gaussian kernel. We describe the improvements brought by these contributions with extensive experiments on a variety of tasks and datasets.

Connections and Equivalences between the Nyström Method and Sparse Variational Gaussian Processes

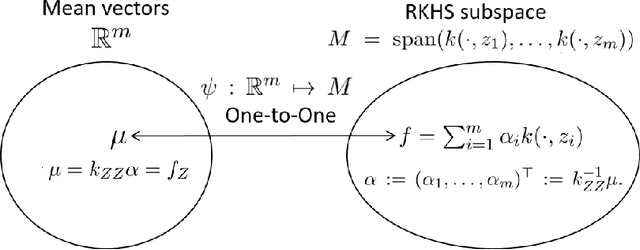
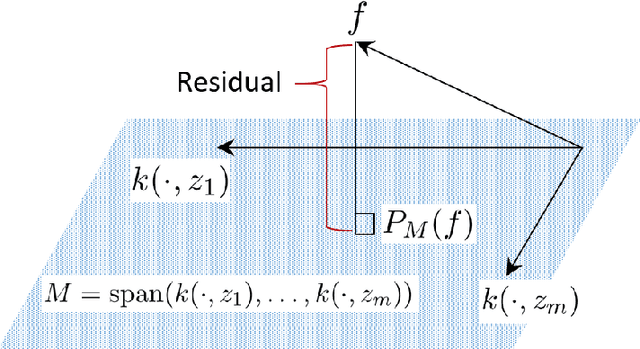
We investigate the connections between sparse approximation methods for making kernel methods and Gaussian processes (GPs) scalable to massive data, focusing on the Nystr\"om method and the Sparse Variational Gaussian Processes (SVGP). While sparse approximation methods for GPs and kernel methods share some algebraic similarities, the literature lacks a deep understanding of how and why they are related. This is a possible obstacle for the communications between the GP and kernel communities, making it difficult to transfer results from one side to the other. Our motivation is to remove this possible obstacle, by clarifying the connections between the sparse approximations for GPs and kernel methods. In this work, we study the two popular approaches, the Nystr\"om and SVGP approximations, in the context of a regression problem, and establish various connections and equivalences between them. In particular, we provide an RKHS interpretation of the SVGP approximation, and show that the Evidence Lower Bound of the SVGP contains the objective function of the Nystr\"om approximation, revealing the origin of the algebraic equivalence between the two approaches. We also study recently established convergence results for the SVGP and how they are related to the approximation quality of the Nystr\"om method.

Convergence Guarantees for Adaptive Bayesian Quadrature Methods

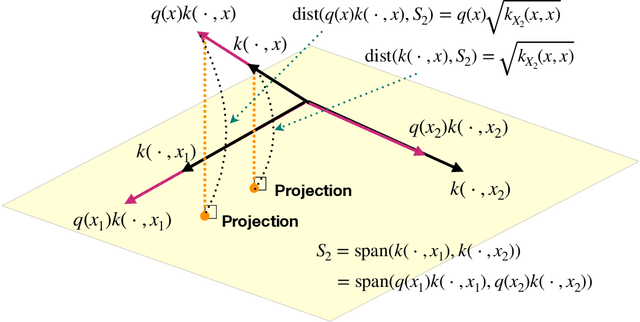
Adaptive Bayesian quadrature (ABQ) is a powerful approach to numerical integration that empirically compares favorably with Monte Carlo integration on problems of medium dimensionality (where non-adaptive quadrature is not competitive). Its key ingredient is an acquisition function that changes as a function of previously collected values of the integrand. While this adaptivity appears to be empirically powerful, it complicates analysis. Consequently, there are no theoretical guarantees so far for this class of methods. In this work, for a broad class of adaptive Bayesian quadrature methods, we prove consistency, deriving non-tight but informative convergence rates. To do so we introduce a new concept we call weak adaptivity. In guaranteeing consistency of ABQ, weak adaptivity is notionally similar to the ideas of detailed balance and ergodicity in Markov Chain Monte Carlo methods, which allow sufficient conditions for consistency of MCMC. Likewise, our results identify a large and flexible class of adaptive Bayesian quadrature rules as consistent, within which practitioners can develop empirically efficient methods.

Model Selection for Simulator-based Statistical Models: A Kernel Approach

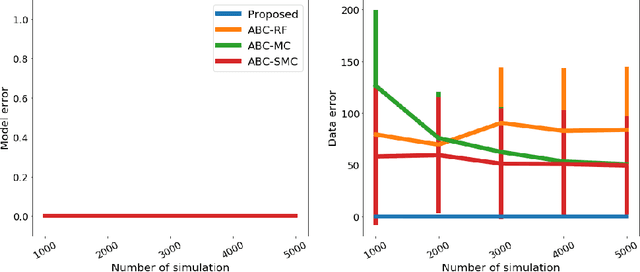
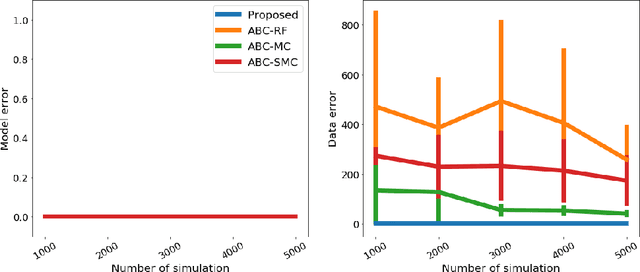
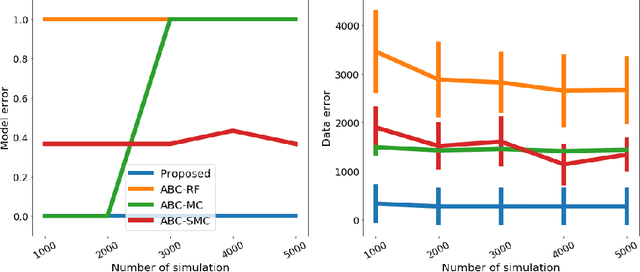
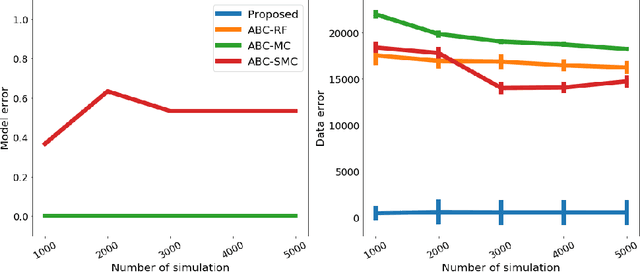
We propose a novel approach to model selection for simulator-based statistical models. The proposed approach defines a mixture of candidate models, and then iteratively updates the weight coefficients for those models as well as the parameters in each model simultaneously; this is done by recursively applying Bayes' rule, using the recently proposed kernel recursive ABC algorithm. The practical advantage of the method is that it can be used even when a modeler lacks appropriate prior knowledge about the parameters in each model. We demonstrate the effectiveness of the proposed approach with a number of experiments, including model selection for dynamical systems in ecology and epidemiology.

Large sample analysis of the median heuristic

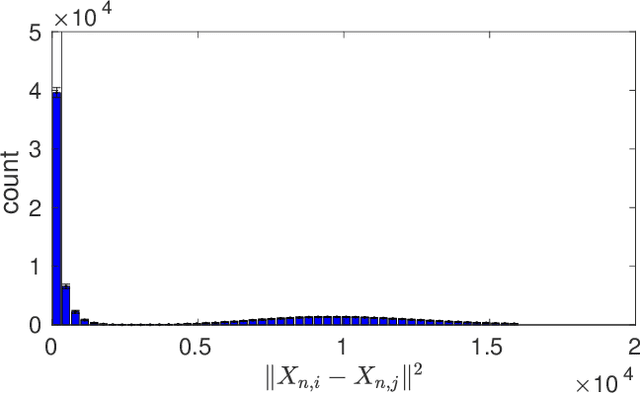
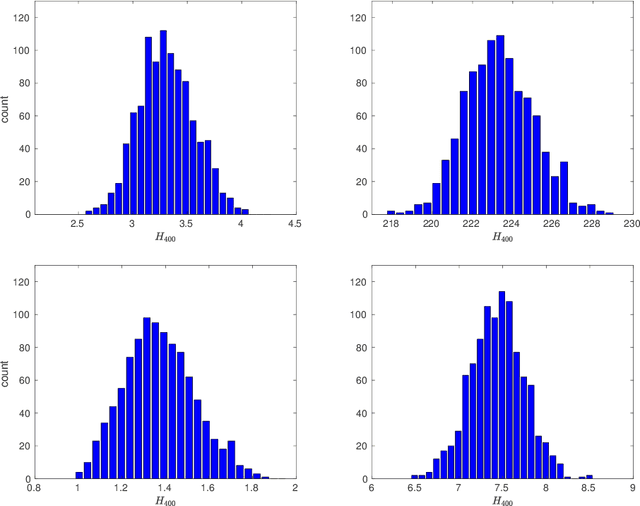
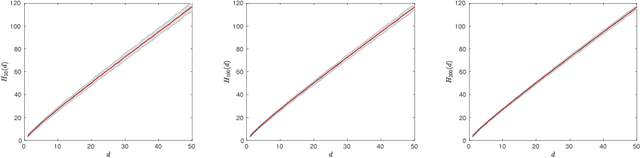
In kernel methods, the median heuristic has been widely used as a way of setting the bandwidth of RBF kernels. While its empirical performances make it a safe choice under many circumstances, there is little theoretical understanding of why this is the case. Our aim in this paper is to advance our understanding of the median heuristic by focusing on the setting of kernel two-sample test. We collect new findings that may be of interest for both theoreticians and practitioners. In theory, we provide a convergence analysis that shows the asymptotic normality of the bandwidth chosen by the median heuristic in the setting of kernel two-sample test. Systematic empirical investigations are also conducted in simple settings, comparing the performances based on the bandwidths chosen by the median heuristic and those by the maximization of test power.

Gaussian Processes and Kernel Methods: A Review on Connections and Equivalences

This paper is an attempt to bridge the conceptual gaps between researchers working on the two widely used approaches based on positive definite kernels: Bayesian learning or inference using Gaussian processes on the one side, and frequentist kernel methods based on reproducing kernel Hilbert spaces on the other. It is widely known in machine learning that these two formalisms are closely related; for instance, the estimator of kernel ridge regression is identical to the posterior mean of Gaussian process regression. However, they have been studied and developed almost independently by two essentially separate communities, and this makes it difficult to seamlessly transfer results between them. Our aim is to overcome this potential difficulty. To this end, we review several old and new results and concepts from either side, and juxtapose algorithmic quantities from each framework to highlight close similarities. We also provide discussions on subtle philosophical and theoretical differences between the two approaches.