When is Importance Weighting Correction Needed for Covariate Shift Adaptation?

This paper investigates when the importance weighting (IW) correction is needed to address covariate shift, a common situation in supervised learning where the input distributions of training and test data differ. Classic results show that the IW correction is needed when the model is parametric and misspecified. In contrast, recent results indicate that the IW correction may not be necessary when the model is nonparametric and well-specified. We examine the missing case in the literature where the model is nonparametric and misspecified, and show that the IW correction is needed for obtaining the best approximation of the true unknown function for the test distribution. We do this by analyzing IW-corrected kernel ridge regression, covering a variety of settings, including parametric and nonparametric models, well-specified and misspecified settings, and arbitrary weighting functions.

Estimating the minimizer and the minimum value of a regression function under passive design

We propose a new method for estimating the minimizer $\boldsymbol{x}^*$ and the minimum value $f^*$ of a smooth and strongly convex regression function $f$ from the observations contaminated by random noise. Our estimator $\boldsymbol{z}_n$ of the minimizer $\boldsymbol{x}^*$ is based on a version of the projected gradient descent with the gradient estimated by a regularized local polynomial algorithm. Next, we propose a two-stage procedure for estimation of the minimum value $f^*$ of regression function $f$. At the first stage, we construct an accurate enough estimator of $\boldsymbol{x}^*$, which can be, for example, $\boldsymbol{z}_n$. At the second stage, we estimate the function value at the point obtained in the first stage using a rate optimal nonparametric procedure. We derive non-asymptotic upper bounds for the quadratic risk and optimization error of $\boldsymbol{z}_n$, and for the risk of estimating $f^*$. We establish minimax lower bounds showing that, under certain choice of parameters, the proposed algorithms achieve the minimax optimal rates of convergence on the class of smooth and strongly convex functions.

Locally Smoothed Gaussian Process Regression

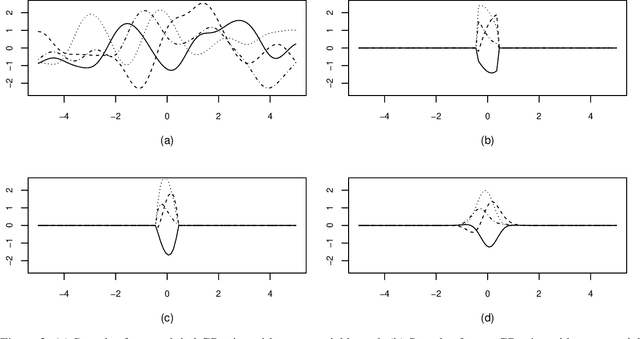
We develop a novel framework to accelerate Gaussian process regression (GPR). In particular, we consider localization kernels at each data point to down-weigh the contributions from other data points that are far away, and we derive the GPR model stemming from the application of such localization operation. Through a set of experiments, we demonstrate the competitive performance of the proposed approach compared to full GPR, other localized models, and deep Gaussian processes. Crucially, these performances are obtained with considerable speedups compared to standard global GPR due to the sparsification effect of the Gram matrix induced by the localization operation.

Importance Weighting Correction of Regularized Least-Squares for Covariate and Target Shifts

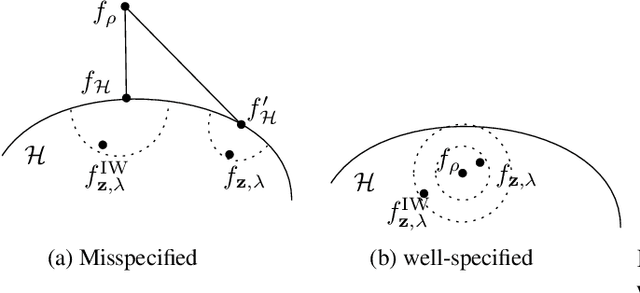
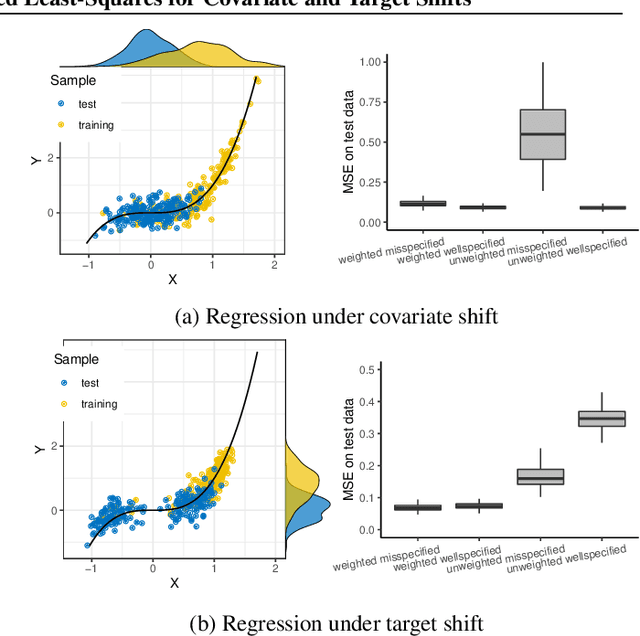
In many real world problems, the training data and test data have different distributions. This situation is commonly referred as a dataset shift. The most common settings for dataset shift often considered in the literature are {\em covariate shift } and {\em target shift}. Importance weighting (IW) correction is a universal method for correcting the bias present in learning scenarios under dataset shift. The question one may ask is: does IW correction work equally well for different dataset shift scenarios? By investigating the generalization properties of the weighted kernel ridge regression (W-KRR) under covariate and target shifts we show that the answer is negative, except when IW is bounded and the model is wellspecified. In the latter cases, a minimax optimal rates are achieved by importance weighted kernel ridge regression (IW-KRR) in both, covariate and target shift scenarios. Slightly relaxing the boundedness condition of the IW we show that the IW-KRR still achieves the optimal rates under target shift while leading to slower rates for covariate shift. In the case of the model misspecification we show that the performance of the W-KRR under covariate shift could be substantially increased by designing an alternative reweighting function. The distinction between misspecified and wellspecified scenarios does not seem to be crucial in the learning problems under target shift.