Contextual Continuum Bandits: Static Versus Dynamic Regret

We study the contextual continuum bandits problem, where the learner sequentially receives a side information vector and has to choose an action in a convex set, minimizing a function associated to the context. The goal is to minimize all the underlying functions for the received contexts, leading to a dynamic (contextual) notion of regret, which is stronger than the standard static regret. Assuming that the objective functions are H\"older with respect to the contexts, we demonstrate that any algorithm achieving a sub-linear static regret can be extended to achieve a sub-linear dynamic regret. We further study the case of strongly convex and smooth functions when the observations are noisy. Inspired by the interior point method and employing self-concordant barriers, we propose an algorithm achieving a sub-linear dynamic regret. Lastly, we present a minimax lower bound, implying two key facts. First, no algorithm can achieve sub-linear dynamic regret over functions that are not continuous with respect to the context. Second, for strongly convex and smooth functions, the algorithm that we propose achieves, up to a logarithmic factor, the minimax optimal rate of dynamic regret as a function of the number of queries.

Gradient-free optimization of highly smooth functions: improved analysis and a new algorithm

This work studies minimization problems with zero-order noisy oracle information under the assumption that the objective function is highly smooth and possibly satisfies additional properties. We consider two kinds of zero-order projected gradient descent algorithms, which differ in the form of the gradient estimator. The first algorithm uses a gradient estimator based on randomization over the $\ell_2$ sphere due to Bach and Perchet (2016). We present an improved analysis of this algorithm on the class of highly smooth and strongly convex functions studied in the prior work, and we derive rates of convergence for two more general classes of non-convex functions. Namely, we consider highly smooth functions satisfying the Polyak-{\L}ojasiewicz condition and the class of highly smooth functions with no additional property. The second algorithm is based on randomization over the $\ell_1$ sphere, and it extends to the highly smooth setting the algorithm that was recently proposed for Lipschitz convex functions in Akhavan et al. (2022). We show that, in the case of noiseless oracle, this novel algorithm enjoys better bounds on bias and variance than the $\ell_2$ randomization and the commonly used Gaussian randomization algorithms, while in the noisy case both $\ell_1$ and $\ell_2$ algorithms benefit from similar improved theoretical guarantees. The improvements are achieved thanks to a new proof techniques based on Poincar\'e type inequalities for uniform distributions on the $\ell_1$ or $\ell_2$ spheres. The results are established under weak (almost adversarial) assumptions on the noise. Moreover, we provide minimax lower bounds proving optimality or near optimality of the obtained upper bounds in several cases.

Estimating the minimizer and the minimum value of a regression function under passive design

We propose a new method for estimating the minimizer $\boldsymbol{x}^*$ and the minimum value $f^*$ of a smooth and strongly convex regression function $f$ from the observations contaminated by random noise. Our estimator $\boldsymbol{z}_n$ of the minimizer $\boldsymbol{x}^*$ is based on a version of the projected gradient descent with the gradient estimated by a regularized local polynomial algorithm. Next, we propose a two-stage procedure for estimation of the minimum value $f^*$ of regression function $f$. At the first stage, we construct an accurate enough estimator of $\boldsymbol{x}^*$, which can be, for example, $\boldsymbol{z}_n$. At the second stage, we estimate the function value at the point obtained in the first stage using a rate optimal nonparametric procedure. We derive non-asymptotic upper bounds for the quadratic risk and optimization error of $\boldsymbol{z}_n$, and for the risk of estimating $f^*$. We establish minimax lower bounds showing that, under certain choice of parameters, the proposed algorithms achieve the minimax optimal rates of convergence on the class of smooth and strongly convex functions.

Benign overfitting and adaptive nonparametric regression

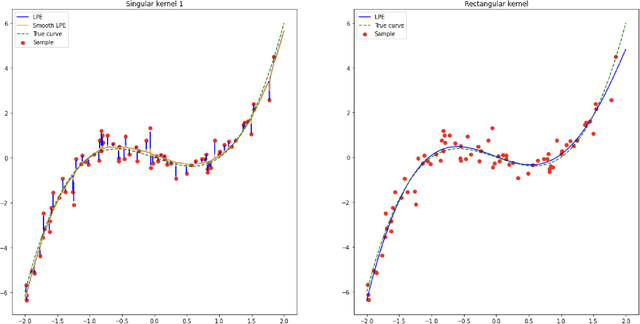
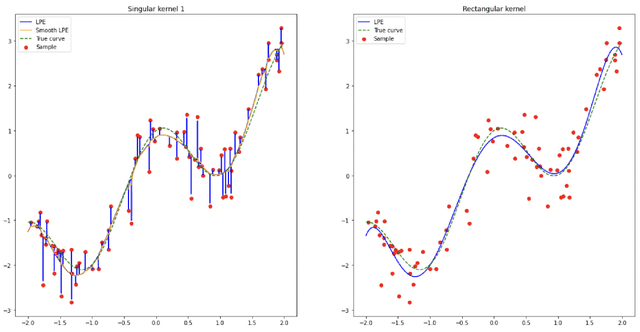
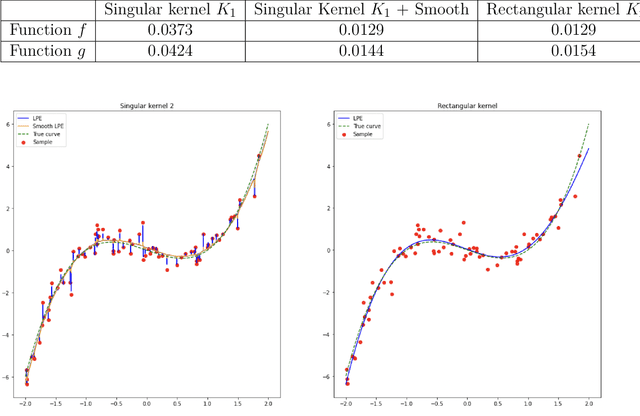
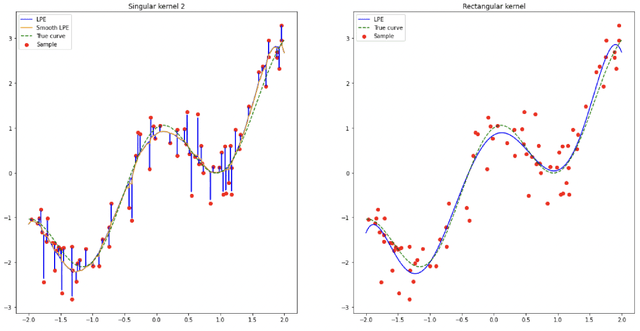
In the nonparametric regression setting, we construct an estimator which is a continuous function interpolating the data points with high probability, while attaining minimax optimal rates under mean squared risk on the scale of H\"older classes adaptively to the unknown smoothness.

A gradient estimator via L1-randomization for online zero-order optimization with two point feedback

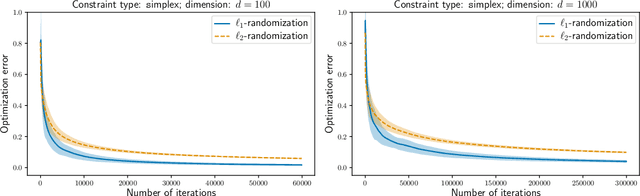
This work studies online zero-order optimization of convex and Lipschitz functions. We present a novel gradient estimator based on two function evaluation and randomization on the $\ell_1$-sphere. Considering different geometries of feasible sets and Lipschitz assumptions we analyse online mirror descent algorithm with our estimator in place of the usual gradient. We consider two types of assumptions on the noise of the zero-order oracle: canceling noise and adversarial noise. We provide an anytime and completely data-driven algorithm, which is adaptive to all parameters of the problem. In the case of canceling noise that was previously studied in the literature, our guarantees are either comparable or better than state-of-the-art bounds obtained by~\citet{duchi2015} and \citet{Shamir17} for non-adaptive algorithms. Our analysis is based on deriving a new Poincar\'e type inequality for the uniform measure on the $\ell_1$-sphere with explicit constants, which may be of independent interest.

Exploiting Higher Order Smoothness in Derivative-free Optimization and Continuous Bandits

We study the problem of zero-order optimization of a strongly convex function. The goal is to find the minimizer of the function by a sequential exploration of its values, under measurement noise. We study the impact of higher order smoothness properties of the function on the optimization error and on the cumulative regret. To solve this problem we consider a randomized approximation of the projected gradient descent algorithm. The gradient is estimated by a randomized procedure involving two function evaluations and a smoothing kernel. We derive upper bounds for this algorithm both in the constrained and unconstrained settings and prove minimax lower bounds for any sequential search method. Our results imply that the zero-order algorithm is nearly optimal in terms of sample complexity and the problem parameters. Based on this algorithm, we also propose an estimator of the minimum value of the function achieving almost sharp oracle behavior. We compare our results with the state-of-the-art, highlighting a number of key improvements.

Does data interpolation contradict statistical optimality?

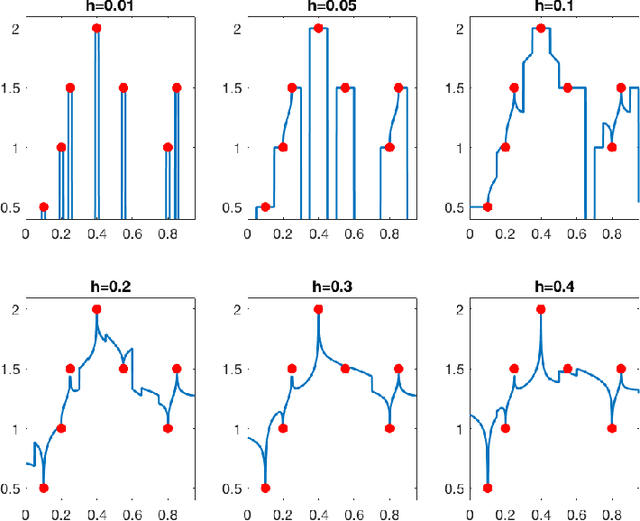
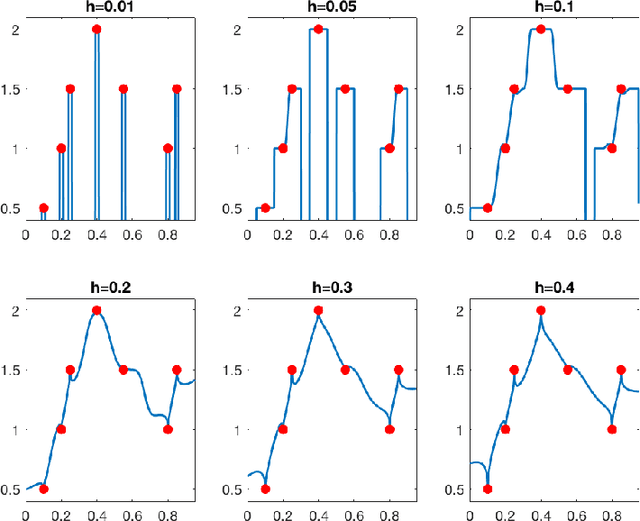
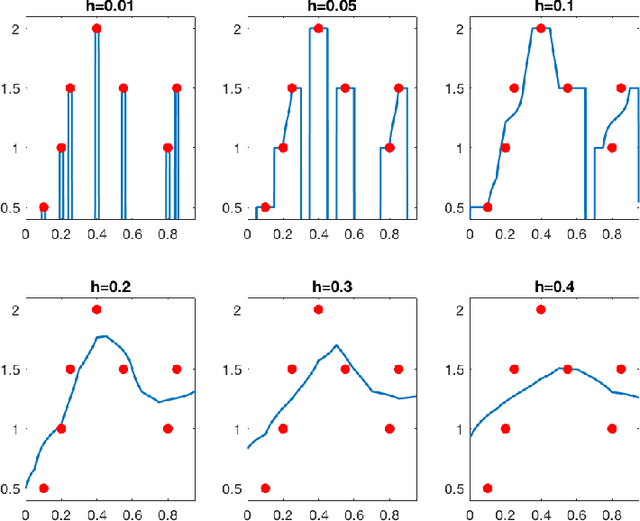
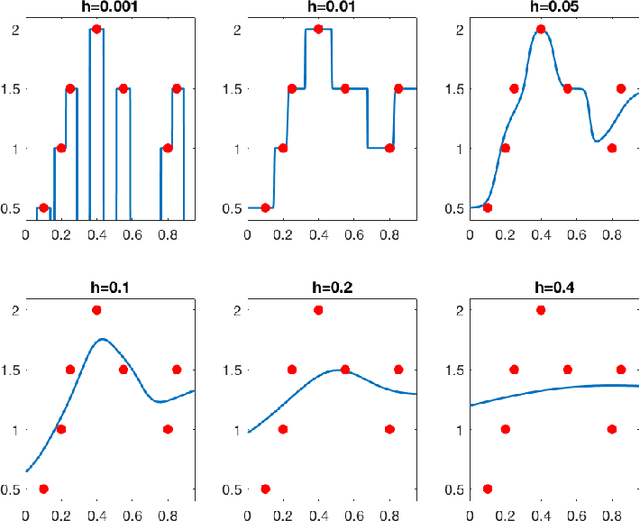
We show that learning methods interpolating the training data can achieve optimal rates for the problems of nonparametric regression and prediction with square loss.

Empirical entropy, minimax regret and minimax risk

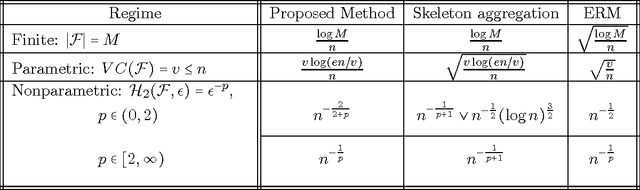
We consider the random design regression model with square loss. We propose a method that aggregates empirical minimizers (ERM) over appropriately chosen random subsets and reduces to ERM in the extreme case, and we establish sharp oracle inequalities for its risk. We show that, under the $\varepsilon^{-p}$ growth of the empirical $\varepsilon$-entropy, the excess risk of the proposed method attains the rate $n^{-2/(2+p)}$ for $p\in(0,2)$ and $n^{-1/p}$ for $p>2$ where $n$ is the sample size. Furthermore, for $p\in(0,2)$, the excess risk rate matches the behavior of the minimax risk of function estimation in regression problems under the well-specified model. This yields a conclusion that the rates of statistical estimation in well-specified models (minimax risk) and in misspecified models (minimax regret) are equivalent in the regime $p\in(0,2)$. In other words, for $p\in(0,2)$ the problem of statistical learning enjoys the same minimax rate as the problem of statistical estimation. On the contrary, for $p>2$ we show that the rates of the minimax regret are, in general, slower than for the minimax risk. Our oracle inequalities also imply the $v\log(n/v)/n$ rates for Vapnik-Chervonenkis type classes of dimension $v$ without the usual convexity assumption on the class; we show that these rates are optimal. Finally, for a slightly modified method, we derive a bound on the excess risk of $s$-sparse convex aggregation improving that of Lounici [Math. Methods Statist. 16 (2007) 246-259] and providing the optimal rate.

Nuclear norm penalization and optimal rates for noisy low rank matrix completion

This paper deals with the trace regression model where $n$ entries or linear combinations of entries of an unknown $m_1\times m_2$ matrix $A_0$ corrupted by noise are observed. We propose a new nuclear norm penalized estimator of $A_0$ and establish a general sharp oracle inequality for this estimator for arbitrary values of $n,m_1,m_2$ under the condition of isometry in expectation. Then this method is applied to the matrix completion problem. In this case, the estimator admits a simple explicit form and we prove that it satisfies oracle inequalities with faster rates of convergence than in the previous works. They are valid, in particular, in the high-dimensional setting $m_1m_2\gg n$. We show that the obtained rates are optimal up to logarithmic factors in a minimax sense and also derive, for any fixed matrix $A_0$, a non-minimax lower bound on the rate of convergence of our estimator, which coincides with the upper bound up to a constant factor. Finally, we show that our procedure provides an exact recovery of the rank of $A_0$ with probability close to 1. We also discuss the statistical learning setting where there is no underlying model determined by $A_0$ and the aim is to find the best trace regression model approximating the data.

An $\{l_1,l_2,l_{\infty}\}$-Regularization Approach to High-Dimensional Errors-in-variables Models

Several new estimation methods have been recently proposed for the linear regression model with observation error in the design. Different assumptions on the data generating process have motivated different estimators and analysis. In particular, the literature considered (1) observation errors in the design uniformly bounded by some $\bar \delta$, and (2) zero mean independent observation errors. Under the first assumption, the rates of convergence of the proposed estimators depend explicitly on $\bar \delta$, while the second assumption has been applied when an estimator for the second moment of the observational error is available. This work proposes and studies two new estimators which, compared to other procedures for regression models with errors in the design, exploit an additional $l_{\infty}$-norm regularization. The first estimator is applicable when both (1) and (2) hold but does not require an estimator for the second moment of the observational error. The second estimator is applicable under (2) and requires an estimator for the second moment of the observation error. Importantly, we impose no assumption on the accuracy of this pilot estimator, in contrast to the previously known procedures. As the recent proposals, we allow the number of covariates to be much larger than the sample size. We establish the rates of convergence of the estimators and compare them with the bounds obtained for related estimators in the literature. These comparisons show interesting insights on the interplay of the assumptions and the achievable rates of convergence.