kooplearn: A Scikit-Learn Compatible Library of Algorithms for Evolution Operator Learning

kooplearn is a machine-learning library that implements linear, kernel, and deep-learning estimators of dynamical operators and their spectral decompositions. kooplearn can model both discrete-time evolution operators (Koopman/Transfer) and continuous-time infinitesimal generators. By learning these operators, users can analyze dynamical systems via spectral methods, derive data-driven reduced-order models, and forecast future states and observables. kooplearn's interface is compliant with the scikit-learn API, facilitating its integration into existing machine learning and data science workflows. Additionally, kooplearn includes curated benchmark datasets to support experimentation, reproducibility, and the fair comparison of learning algorithms. The software is available at https://github.com/Machine-Learning-Dynamical-Systems/kooplearn.

Toward Scalable and Valid Conditional Independence Testing with Spectral Representations

Conditional independence (CI) is central to causal inference, feature selection, and graphical modeling, yet it is untestable in many settings without additional assumptions. Existing CI tests often rely on restrictive structural conditions, limiting their validity on real-world data. Kernel methods using the partial covariance operator offer a more principled approach but suffer from limited adaptivity, slow convergence, and poor scalability. In this work, we explore whether representation learning can help address these limitations. Specifically, we focus on representations derived from the singular value decomposition of the partial covariance operator and use them to construct a simple test statistic, reminiscent of the Hilbert-Schmidt Independence Criterion (HSIC). We also introduce a practical bi-level contrastive algorithm to learn these representations. Our theory links representation learning error to test performance and establishes asymptotic validity and power guarantees. Preliminary experiments suggest that this approach offers a practical and statistically grounded path toward scalable CI testing, bridging kernel-based theory with modern representation learning.

An Empirical Bernstein Inequality for Dependent Data in Hilbert Spaces and Applications

Learning from non-independent and non-identically distributed data poses a persistent challenge in statistical learning. In this study, we introduce data-dependent Bernstein inequalities tailored for vector-valued processes in Hilbert space. Our inequalities apply to both stationary and non-stationary processes and exploit the potential rapid decay of correlations between temporally separated variables to improve estimation. We demonstrate the utility of these bounds by applying them to covariance operator estimation in the Hilbert-Schmidt norm and to operator learning in dynamical systems, achieving novel risk bounds. Finally, we perform numerical experiments to illustrate the practical implications of these bounds in both contexts.

Self-Supervised Evolution Operator Learning for High-Dimensional Dynamical Systems

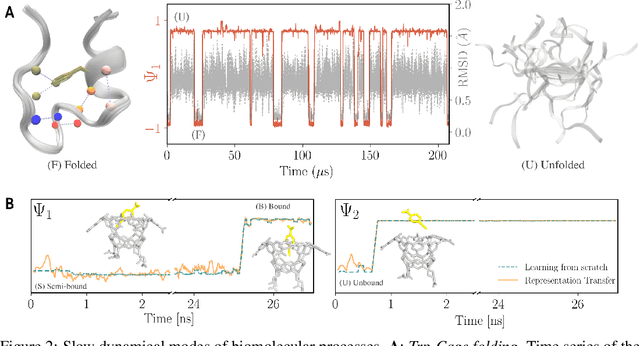
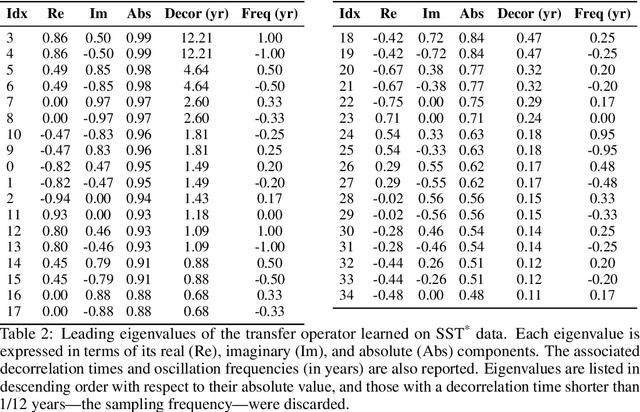
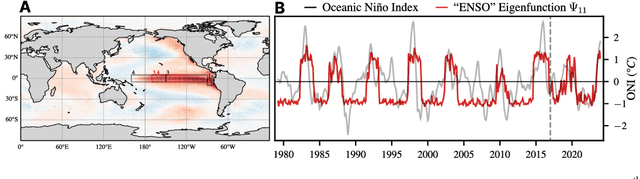
We introduce an encoder-only approach to learn the evolution operators of large-scale non-linear dynamical systems, such as those describing complex natural phenomena. Evolution operators are particularly well-suited for analyzing systems that exhibit complex spatio-temporal patterns and have become a key analytical tool across various scientific communities. As terabyte-scale weather datasets and simulation tools capable of running millions of molecular dynamics steps per day are becoming commodities, our approach provides an effective tool to make sense of them from a data-driven perspective. The core of it lies in a remarkable connection between self-supervised representation learning methods and the recently established learning theory of evolution operators. To show the usefulness of the proposed method, we test it across multiple scientific domains: explaining the folding dynamics of small proteins, the binding process of drug-like molecules in host sites, and autonomously finding patterns in climate data. Code and data to reproduce the experiments are made available open source.

QuantFormer: Learning to Quantize for Neural Activity Forecasting in Mouse Visual Cortex

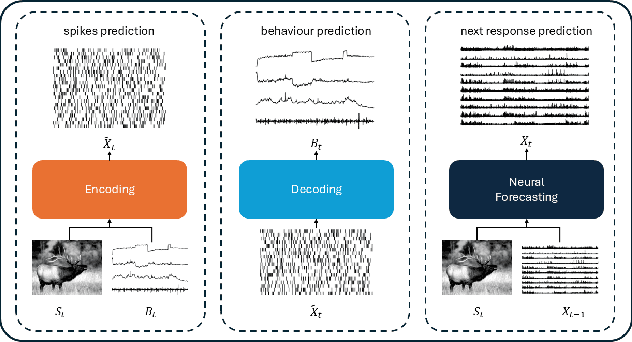
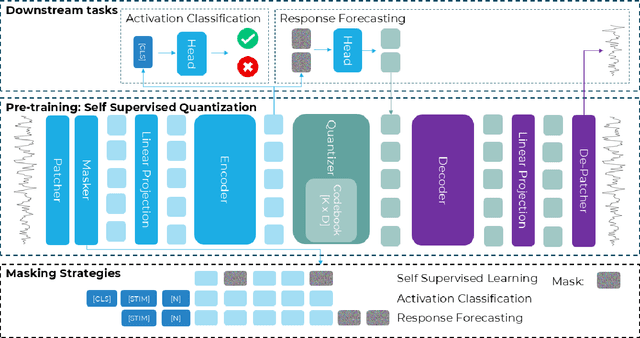
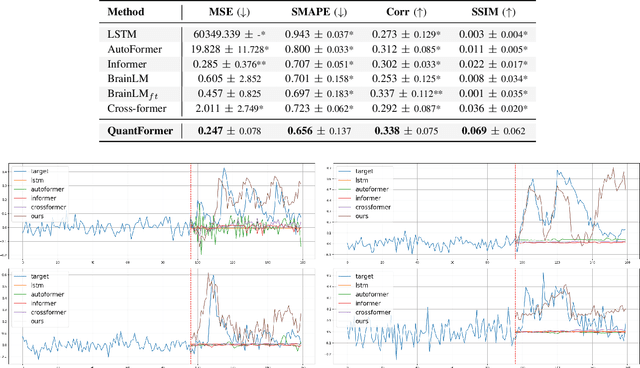
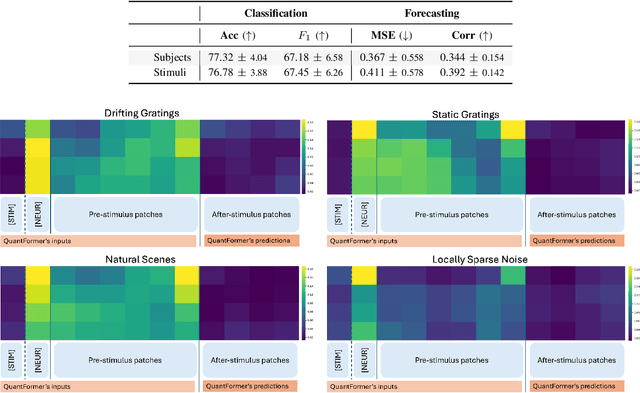
Understanding complex animal behaviors hinges on deciphering the neural activity patterns within brain circuits, making the ability to forecast neural activity crucial for developing predictive models of brain dynamics. This capability holds immense value for neuroscience, particularly in applications such as real-time optogenetic interventions. While traditional encoding and decoding methods have been used to map external variables to neural activity and vice versa, they focus on interpreting past data. In contrast, neural forecasting aims to predict future neural activity, presenting a unique and challenging task due to the spatiotemporal sparsity and complex dependencies of neural signals. Existing transformer-based forecasting methods, while effective in many domains, struggle to capture the distinctiveness of neural signals characterized by spatiotemporal sparsity and intricate dependencies. To address this challenge, we here introduce QuantFormer, a transformer-based model specifically designed for forecasting neural activity from two-photon calcium imaging data. Unlike conventional regression-based approaches, QuantFormerreframes the forecasting task as a classification problem via dynamic signal quantization, enabling more effective learning of sparse neural activation patterns. Additionally, QuantFormer tackles the challenge of analyzing multivariate signals from an arbitrary number of neurons by incorporating neuron-specific tokens, allowing scalability across diverse neuronal populations. Trained with unsupervised quantization on the Allen dataset, QuantFormer sets a new benchmark in forecasting mouse visual cortex activity. It demonstrates robust performance and generalization across various stimuli and individuals, paving the way for a foundational model in neural signal prediction.

Unlocking State-Tracking in Linear RNNs Through Negative Eigenvalues

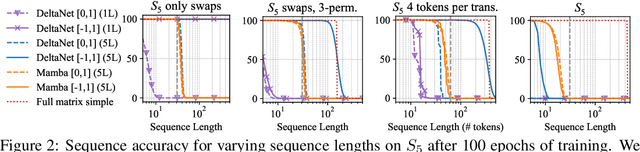
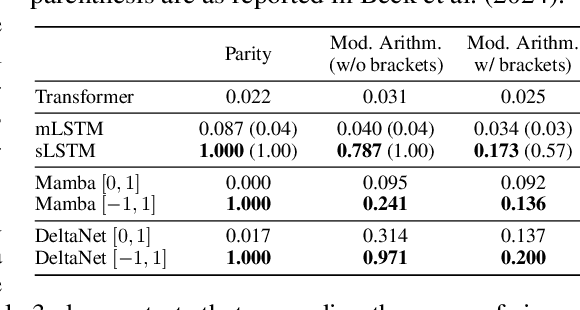
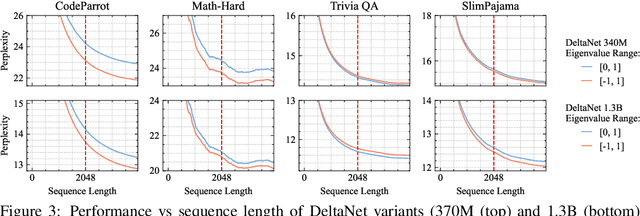
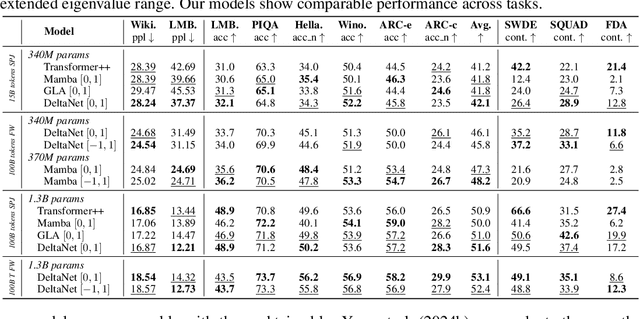
Linear Recurrent Neural Networks (LRNNs) such as Mamba, RWKV, GLA, mLSTM, and DeltaNet have emerged as efficient alternatives to Transformers in large language modeling, offering linear scaling with sequence length and improved training efficiency. However, LRNNs struggle to perform state-tracking which may impair performance in tasks such as code evaluation or tracking a chess game. Even parity, the simplest state-tracking task, which non-linear RNNs like LSTM handle effectively, cannot be solved by current LRNNs. Recently, Sarrof et al. (2024) demonstrated that the failure of LRNNs like Mamba to solve parity stems from restricting the value range of their diagonal state-transition matrices to $[0, 1]$ and that incorporating negative values can resolve this issue. We extend this result to non-diagonal LRNNs, which have recently shown promise in models such as DeltaNet. We prove that finite precision LRNNs with state-transition matrices having only positive eigenvalues cannot solve parity, while complex eigenvalues are needed to count modulo $3$. Notably, we also prove that LRNNs can learn any regular language when their state-transition matrices are products of identity minus vector outer product matrices, each with eigenvalues in the range $[-1, 1]$. Our empirical results confirm that extending the eigenvalue range of models like Mamba and DeltaNet to include negative values not only enables them to solve parity but consistently improves their performance on state-tracking tasks. Furthermore, pre-training LRNNs with an extended eigenvalue range for language modeling achieves comparable performance and stability while showing promise on code and math data. Our work enhances the expressivity of modern LRNNs, broadening their applicability without changing the cost of training or inference.

Hyperparameter Optimization in Machine Learning

Hyperparameters are configuration variables controlling the behavior of machine learning algorithms. They are ubiquitous in machine learning and artificial intelligence and the choice of their values determine the effectiveness of systems based on these technologies. Manual hyperparameter search is often unsatisfactory and becomes unfeasible when the number of hyperparameters is large. Automating the search is an important step towards automating machine learning, freeing researchers and practitioners alike from the burden of finding a good set of hyperparameters by trial and error. In this survey, we present a unified treatment of hyperparameter optimization, providing the reader with examples and insights into the state-of-the-art. We cover the main families of techniques to automate hyperparameter search, often referred to as hyperparameter optimization or tuning, including random and quasi-random search, bandit-, model- and gradient- based approaches. We further discuss extensions, including online, constrained, and multi-objective formulations, touch upon connections with other fields such as meta-learning and neural architecture search, and conclude with open questions and future research directions.

Laplace Transform Based Low-Complexity Learning of Continuous Markov Semigroups

Markov processes serve as a universal model for many real-world random processes. This paper presents a data-driven approach for learning these models through the spectral decomposition of the infinitesimal generator (IG) of the Markov semigroup. The unbounded nature of IGs complicates traditional methods such as vector-valued regression and Hilbert-Schmidt operator analysis. Existing techniques, including physics-informed kernel regression, are computationally expensive and limited in scope, with no recovery guarantees for transfer operator methods when the time-lag is small. We propose a novel method that leverages the IG's resolvent, characterized by the Laplace transform of transfer operators. This approach is robust to time-lag variations, ensuring accurate eigenvalue learning even for small time-lags. Our statistical analysis applies to a broader class of Markov processes than current methods while reducing computational complexity from quadratic to linear in the state dimension. Finally, we illustrate the behaviour of our method in two experiments.

Adaptive AI-Driven Material Synthesis: Towards Autonomous 2D Materials Growth

Two-dimensional (2D) materials are poised to revolutionize current solid-state technology with their extraordinary properties. Yet, the primary challenge remains their scalable production. While there have been significant advancements, much of the scientific progress has depended on the exfoliation of materials, a method that poses severe challenges for large-scale applications. With the advent of artificial intelligence (AI) in materials science, innovative synthesis methodologies are now on the horizon. This study explores the forefront of autonomous materials synthesis using an artificial neural network (ANN) trained by evolutionary methods, focusing on the efficient production of graphene. Our approach demonstrates that a neural network can iteratively and autonomously learn a time-dependent protocol for the efficient growth of graphene, without requiring pretraining on what constitutes an effective recipe. Evaluation criteria are based on the proximity of the Raman signature to that of monolayer graphene: higher scores are granted to outcomes whose spectrum more closely resembles that of an ideal continuous monolayer structure. This feedback mechanism allows for iterative refinement of the ANN's time-dependent synthesis protocols, progressively improving sample quality. Through the advancement and application of AI methodologies, this work makes a substantial contribution to the field of materials engineering, fostering a new era of innovation and efficiency in the synthesis process.

Neural Conditional Probability for Inference

We introduce NCP (Neural Conditional Probability), a novel operator-theoretic approach for learning conditional distributions with a particular focus on inference tasks. NCP can be used to build conditional confidence regions and extract important statistics like conditional quantiles, mean, and covariance. It offers streamlined learning through a single unconditional training phase, facilitating efficient inference without the need for retraining even when conditioning changes. By tapping into the powerful approximation capabilities of neural networks, our method efficiently handles a wide variety of complex probability distributions, effectively dealing with nonlinear relationships between input and output variables. Theoretical guarantees ensure both optimization consistency and statistical accuracy of the NCP method. Our experiments show that our approach matches or beats leading methods using a simple Multi-Layer Perceptron (MLP) with two hidden layers and GELU activations. This demonstrates that a minimalistic architecture with a theoretically grounded loss function can achieve competitive results without sacrificing performance, even in the face of more complex architectures.