Unlocking State-Tracking in Linear RNNs Through Negative Eigenvalues

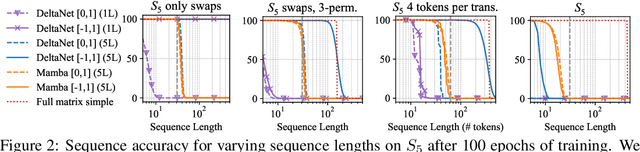
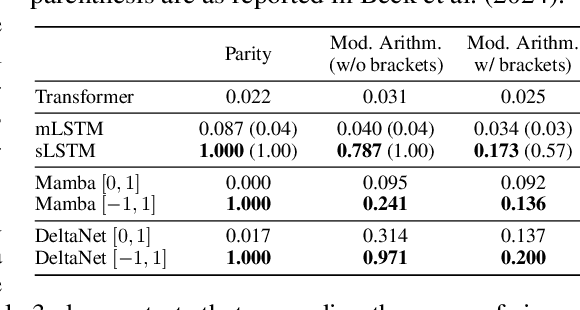
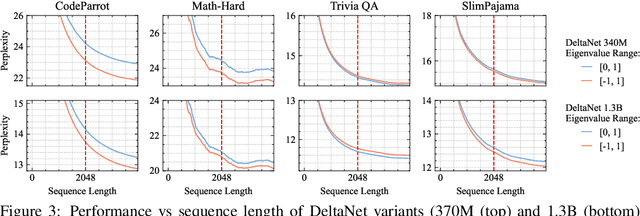
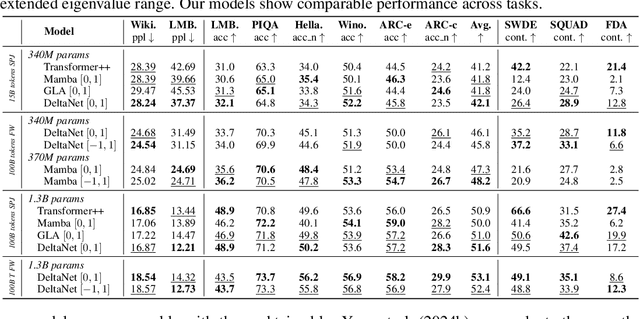
Linear Recurrent Neural Networks (LRNNs) such as Mamba, RWKV, GLA, mLSTM, and DeltaNet have emerged as efficient alternatives to Transformers in large language modeling, offering linear scaling with sequence length and improved training efficiency. However, LRNNs struggle to perform state-tracking which may impair performance in tasks such as code evaluation or tracking a chess game. Even parity, the simplest state-tracking task, which non-linear RNNs like LSTM handle effectively, cannot be solved by current LRNNs. Recently, Sarrof et al. (2024) demonstrated that the failure of LRNNs like Mamba to solve parity stems from restricting the value range of their diagonal state-transition matrices to $[0, 1]$ and that incorporating negative values can resolve this issue. We extend this result to non-diagonal LRNNs, which have recently shown promise in models such as DeltaNet. We prove that finite precision LRNNs with state-transition matrices having only positive eigenvalues cannot solve parity, while complex eigenvalues are needed to count modulo $3$. Notably, we also prove that LRNNs can learn any regular language when their state-transition matrices are products of identity minus vector outer product matrices, each with eigenvalues in the range $[-1, 1]$. Our empirical results confirm that extending the eigenvalue range of models like Mamba and DeltaNet to include negative values not only enables them to solve parity but consistently improves their performance on state-tracking tasks. Furthermore, pre-training LRNNs with an extended eigenvalue range for language modeling achieves comparable performance and stability while showing promise on code and math data. Our work enhances the expressivity of modern LRNNs, broadening their applicability without changing the cost of training or inference.

Nonsmooth Implicit Differentiation: Deterministic and Stochastic Convergence Rates

We study the problem of efficiently computing the derivative of the fixed-point of a parametric nondifferentiable contraction map. This problem has wide applications in machine learning, including hyperparameter optimization, meta-learning and data poisoning attacks. We analyze two popular approaches: iterative differentiation (ITD) and approximate implicit differentiation (AID). A key challenge behind the nonsmooth setting is that the chain rule does not hold anymore. Building upon the recent work by Bolte et al. (2022), who proved linear convergence of nondifferentiable ITD, we provide an improved linear rate for ITD and a slightly better rate for AID, both in the deterministic case. We further introduce NSID, a new stochastic method to compute the implicit derivative when the fixed point is defined as the composition of an outer map and an inner map which is accessible only through a stochastic unbiased estimator. We establish rates for the convergence of NSID, encompassing the best available rates in the smooth setting. We present illustrative experiments confirming our analysis.

Is Mamba Capable of In-Context Learning?

This work provides empirical evidence that Mamba, a newly proposed selective structured state space model, has similar in-context learning (ICL) capabilities as transformers. We evaluated Mamba on tasks involving simple function approximation as well as more complex natural language processing problems. Our results demonstrate that across both categories of tasks, Mamba matches the performance of transformer models for ICL. Further analysis reveals that like transformers, Mamba appears to solve ICL problems by incrementally optimizing its internal representations. Overall, our work suggests that Mamba can be an efficient alternative to transformers for ICL tasks involving longer input sequences.

Deep projection networks for learning time-homogeneous dynamical systems

We consider the general class of time-homogeneous dynamical systems, both discrete and continuous, and study the problem of learning a meaningful representation of the state from observed data. This is instrumental for the task of learning a forward transfer operator of the system, that in turn can be used for forecasting future states or observables. The representation, typically parametrized via a neural network, is associated with a projection operator and is learned by optimizing an objective function akin to that of canonical correlation analysis (CCA). However, unlike CCA, our objective avoids matrix inversions and therefore is generally more stable and applicable to challenging scenarios. Our objective is a tight relaxation of CCA and we further enhance it by proposing two regularization schemes, one encouraging the orthogonality of the components of the representation while the other exploiting Chapman-Kolmogorov's equation. We apply our method to challenging discrete dynamical systems, discussing improvements over previous methods, as well as to continuous dynamical systems.

Group Meritocratic Fairness in Linear Contextual Bandits

We study the linear contextual bandit problem where an agent has to select one candidate from a pool and each candidate belongs to a sensitive group. In this setting, candidates' rewards may not be directly comparable between groups, for example when the agent is an employer hiring candidates from different ethnic groups and some groups have a lower reward due to discriminatory bias and/or social injustice. We propose a notion of fairness that states that the agent's policy is fair when it selects a candidate with highest relative rank, which measures how good the reward is when compared to candidates from the same group. This is a very strong notion of fairness, since the relative rank is not directly observed by the agent and depends on the underlying reward model and on the distribution of rewards. Thus we study the problem of learning a policy which approximates a fair policy under the condition that the contexts are independent between groups and the distribution of rewards of each group is absolutely continuous. In particular, we design a greedy policy which at each round constructs a ridge regression estimator from the observed context-reward pairs, and then computes an estimate of the relative rank of each candidate using the empirical cumulative distribution function. We prove that the greedy policy achieves, after $T$ rounds, up to log factors and with high probability, a fair pseudo-regret of order $\sqrt{dT}$, where $d$ is the dimension of the context vectors. The policy also satisfies demographic parity at each round when averaged over all possible information available before the selection. We finally show with a proof of concept simulation that our policy achieves sub-linear fair pseudo-regret also in practice.

Bilevel Optimization with a Lower-level Contraction: Optimal Sample Complexity without Warm-Start

We analyze a general class of bilevel problems, in which the upper-level problem consists in the minimization of a smooth objective function and the lower-level problem is to find the fixed point of a smooth contraction map. This type of problems include instances of meta-learning, hyperparameter optimization and data poisoning adversarial attacks. Several recent works have proposed algorithms which warm-start the lower-level problem, i.e. they use the previous lower-level approximate solution as a staring point for the lower-level solver. This warm-start procedure allows one to improve the sample complexity in both the stochastic and deterministic settings, achieving in some cases the order-wise optimal sample complexity. We show that without warm-start, it is still possible to achieve order-wise optimal and near-optimal sample complexity for the stochastic and deterministic settings, respectively. In particular, we propose a simple method which uses stochastic fixed point iterations at the lower-level and projected inexact gradient descent at the upper-level, that reaches an $\epsilon$-stationary point using $O(\epsilon^{-2})$ and $\tilde{O}(\epsilon^{-1})$ samples for the stochastic and the deterministic setting, respectively. Compared to methods using warm-start, ours is better suited for meta-learning and yields a simpler analysis that does not need to study the coupled interactions between the upper-level and lower-level iterates.

Meta-Forecasting by combining Global Deep Representations with Local Adaptation

While classical time series forecasting considers individual time series in isolation, recent advances based on deep learning showed that jointly learning from a large pool of related time series can boost the forecasting accuracy. However, the accuracy of these methods suffers greatly when modeling out-of-sample time series, significantly limiting their applicability compared to classical forecasting methods. To bridge this gap, we adopt a meta-learning view of the time series forecasting problem. We introduce a novel forecasting method, called Meta Global-Local Auto-Regression (Meta-GLAR), that adapts to each time series by learning in closed-form the mapping from the representations produced by a recurrent neural network (RNN) to one-step-ahead forecasts. Crucially, the parameters ofthe RNN are learned across multiple time series by backpropagating through the closed-form adaptation mechanism. In our extensive empirical evaluation we show that our method is competitive with the state-of-the-art in out-of-sample forecasting accuracy reported in earlier work.

Convergence Properties of Stochastic Hypergradients

Bilevel optimization problems are receiving increasing attention in machine learning as they provide a natural framework for hyperparameter optimization and meta-learning. A key step to tackle these problems in the design of optimization algorithms for bilevel optimization is the efficient computation of the gradient of the upper-level objective (hypergradient). In this work, we study stochastic approximation schemes for the hypergradient, which are important when the lower-level problem is empirical risk minimization on a large dataset. We provide iteration complexity bounds for the mean square error of the hypergradient approximation, under the assumption that the lower-level problem is accessible only through a stochastic mapping which is a contraction in expectation. Preliminary numerical experiments support our theoretical analysis.

On the Iteration Complexity of Hypergradient Computation

We study a general class of bilevel problems, consisting in the minimization of an upper-level objective which depends on the solution to a parametric fixed-point equation. Important instances arising in machine learning include hyperparameter optimization, meta-learning, and certain graph and recurrent neural networks. Typically the gradient of the upper-level objective (hypergradient) is hard or even impossible to compute exactly, which has raised the interest in approximation methods. We investigate some popular approaches to compute the hypergradient, based on reverse mode iterative differentiation and approximate implicit differentiation. Under the hypothesis that the fixed point equation is defined by a contraction mapping, we present a unified analysis which allows for the first time to quantitatively compare these methods, providing explicit bounds for their iteration complexity. This analysis suggests a hierarchy in terms of computational efficiency among the above methods, with approximate implicit differentiation based on conjugate gradient performing best. We present an extensive experimental comparison among the methods which confirm the theoretical findings.

Learning-to-Learn Stochastic Gradient Descent with Biased Regularization

We study the problem of learning-to-learn: inferring a learning algorithm that works well on tasks sampled from an unknown distribution. As class of algorithms we consider Stochastic Gradient Descent on the true risk regularized by the square euclidean distance to a bias vector. We present an average excess risk bound for such a learning algorithm. This result quantifies the potential benefit of using a bias vector with respect to the unbiased case. We then address the problem of estimating the bias from a sequence of tasks. We propose a meta-algorithm which incrementally updates the bias, as new tasks are observed. The low space and time complexity of this approach makes it appealing in practice. We provide guarantees on the learning ability of the meta-algorithm. A key feature of our results is that, when the number of tasks grows and their variance is relatively small, our learning-to-learn approach has a significant advantage over learning each task in isolation by Stochastic Gradient Descent without a bias term. We report on numerical experiments which demonstrate the effectiveness of our approach.