Conditional Meta-Learning of Linear Representations

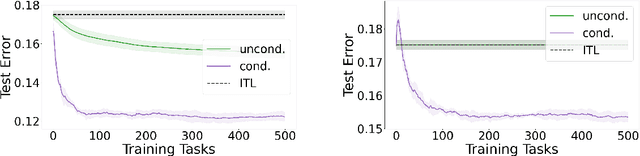
Standard meta-learning for representation learning aims to find a common representation to be shared across multiple tasks. The effectiveness of these methods is often limited when the nuances of the tasks' distribution cannot be captured by a single representation. In this work we overcome this issue by inferring a conditioning function, mapping the tasks' side information (such as the tasks' training dataset itself) into a representation tailored to the task at hand. We study environments in which our conditional strategy outperforms standard meta-learning, such as those in which tasks can be organized in separate clusters according to the representation they share. We then propose a meta-algorithm capable of leveraging this advantage in practice. In the unconditional setting, our method yields a new estimator enjoying faster learning rates and requiring less hyper-parameters to tune than current state-of-the-art methods. Our results are supported by preliminary experiments.

The Advantage of Conditional Meta-Learning for Biased Regularization and Fine-Tuning

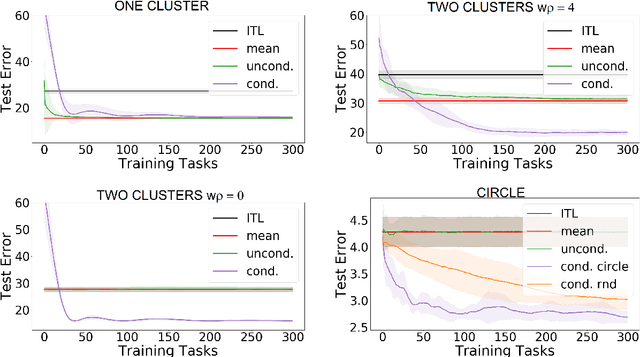
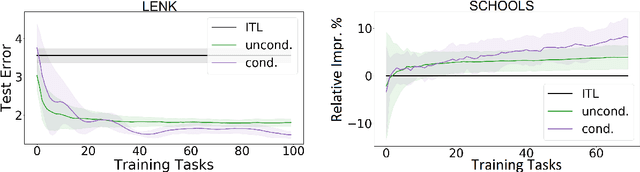
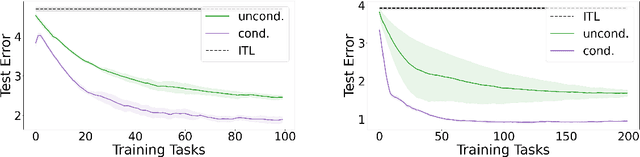
Biased regularization and fine-tuning are two recent meta-learning approaches. They have been shown to be effective to tackle distributions of tasks, in which the tasks' target vectors are all close to a common meta-parameter vector. However, these methods may perform poorly on heterogeneous environments of tasks, where the complexity of the tasks' distribution cannot be captured by a single meta-parameter vector. We address this limitation by conditional meta-learning, inferring a conditioning function mapping task's side information into a meta-parameter vector that is appropriate for that task at hand. We characterize properties of the environment under which the conditional approach brings a substantial advantage over standard meta-learning and we highlight examples of environments, such as those with multiple clusters, satisfying these properties. We then propose a convex meta-algorithm providing a comparable advantage also in practice. Numerical experiments confirm our theoretical findings.

Online Parameter-Free Learning of Multiple Low Variance Tasks

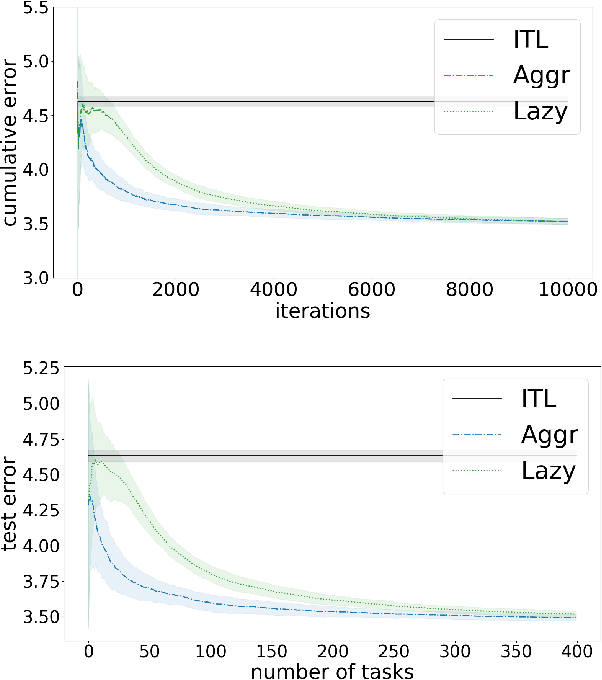
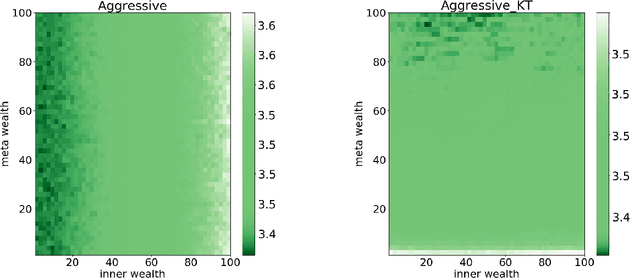
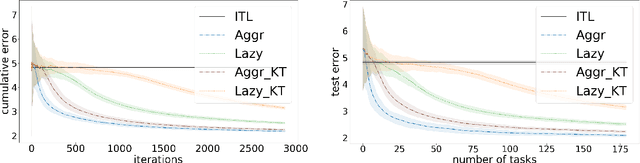
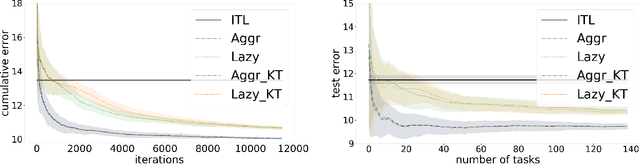
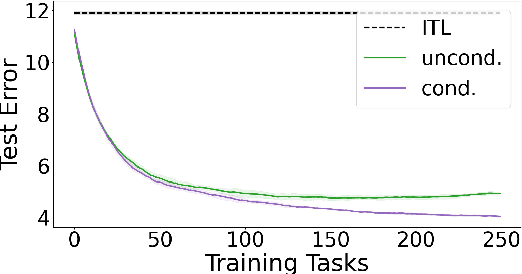
We propose a method to learn a common bias vector for a growing sequence of low-variance tasks. Unlike state-of-the-art approaches, our method does not require tuning any hyper-parameter. Our approach is presented in the non-statistical setting and can be of two variants. The "aggressive" one updates the bias after each datapoint, the "lazy" one updates the bias only at the end of each task. We derive an across-tasks regret bound for the method. When compared to state-of-the-art approaches, the aggressive variant returns faster rates, the lazy one recovers standard rates, but with no need of tuning hyper-parameters. We then adapt the methods to the statistical setting: the aggressive variant becomes a multi-task learning method, the lazy one a meta-learning method. Experiments confirm the effectiveness of our methods in practice.

Learning-to-Learn Stochastic Gradient Descent with Biased Regularization

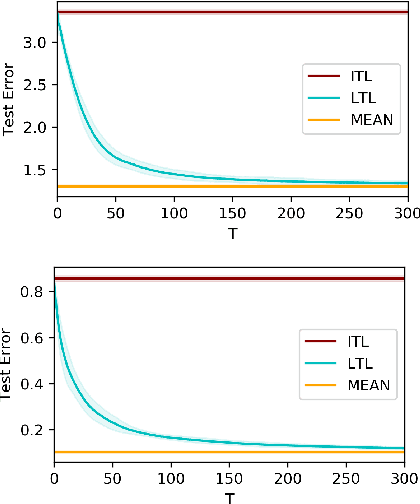
We study the problem of learning-to-learn: inferring a learning algorithm that works well on tasks sampled from an unknown distribution. As class of algorithms we consider Stochastic Gradient Descent on the true risk regularized by the square euclidean distance to a bias vector. We present an average excess risk bound for such a learning algorithm. This result quantifies the potential benefit of using a bias vector with respect to the unbiased case. We then address the problem of estimating the bias from a sequence of tasks. We propose a meta-algorithm which incrementally updates the bias, as new tasks are observed. The low space and time complexity of this approach makes it appealing in practice. We provide guarantees on the learning ability of the meta-algorithm. A key feature of our results is that, when the number of tasks grows and their variance is relatively small, our learning-to-learn approach has a significant advantage over learning each task in isolation by Stochastic Gradient Descent without a bias term. We report on numerical experiments which demonstrate the effectiveness of our approach.

Incremental Learning-to-Learn with Statistical Guarantees

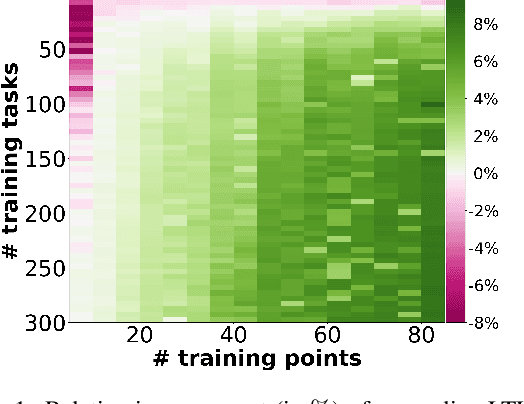
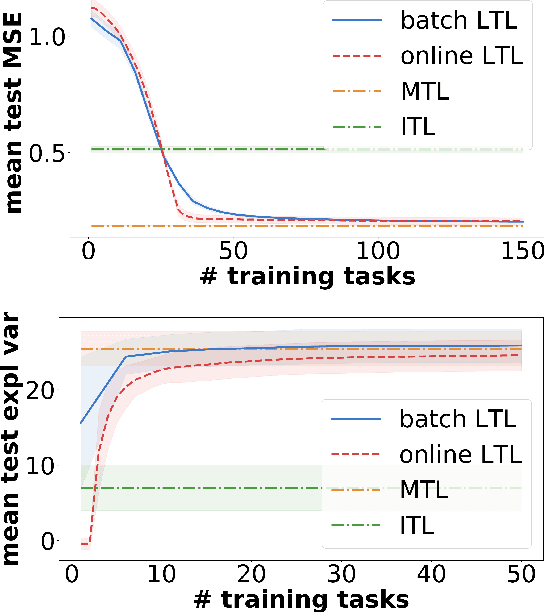
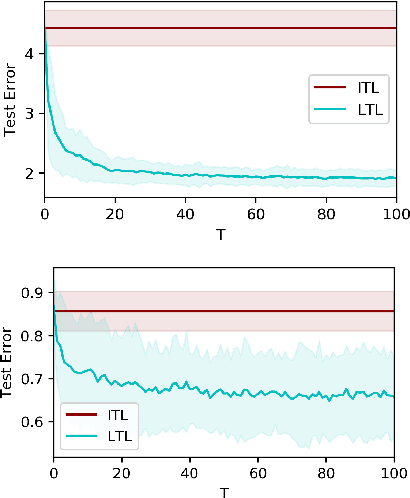
In learning-to-learn the goal is to infer a learning algorithm that works well on a class of tasks sampled from an unknown meta distribution. In contrast to previous work on batch learning-to-learn, we consider a scenario where tasks are presented sequentially and the algorithm needs to adapt incrementally to improve its performance on future tasks. Key to this setting is for the algorithm to rapidly incorporate new observations into the model as they arrive, without keeping them in memory. We focus on the case where the underlying algorithm is ridge regression parameterized by a positive semidefinite matrix. We propose to learn this matrix by applying a stochastic strategy to minimize the empirical error incurred by ridge regression on future tasks sampled from the meta distribution. We study the statistical properties of the proposed algorithm and prove non-asymptotic bounds on its excess transfer risk, that is, the generalization performance on new tasks from the same meta distribution. We compare our online learning-to-learn approach with a state of the art batch method, both theoretically and empirically.