Incremental Learning-to-Learn with Statistical Guarantees
Paper and Code
Mar 21, 2018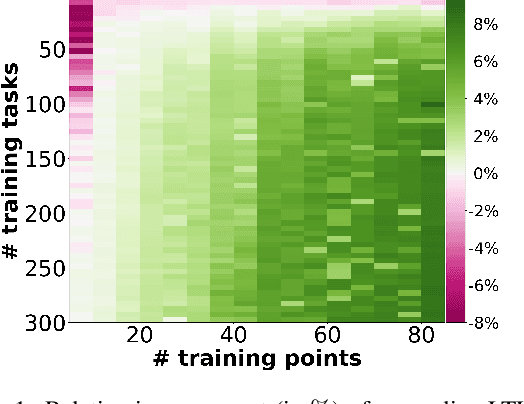

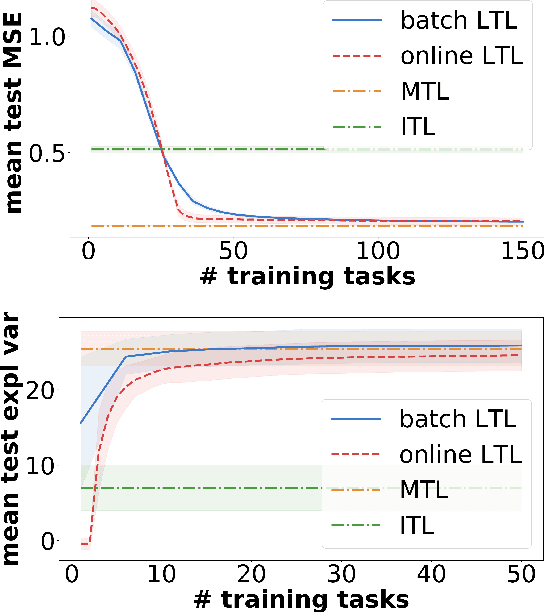
In learning-to-learn the goal is to infer a learning algorithm that works well on a class of tasks sampled from an unknown meta distribution. In contrast to previous work on batch learning-to-learn, we consider a scenario where tasks are presented sequentially and the algorithm needs to adapt incrementally to improve its performance on future tasks. Key to this setting is for the algorithm to rapidly incorporate new observations into the model as they arrive, without keeping them in memory. We focus on the case where the underlying algorithm is ridge regression parameterized by a positive semidefinite matrix. We propose to learn this matrix by applying a stochastic strategy to minimize the empirical error incurred by ridge regression on future tasks sampled from the meta distribution. We study the statistical properties of the proposed algorithm and prove non-asymptotic bounds on its excess transfer risk, that is, the generalization performance on new tasks from the same meta distribution. We compare our online learning-to-learn approach with a state of the art batch method, both theoretically and empirically.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge