Hybrid-Segmentor: A Hybrid Approach to Automated Fine-Grained Crack Segmentation in Civil Infrastructure

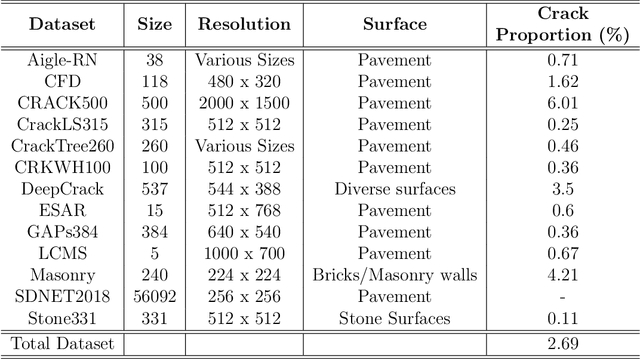
Detecting and segmenting cracks in infrastructure, such as roads and buildings, is crucial for safety and cost-effective maintenance. In spite of the potential of deep learning, there are challenges in achieving precise results and handling diverse crack types. With the proposed dataset and model, we aim to enhance crack detection and infrastructure maintenance. We introduce Hybrid-Segmentor, an encoder-decoder based approach that is capable of extracting both fine-grained local and global crack features. This allows the model to improve its generalization capabilities in distinguish various type of shapes, surfaces and sizes of cracks. To keep the computational performances low for practical purposes, while maintaining the high the generalization capabilities of the model, we incorporate a self-attention model at the encoder level, while reducing the complexity of the decoder component. The proposed model outperforms existing benchmark models across 5 quantitative metrics (accuracy 0.971, precision 0.804, recall 0.744, F1-score 0.770, and IoU score 0.630), achieving state-of-the-art status.

Operator World Models for Reinforcement Learning

Policy Mirror Descent (PMD) is a powerful and theoretically sound methodology for sequential decision-making. However, it is not directly applicable to Reinforcement Learning (RL) due to the inaccessibility of explicit action-value functions. We address this challenge by introducing a novel approach based on learning a world model of the environment using conditional mean embeddings. We then leverage the operatorial formulation of RL to express the action-value function in terms of this quantity in closed form via matrix operations. Combining these estimators with PMD leads to POWR, a new RL algorithm for which we prove convergence rates to the global optimum. Preliminary experiments in finite and infinite state settings support the effectiveness of our method.

Closed-form Filtering for Non-linear Systems

Sequential Bayesian Filtering aims to estimate the current state distribution of a Hidden Markov Model, given the past observations. The problem is well-known to be intractable for most application domains, except in notable cases such as the tabular setting or for linear dynamical systems with gaussian noise. In this work, we propose a new class of filters based on Gaussian PSD Models, which offer several advantages in terms of density approximation and computational efficiency. We show that filtering can be efficiently performed in closed form when transitions and observations are Gaussian PSD Models. When the transition and observations are approximated by Gaussian PSD Models, we show that our proposed estimator enjoys strong theoretical guarantees, with estimation error that depends on the quality of the approximation and is adaptive to the regularity of the transition probabilities. In particular, we identify regimes in which our proposed filter attains a TV $\epsilon$-error with memory and computational complexity of $O(\epsilon^{-1})$ and $O(\epsilon^{-3/2})$ respectively, including the offline learning step, in contrast to the $O(\epsilon^{-2})$ complexity of sampling methods such as particle filtering.

Robust Meta-Representation Learning via Global Label Inference and Classification

Few-shot learning (FSL) is a central problem in meta-learning, where learners must efficiently learn from few labeled examples. Within FSL, feature pre-training has recently become an increasingly popular strategy to significantly improve generalization performance. However, the contribution of pre-training is often overlooked and understudied, with limited theoretical understanding of its impact on meta-learning performance. Further, pre-training requires a consistent set of global labels shared across training tasks, which may be unavailable in practice. In this work, we address the above issues by first showing the connection between pre-training and meta-learning. We discuss why pre-training yields more robust meta-representation and connect the theoretical analysis to existing works and empirical results. Secondly, we introduce Meta Label Learning (MeLa), a novel meta-learning algorithm that learns task relations by inferring global labels across tasks. This allows us to exploit pre-training for FSL even when global labels are unavailable or ill-defined. Lastly, we introduce an augmented pre-training procedure that further improves the learned meta-representation. Empirically, MeLa outperforms existing methods across a diverse range of benchmarks, in particular under a more challenging setting where the number of training tasks is limited and labels are task-specific. We also provide extensive ablation study to highlight its key properties.

Schedule-Robust Online Continual Learning

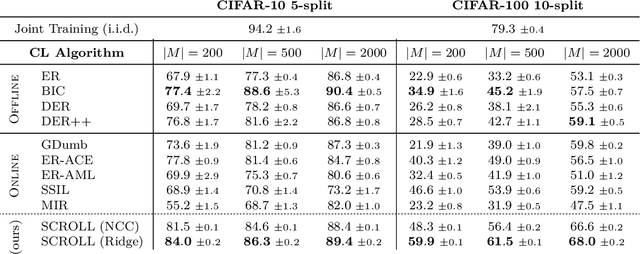
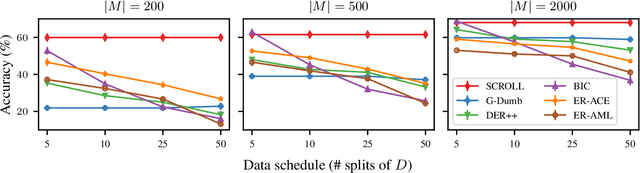
A continual learning (CL) algorithm learns from a non-stationary data stream. The non-stationarity is modeled by some schedule that determines how data is presented over time. Most current methods make strong assumptions on the schedule and have unpredictable performance when such requirements are not met. A key challenge in CL is thus to design methods robust against arbitrary schedules over the same underlying data, since in real-world scenarios schedules are often unknown and dynamic. In this work, we introduce the notion of schedule-robustness for CL and a novel approach satisfying this desirable property in the challenging online class-incremental setting. We also present a new perspective on CL, as the process of learning a schedule-robust predictor, followed by adapting the predictor using only replay data. Empirically, we demonstrate that our approach outperforms existing methods on CL benchmarks for image classification by a large margin.

Learning Dynamical Systems via Koopman Operator Regression in Reproducing Kernel Hilbert Spaces

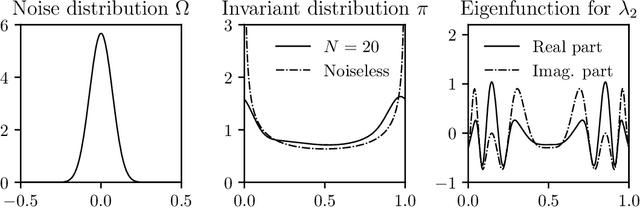
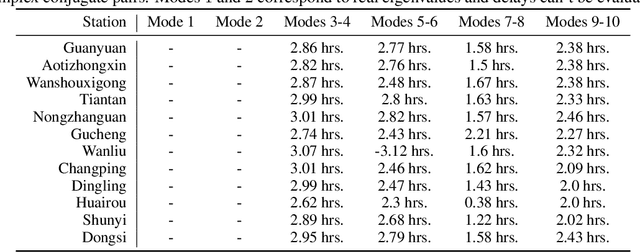
We study a class of dynamical systems modelled as Markov chains that admit an invariant distribution via the corresponding transfer, or Koopman, operator. While data-driven algorithms to reconstruct such operators are well known, their relationship with statistical learning is largely unexplored. We formalize a framework to learn the Koopman operator from finite data trajectories of the dynamical system. We consider the restriction of this operator to a reproducing kernel Hilbert space and introduce a notion of risk, from which different estimators naturally arise. We link the risk with the estimation of the spectral decomposition of the Koopman operator. These observations motivate a reduced-rank operator regression (RRR) estimator. We derive learning bounds for the proposed estimator, holding both in i.i.d. and non i.i.d. settings, the latter in terms of mixing coefficients. Our results suggest RRR might be beneficial over other widely used estimators as confirmed in numerical experiments both for forecasting and mode decomposition.

Modular Adaptive Policy Selection for Multi-Task Imitation Learning through Task Division

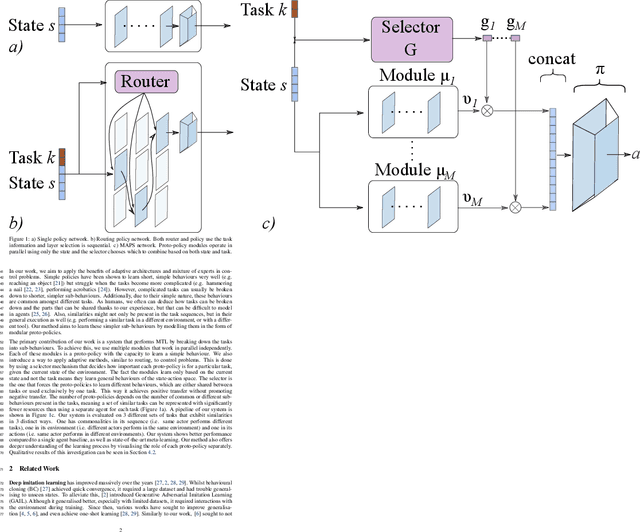
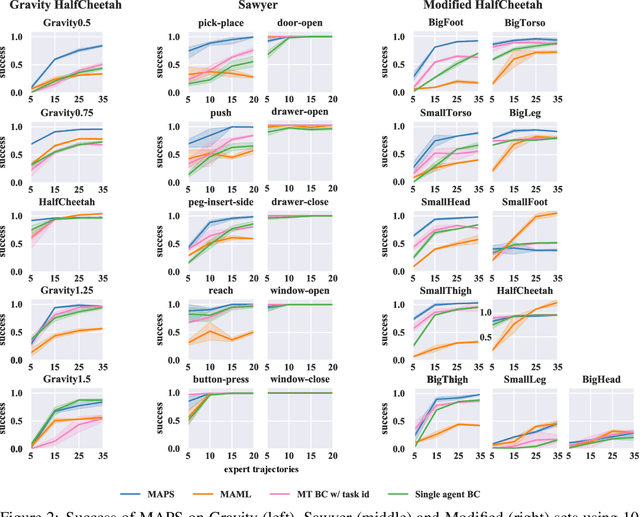
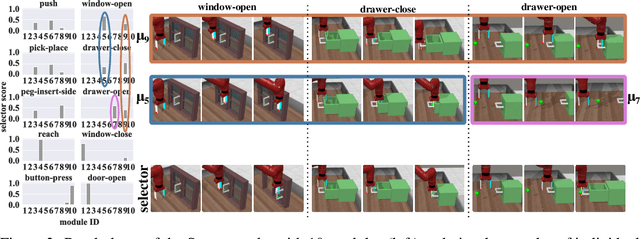
Deep imitation learning requires many expert demonstrations, which can be hard to obtain, especially when many tasks are involved. However, different tasks often share similarities, so learning them jointly can greatly benefit them and alleviate the need for many demonstrations. But, joint multi-task learning often suffers from negative transfer, sharing information that should be task-specific. In this work, we introduce a method to perform multi-task imitation while allowing for task-specific features. This is done by using proto-policies as modules to divide the tasks into simple sub-behaviours that can be shared. The proto-policies operate in parallel and are adaptively chosen by a selector mechanism that is jointly trained with the modules. Experiments on different sets of tasks show that our method improves upon the accuracy of single agents, task-conditioned and multi-headed multi-task agents, as well as state-of-the-art meta learning agents. We also demonstrate its ability to autonomously divide the tasks into both shared and task-specific sub-behaviours.

Measuring dissimilarity with diffeomorphism invariance

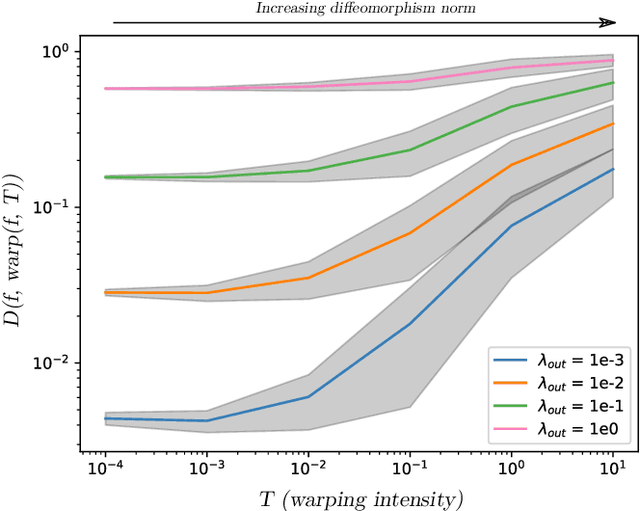
Measures of similarity (or dissimilarity) are a key ingredient to many machine learning algorithms. We introduce DID, a pairwise dissimilarity measure applicable to a wide range of data spaces, which leverages the data's internal structure to be invariant to diffeomorphisms. We prove that DID enjoys properties which make it relevant for theoretical study and practical use. By representing each datum as a function, DID is defined as the solution to an optimization problem in a Reproducing Kernel Hilbert Space and can be expressed in closed-form. In practice, it can be efficiently approximated via Nystr\"om sampling. Empirical experiments support the merits of DID.

Distribution Regression with Sliced Wasserstein Kernels

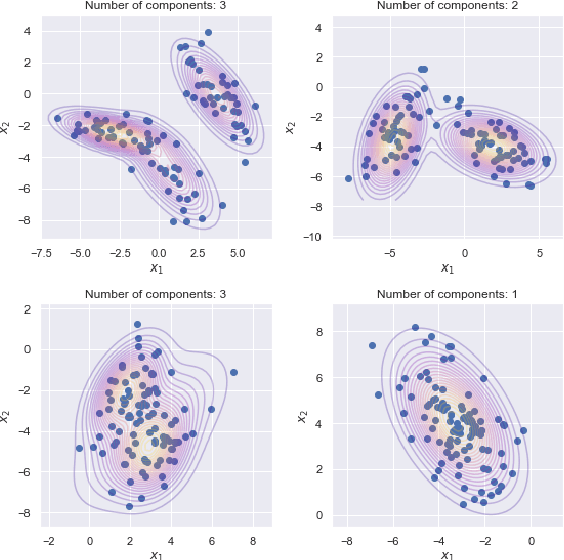
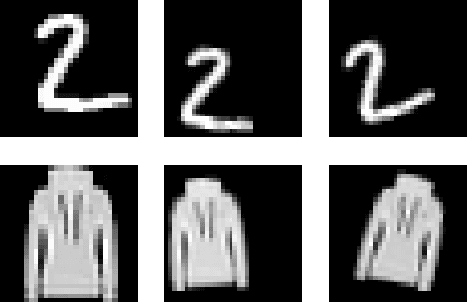
The problem of learning functions over spaces of probabilities - or distribution regression - is gaining significant interest in the machine learning community. A key challenge behind this problem is to identify a suitable representation capturing all relevant properties of the underlying functional mapping. A principled approach to distribution regression is provided by kernel mean embeddings, which lifts kernel-induced similarity on the input domain at the probability level. This strategy effectively tackles the two-stage sampling nature of the problem, enabling one to derive estimators with strong statistical guarantees, such as universal consistency and excess risk bounds. However, kernel mean embeddings implicitly hinge on the maximum mean discrepancy (MMD), a metric on probabilities, which may fail to capture key geometrical relations between distributions. In contrast, optimal transport (OT) metrics, are potentially more appealing, as documented by the recent literature on the topic. In this work, we propose the first OT-based estimator for distribution regression. We build on the Sliced Wasserstein distance to obtain an OT-based representation. We study the theoretical properties of a kernel ridge regression estimator based on such representation, for which we prove universal consistency and excess risk bounds. Preliminary experiments complement our theoretical findings by showing the effectiveness of the proposed approach and compare it with MMD-based estimators.

The Role of Global Labels in Few-Shot Classification and How to Infer Them

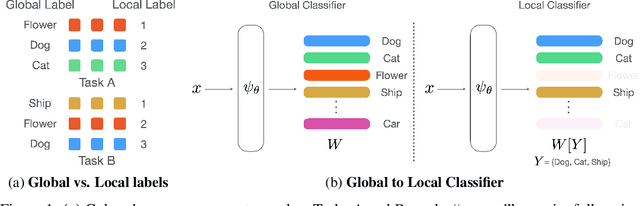
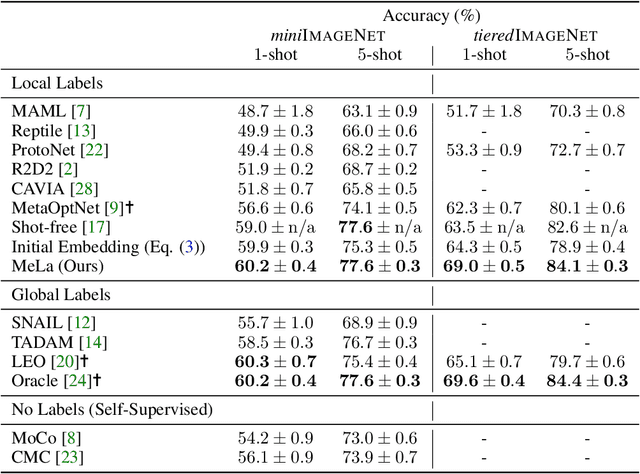
Few-shot learning (FSL) is a central problem in meta-learning, where learners must quickly adapt to new tasks given limited training data. Surprisingly, recent works have outperformed meta-learning methods tailored to FSL by casting it as standard supervised learning to jointly classify all classes shared across tasks. However, this approach violates the standard FSL setting by requiring global labels shared across tasks, which are often unavailable in practice. In this paper, we show why solving FSL via standard classification is theoretically advantageous. This motivates us to propose Meta Label Learning (MeLa), a novel algorithm that infers global labels and obtains robust few-shot models via standard classification. Empirically, we demonstrate that MeLa outperforms meta-learning competitors and is comparable to the oracle setting where ground truth labels are given. We provide extensive ablation studies to highlight the key properties of the proposed strategy.