Generalization of Hamiltonian algorithms

The paper proves generalization results for a class of stochastic learning algorithms. The method applies whenever the algorithm generates an absolutely continuous distribution relative to some a-priori measure and the Radon Nikodym derivative has subgaussian concentration. Applications are bounds for the Gibbs algorithm and randomizations of stable deterministic algorithms as well as PAC-Bayesian bounds with data-dependent priors.

Generalization for slowly mixing processes

A bound uniform over various loss-classes is given for data generated by stationary and phi-mixing processes, where the mixing time (the time needed to obtain approximate independence) enters the sample complexity only in an additive way. For slowly mixing processes this can be a considerable advantage over results with multiplicative dependence on the mixing time. The admissible loss-classes include functions with prescribed Lipschitz norms or smoothness parameters. The bound can also be applied to be uniform over unconstrained loss-classes, where it depends on local Lipschitz properties of the function on the sample path.

Learning Dynamical Systems via Koopman Operator Regression in Reproducing Kernel Hilbert Spaces

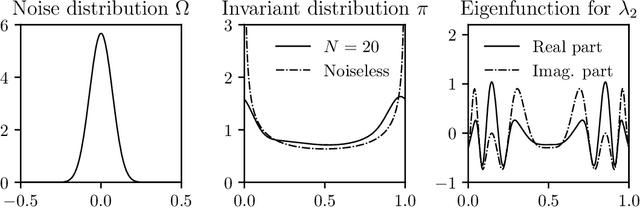
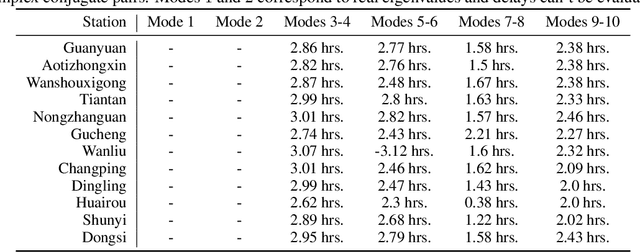
We study a class of dynamical systems modelled as Markov chains that admit an invariant distribution via the corresponding transfer, or Koopman, operator. While data-driven algorithms to reconstruct such operators are well known, their relationship with statistical learning is largely unexplored. We formalize a framework to learn the Koopman operator from finite data trajectories of the dynamical system. We consider the restriction of this operator to a reproducing kernel Hilbert space and introduce a notion of risk, from which different estimators naturally arise. We link the risk with the estimation of the spectral decomposition of the Koopman operator. These observations motivate a reduced-rank operator regression (RRR) estimator. We derive learning bounds for the proposed estimator, holding both in i.i.d. and non i.i.d. settings, the latter in terms of mixing coefficients. Our results suggest RRR might be beneficial over other widely used estimators as confirmed in numerical experiments both for forecasting and mode decomposition.

Some Hoeffding- and Bernstein-type Concentration Inequalities

We prove concentration inequalities for functions of independent random variables {under} sub-gaussian and sub-exponential conditions. The utility of the inequalities is demonstrated by an extension of the now classical method of Rademacher complexities to Lipschitz function classes and unbounded sub-exponential distribution.

A Perturbation Resilient Framework for Unsupervised Learning

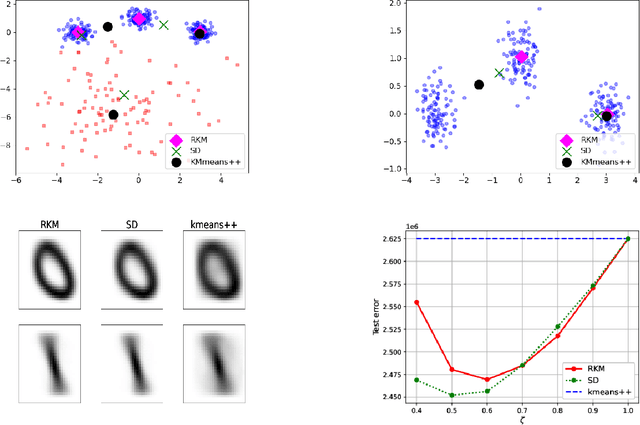
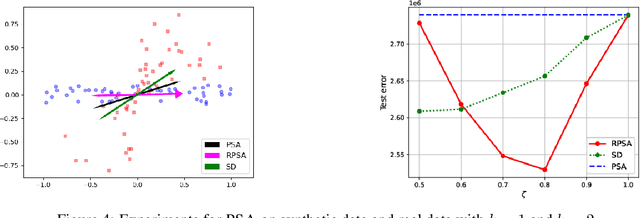
Designing learning algorithms that are resistant to perturbations of the underlying data distribution is a problem of wide practical and theoretical importance. We present a general approach to this problem focusing on unsupervised learning. The key assumption is that the perturbing distribution is characterized by larger losses relative to a given class of admissible models. This is exploited by a general descent algorithm which minimizes an $L$-statistic criterion over the model class, weighting more small losses. We characterize the robustness of the method in terms of bounds on the reconstruction error for the assumed unperturbed distribution. Numerical experiments with \textsc{kmeans} clustering and principal subspace analysis demonstrate the effectiveness of our method.

Learning Fair and Transferable Representations

Developing learning methods which do not discriminate subgroups in the population is a central goal of algorithmic fairness. One way to reach this goal is by modifying the data representation in order to meet certain fairness constraints. In this work we measure fairness according to demographic parity. This requires the probability of the possible model decisions to be independent of the sensitive information. We argue that the goal of imposing demographic parity can be substantially facilitated within a multitask learning setting. We leverage task similarities by encouraging a shared fair representation across the tasks via low rank matrix factorization. We derive learning bounds establishing that the learned representation transfers well to novel tasks both in terms of prediction performance and fairness metrics. We present experiments on three real world datasets, showing that the proposed method outperforms state-of-the-art approaches by a significant margin.

Uniform concentration and symmetrization for weak interactions

The method to derive uniform bounds with Gaussian and Rademacher complexities is extended to the case where the sample average is replaced by a nonlinear statistic. Tight bounds are obtained for U-statistics, smoothened L-statistics and error functionals of l2-regularized algorithms.

Empirical bounds for functions with weak interactions

We provide sharp empirical estimates of expectation, variance and normal approximation for a class of statistics whose variation in any argument does not change too much when another argument is modified. Examples of such weak interactions are furnished by U- and V-statistics, Lipschitz L-statistics and various error functionals of L2-regularized algorithms and Gibbs algorithms.

Bounds for Vector-Valued Function Estimation

We present a framework to derive risk bounds for vector-valued learning with a broad class of feature maps and loss functions. Multi-task learning and one-vs-all multi-category learning are treated as examples. We discuss in detail vector-valued functions with one hidden layer, and demonstrate that the conditions under which shared representations are beneficial for multi- task learning are equally applicable to multi-category learning.

A vector-contraction inequality for Rademacher complexities

The contraction inequality for Rademacher averages is extended to Lipschitz functions with vector-valued domains, and it is also shown that in the bounding expression the Rademacher variables can be replaced by arbitrary iid symmetric and sub-gaussian variables. Example applications are given for multi-category learning, K-means clustering and learning-to-learn.