kooplearn: A Scikit-Learn Compatible Library of Algorithms for Evolution Operator Learning

kooplearn is a machine-learning library that implements linear, kernel, and deep-learning estimators of dynamical operators and their spectral decompositions. kooplearn can model both discrete-time evolution operators (Koopman/Transfer) and continuous-time infinitesimal generators. By learning these operators, users can analyze dynamical systems via spectral methods, derive data-driven reduced-order models, and forecast future states and observables. kooplearn's interface is compliant with the scikit-learn API, facilitating its integration into existing machine learning and data science workflows. Additionally, kooplearn includes curated benchmark datasets to support experimentation, reproducibility, and the fair comparison of learning algorithms. The software is available at https://github.com/Machine-Learning-Dynamical-Systems/kooplearn.

Self-Supervised Evolution Operator Learning for High-Dimensional Dynamical Systems

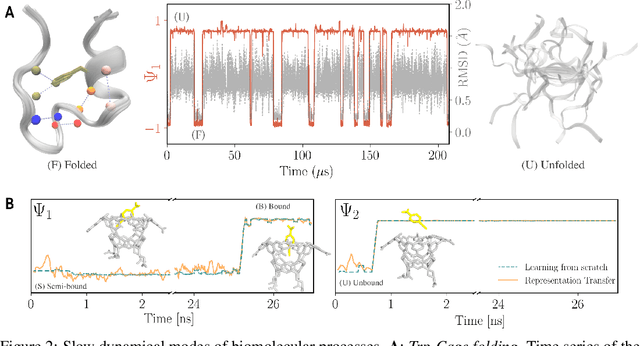
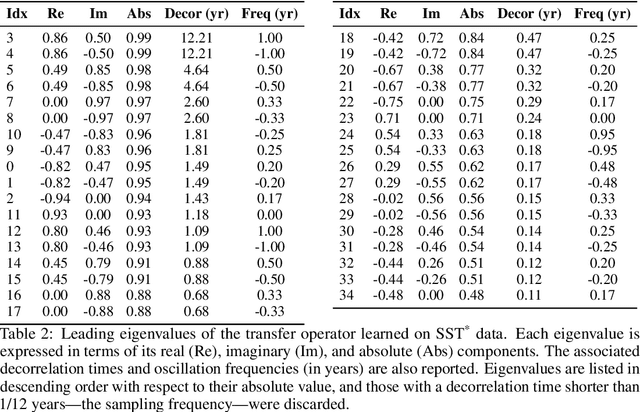
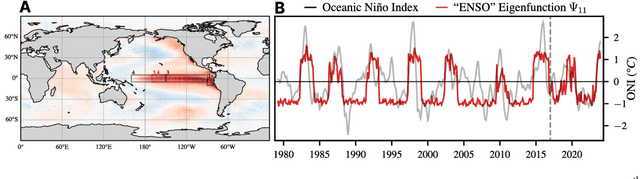
We introduce an encoder-only approach to learn the evolution operators of large-scale non-linear dynamical systems, such as those describing complex natural phenomena. Evolution operators are particularly well-suited for analyzing systems that exhibit complex spatio-temporal patterns and have become a key analytical tool across various scientific communities. As terabyte-scale weather datasets and simulation tools capable of running millions of molecular dynamics steps per day are becoming commodities, our approach provides an effective tool to make sense of them from a data-driven perspective. The core of it lies in a remarkable connection between self-supervised representation learning methods and the recently established learning theory of evolution operators. To show the usefulness of the proposed method, we test it across multiple scientific domains: explaining the folding dynamics of small proteins, the binding process of drug-like molecules in host sites, and autonomously finding patterns in climate data. Code and data to reproduce the experiments are made available open source.

Laplace Transform Based Low-Complexity Learning of Continuous Markov Semigroups

Markov processes serve as a universal model for many real-world random processes. This paper presents a data-driven approach for learning these models through the spectral decomposition of the infinitesimal generator (IG) of the Markov semigroup. The unbounded nature of IGs complicates traditional methods such as vector-valued regression and Hilbert-Schmidt operator analysis. Existing techniques, including physics-informed kernel regression, are computationally expensive and limited in scope, with no recovery guarantees for transfer operator methods when the time-lag is small. We propose a novel method that leverages the IG's resolvent, characterized by the Laplace transform of transfer operators. This approach is robust to time-lag variations, ensuring accurate eigenvalue learning even for small time-lags. Our statistical analysis applies to a broader class of Markov processes than current methods while reducing computational complexity from quadratic to linear in the state dimension. Finally, we illustrate the behaviour of our method in two experiments.

Neural Conditional Probability for Inference

We introduce NCP (Neural Conditional Probability), a novel operator-theoretic approach for learning conditional distributions with a particular focus on inference tasks. NCP can be used to build conditional confidence regions and extract important statistics like conditional quantiles, mean, and covariance. It offers streamlined learning through a single unconditional training phase, facilitating efficient inference without the need for retraining even when conditioning changes. By tapping into the powerful approximation capabilities of neural networks, our method efficiently handles a wide variety of complex probability distributions, effectively dealing with nonlinear relationships between input and output variables. Theoretical guarantees ensure both optimization consistency and statistical accuracy of the NCP method. Our experiments show that our approach matches or beats leading methods using a simple Multi-Layer Perceptron (MLP) with two hidden layers and GELU activations. This demonstrates that a minimalistic architecture with a theoretically grounded loss function can achieve competitive results without sacrificing performance, even in the face of more complex architectures.

Operator World Models for Reinforcement Learning

Policy Mirror Descent (PMD) is a powerful and theoretically sound methodology for sequential decision-making. However, it is not directly applicable to Reinforcement Learning (RL) due to the inaccessibility of explicit action-value functions. We address this challenge by introducing a novel approach based on learning a world model of the environment using conditional mean embeddings. We then leverage the operatorial formulation of RL to express the action-value function in terms of this quantity in closed form via matrix operations. Combining these estimators with PMD leads to POWR, a new RL algorithm for which we prove convergence rates to the global optimum. Preliminary experiments in finite and infinite state settings support the effectiveness of our method.

A randomized algorithm to solve reduced rank operator regression

We present and analyze an algorithm designed for addressing vector-valued regression problems involving possibly infinite-dimensional input and output spaces. The algorithm is a randomized adaptation of reduced rank regression, a technique to optimally learn a low-rank vector-valued function (i.e. an operator) between sampled data via regularized empirical risk minimization with rank constraints. We propose Gaussian sketching techniques both for the primal and dual optimization objectives, yielding Randomized Reduced Rank Regression (R4) estimators that are efficient and accurate. For each of our R4 algorithms we prove that the resulting regularized empirical risk is, in expectation w.r.t. randomness of a sketch, arbitrarily close to the optimal value when hyper-parameteres are properly tuned. Numerical expreriments illustrate the tightness of our bounds and show advantages in two distinct scenarios: (i) solving a vector-valued regression problem using synthetic and large-scale neuroscience datasets, and (ii) regressing the Koopman operator of a nonlinear stochastic dynamical system.

Consistent Long-Term Forecasting of Ergodic Dynamical Systems

We study the evolution of distributions under the action of an ergodic dynamical system, which may be stochastic in nature. By employing tools from Koopman and transfer operator theory one can evolve any initial distribution of the state forward in time, and we investigate how estimators of these operators perform on long-term forecasting. Motivated by the observation that standard estimators may fail at this task, we introduce a learning paradigm that neatly combines classical techniques of eigenvalue deflation from operator theory and feature centering from statistics. This paradigm applies to any operator estimator based on empirical risk minimization, making them satisfy learning bounds which hold uniformly on the entire trajectory of future distributions, and abide to the conservation of mass for each of the forecasted distributions. Numerical experiments illustrates the advantages of our approach in practice.

Dynamics Harmonic Analysis of Robotic Systems: Application in Data-Driven Koopman Modelling

We introduce the use of harmonic analysis to decompose the state space of symmetric robotic systems into orthogonal isotypic subspaces. These are lower-dimensional spaces that capture distinct, symmetric, and synergistic motions. For linear dynamics, we characterize how this decomposition leads to a subdivision of the dynamics into independent linear systems on each subspace, a property we term dynamics harmonic analysis (DHA). To exploit this property, we use Koopman operator theory to propose an equivariant deep-learning architecture that leverages the properties of DHA to learn a global linear model of system dynamics. Our architecture, validated on synthetic systems and the dynamics of locomotion of a quadrupedal robot, demonstrates enhanced generalization, sample efficiency, and interpretability, with less trainable parameters and computational costs.

Deep projection networks for learning time-homogeneous dynamical systems

We consider the general class of time-homogeneous dynamical systems, both discrete and continuous, and study the problem of learning a meaningful representation of the state from observed data. This is instrumental for the task of learning a forward transfer operator of the system, that in turn can be used for forecasting future states or observables. The representation, typically parametrized via a neural network, is associated with a projection operator and is learned by optimizing an objective function akin to that of canonical correlation analysis (CCA). However, unlike CCA, our objective avoids matrix inversions and therefore is generally more stable and applicable to challenging scenarios. Our objective is a tight relaxation of CCA and we further enhance it by proposing two regularization schemes, one encouraging the orthogonality of the components of the representation while the other exploiting Chapman-Kolmogorov's equation. We apply our method to challenging discrete dynamical systems, discussing improvements over previous methods, as well as to continuous dynamical systems.

Estimating Koopman operators with sketching to provably learn large scale dynamical systems

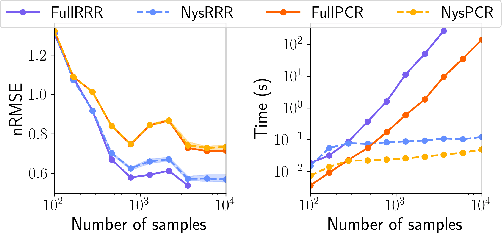
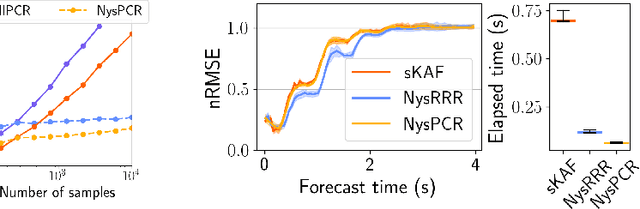
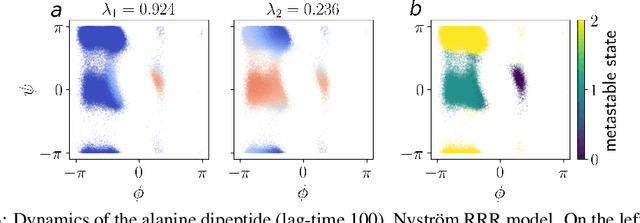
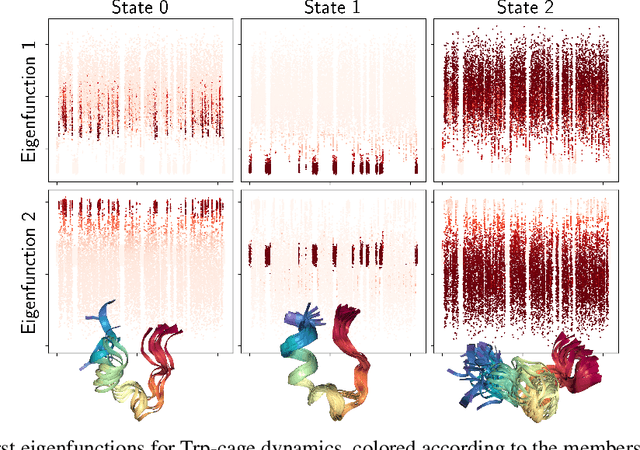
The theory of Koopman operators allows to deploy non-parametric machine learning algorithms to predict and analyze complex dynamical systems. Estimators such as principal component regression (PCR) or reduced rank regression (RRR) in kernel spaces can be shown to provably learn Koopman operators from finite empirical observations of the system's time evolution. Scaling these approaches to very long trajectories is a challenge and requires introducing suitable approximations to make computations feasible. In this paper, we boost the efficiency of different kernel-based Koopman operator estimators using random projections (sketching). We derive, implement and test the new "sketched" estimators with extensive experiments on synthetic and large-scale molecular dynamics datasets. Further, we establish non asymptotic error bounds giving a sharp characterization of the trade-offs between statistical learning rates and computational efficiency. Our empirical and theoretical analysis shows that the proposed estimators provide a sound and efficient way to learn large scale dynamical systems. In particular our experiments indicate that the proposed estimators retain the same accuracy of PCR or RRR, while being much faster.