Leveraging Symmetry in RL-based Legged Locomotion Control

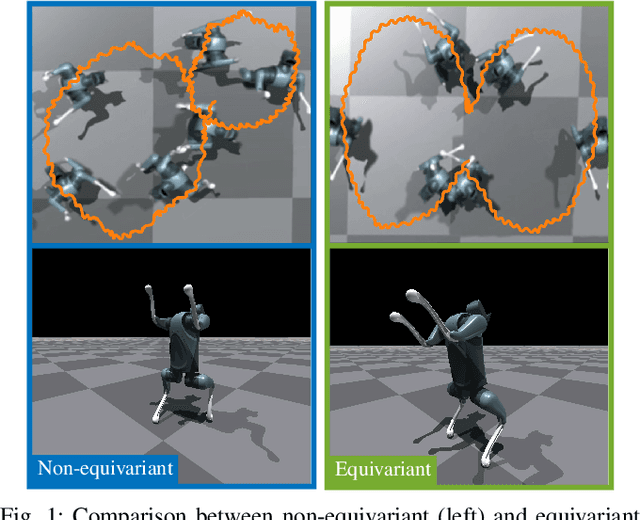
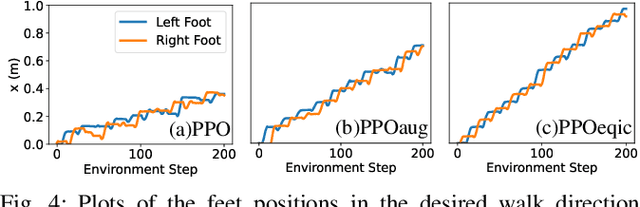
Model-free reinforcement learning is a promising approach for autonomously solving challenging robotics control problems, but faces exploration difficulty without information of the robot's kinematics and dynamics morphology. The under-exploration of multiple modalities with symmetric states leads to behaviors that are often unnatural and sub-optimal. This issue becomes particularly pronounced in the context of robotic systems with morphological symmetries, such as legged robots for which the resulting asymmetric and aperiodic behaviors compromise performance, robustness, and transferability to real hardware. To mitigate this challenge, we can leverage symmetry to guide and improve the exploration in policy learning via equivariance/invariance constraints. In this paper, we investigate the efficacy of two approaches to incorporate symmetry: modifying the network architectures to be strictly equivariant/invariant, and leveraging data augmentation to approximate equivariant/invariant actor-critics. We implement the methods on challenging loco-manipulation and bipedal locomotion tasks and compare with an unconstrained baseline. We find that the strictly equivariant policy consistently outperforms other methods in sample efficiency and task performance in simulation. In addition, symmetry-incorporated approaches exhibit better gait quality, higher robustness and can be deployed zero-shot in real-world experiments.

Morphological Symmetries in Robotics

We present a comprehensive framework for studying and leveraging morphological symmetries in robotic systems. These are intrinsic properties of the robot's morphology, frequently observed in animal biology and robotics, which stem from the replication of kinematic structures and the symmetrical distribution of mass. We illustrate how these symmetries extend to the robot's state space and both proprioceptive and exteroceptive sensor measurements, resulting in the equivariance of the robot's equations of motion and optimal control policies. Thus, we recognize morphological symmetries as a relevant and previously unexplored physics-informed geometric prior, with significant implications for both data-driven and analytical methods used in modeling, control, estimation and design in robotics. For data-driven methods, we demonstrate that morphological symmetries can enhance the sample efficiency and generalization of machine learning models through data augmentation, or by applying equivariant/invariant constraints on the model's architecture. In the context of analytical methods, we employ abstract harmonic analysis to decompose the robot's dynamics into a superposition of lower-dimensional, independent dynamics. We substantiate our claims with both synthetic and real-world experiments conducted on bipedal and quadrupedal robots. Lastly, we introduce the repository MorphoSymm to facilitate the practical use of the theory and applications outlined in this work.

Dynamics Harmonic Analysis of Robotic Systems: Application in Data-Driven Koopman Modelling

We introduce the use of harmonic analysis to decompose the state space of symmetric robotic systems into orthogonal isotypic subspaces. These are lower-dimensional spaces that capture distinct, symmetric, and synergistic motions. For linear dynamics, we characterize how this decomposition leads to a subdivision of the dynamics into independent linear systems on each subspace, a property we term dynamics harmonic analysis (DHA). To exploit this property, we use Koopman operator theory to propose an equivariant deep-learning architecture that leverages the properties of DHA to learn a global linear model of system dynamics. Our architecture, validated on synthetic systems and the dynamics of locomotion of a quadrupedal robot, demonstrates enhanced generalization, sample efficiency, and interpretability, with less trainable parameters and computational costs.