Multi-Contact Inertial Estimation and Localization in Legged Robots

Optimal estimation is a promising tool for multi-contact inertial estimation and localization. To harness its advantages in robotics, it is crucial to solve these large and challenging optimization problems efficiently. To tackle this, we (i) develop a multiple-shooting solver that exploits both temporal and parametric structures through a parametrized Riccati recursion. Additionally, we (ii) propose an inertial local manifold that ensures its full physical consistency. It also enhances convergence compared to the singularity-free log-Cholesky approach. To handle its singularities, we (iii) introduce a nullspace approach in our optimal estimation solver. We (iv) finally develop the analytical derivatives of contact dynamics for both inertial parametrizations. Our framework can successfully solve estimation problems for complex maneuvers such as brachiation in humanoids. We demonstrate its numerical capabilities across various robotics tasks and its benefits in experimental trials with the Go1 robot.

Morphological Symmetries in Robotics

We present a comprehensive framework for studying and leveraging morphological symmetries in robotic systems. These are intrinsic properties of the robot's morphology, frequently observed in animal biology and robotics, which stem from the replication of kinematic structures and the symmetrical distribution of mass. We illustrate how these symmetries extend to the robot's state space and both proprioceptive and exteroceptive sensor measurements, resulting in the equivariance of the robot's equations of motion and optimal control policies. Thus, we recognize morphological symmetries as a relevant and previously unexplored physics-informed geometric prior, with significant implications for both data-driven and analytical methods used in modeling, control, estimation and design in robotics. For data-driven methods, we demonstrate that morphological symmetries can enhance the sample efficiency and generalization of machine learning models through data augmentation, or by applying equivariant/invariant constraints on the model's architecture. In the context of analytical methods, we employ abstract harmonic analysis to decompose the robot's dynamics into a superposition of lower-dimensional, independent dynamics. We substantiate our claims with both synthetic and real-world experiments conducted on bipedal and quadrupedal robots. Lastly, we introduce the repository MorphoSymm to facilitate the practical use of the theory and applications outlined in this work.

Dynamics Harmonic Analysis of Robotic Systems: Application in Data-Driven Koopman Modelling

We introduce the use of harmonic analysis to decompose the state space of symmetric robotic systems into orthogonal isotypic subspaces. These are lower-dimensional spaces that capture distinct, symmetric, and synergistic motions. For linear dynamics, we characterize how this decomposition leads to a subdivision of the dynamics into independent linear systems on each subspace, a property we term dynamics harmonic analysis (DHA). To exploit this property, we use Koopman operator theory to propose an equivariant deep-learning architecture that leverages the properties of DHA to learn a global linear model of system dynamics. Our architecture, validated on synthetic systems and the dynamics of locomotion of a quadrupedal robot, demonstrates enhanced generalization, sample efficiency, and interpretability, with less trainable parameters and computational costs.

Optimal Control for Articulated Soft Robots

Soft robots can execute tasks with safer interactions. However, control techniques that can effectively exploit the systems' capabilities are still missing. Differential dynamic programming (DDP) has emerged as a promising tool for achieving highly dynamic tasks. But most of the literature deals with applying DDP to articulated soft robots by using numerical differentiation, in addition to using pure feed-forward control to perform explosive tasks. Further, underactuated compliant robots are known to be difficult to control and the use of DDP-based algorithms to control them is not yet addressed. We propose an efficient DDP-based algorithm for trajectory optimization of articulated soft robots that can optimize the state trajectory, input torques, and stiffness profile. We provide an efficient method to compute the forward dynamics and the analytical derivatives of series elastic actuators (SEA)/variable stiffness actuators (VSA) and underactuated compliant robots. We present a state-feedback controller that uses locally optimal feedback policies obtained from DDP. We show through simulations and experiments that the use of feedback is crucial in improving the performance and stabilization properties of various tasks. We also show that the proposed method can be used to plan and control underactuated compliant robots, with varying degrees of underactuation effectively.

Perceptive Locomotion through Whole-Body MPC and Optimal Region Selection

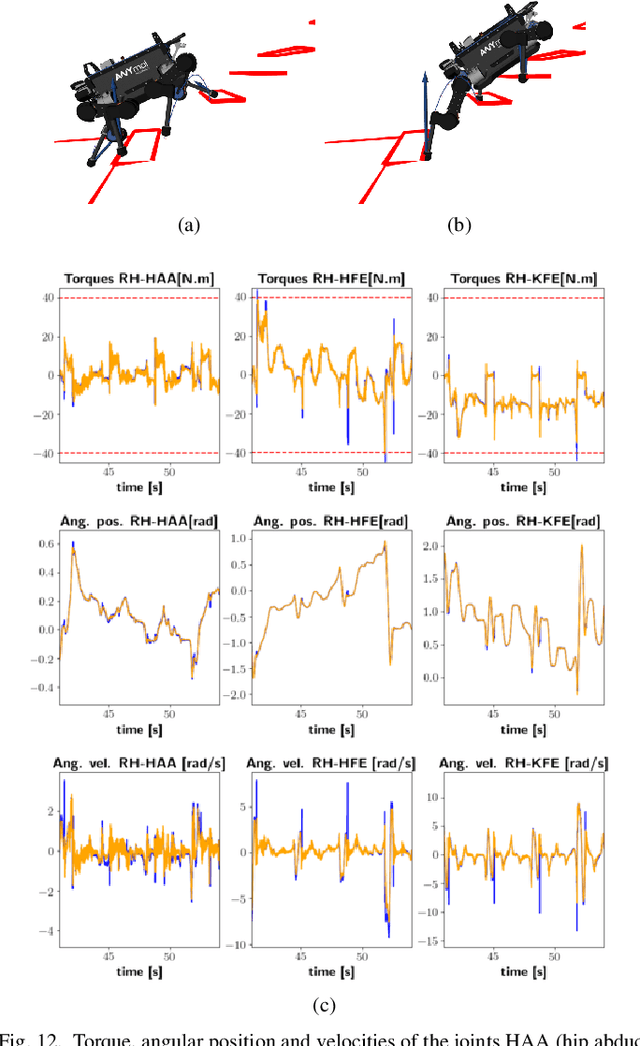
Real-time synthesis of legged locomotion maneuvers in challenging industrial settings is still an open problem, requiring simultaneous determination of footsteps locations several steps ahead while generating whole-body motions close to the robot's limits. State estimation and perception errors impose the practical constraint of fast re-planning motions in a model predictive control (MPC) framework. We first observe that the computational limitation of perceptive locomotion pipelines lies in the combinatorics of contact surface selection. Re-planning contact locations on selected surfaces can be accomplished at MPC frequencies (50-100 Hz). Then, whole-body motion generation typically follows a reference trajectory for the robot base to facilitate convergence. We propose removing this constraint to robustly address unforeseen events such as contact slipping, by leveraging a state-of-the-art whole-body MPC (Croccodyl). Our contributions are integrated into a complete framework for perceptive locomotion, validated under diverse terrain conditions, and demonstrated in challenging trials that push the robot's actuation limits, as well as in the ICRA 2023 quadruped challenge simulation.

Topology-Based MPC for Automatic Footstep Placement and Contact Surface Selection

State-of-the-art approaches to footstep planning assume reduced-order dynamics when solving the combinatorial problem of selecting contact surfaces in real time. However, in exchange for computational efficiency, these approaches ignore joint torque limits and limb dynamics. In this work, we address these limitations by presenting a topology-based approach that enables~\gls{mpc} to simultaneously plan full-body motions, torque commands, footstep placements, and contact surfaces in real time. To determine if a robot's foot is inside a contact surface, we borrow the winding number concept from topology. We then use this winding number and potential field to create a contact-surface penalty function. By using this penalty function,~\gls{mpc} can select a contact surface from all candidate surfaces in the vicinity and determine footstep placements within it. We demonstrate the benefits of our approach by showing the impact of considering full-body dynamics, which includes joint torque limits and limb dynamics, on the selection of footstep placements and contact surfaces. Furthermore, we validate the feasibility of deploying our topology-based approach in an~\gls{mpc} scheme and explore its potential capabilities through a series of experimental and simulation trials.

Inverse-Dynamics MPC via Nullspace Resolution

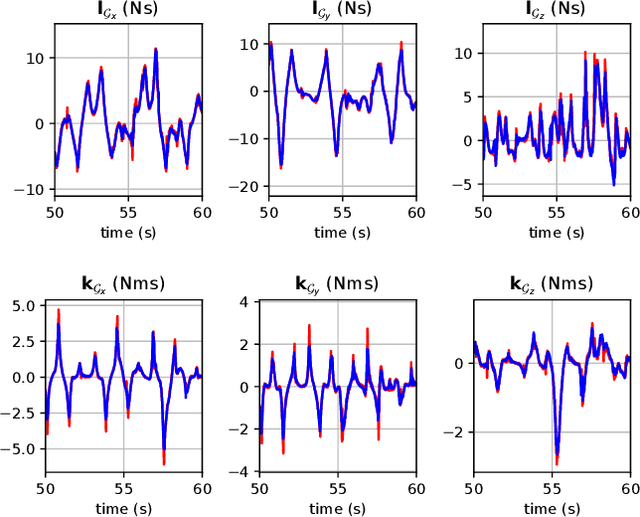
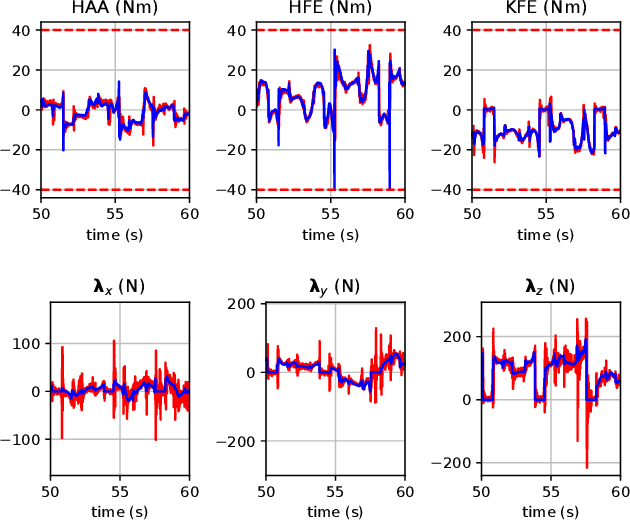
Optimal control (OC) using inverse dynamics provides numerical benefits such as coarse optimization, cheaper computation of derivatives, and a high convergence rate. However, in order to take advantage of these benefits in model predictive control (MPC) for legged robots, it is crucial to handle its large number of equality constraints efficiently. To accomplish this, we first (i) propose a novel approach to handle equality constraints based on nullspace parametrization. Our approach balances optimality, and both dynamics and equality-constraint feasibility appropriately, which increases the basin of attraction to good local minima. To do so, we then (ii) adapt our feasibility-driven search by incorporating a merit function. Furthermore, we introduce (iii) a condensed formulation of the inverse dynamics that considers arbitrary actuator models. We also develop (iv) a novel MPC based on inverse dynamics within a perception locomotion framework. Finally, we present (v) a theoretical comparison of optimal control with the forward and inverse dynamics, and evaluate both numerically. Our approach enables the first application of inverse-dynamics MPC on hardware, resulting in state-of-the-art dynamic climbing on the ANYmal robot. We benchmark it over a wide range of robotics problems and generate agile and complex maneuvers. We show the computational reduction of our nullspace resolution and condensed formulation (up to 47.3%). We provide evidence of the benefits of our approach by solving coarse optimization problems with a high convergence rate (up to 10 Hz of discretization). Our algorithm is publicly available inside CROCODDYL.

Differentiable Optimal Control via Differential Dynamic Programming

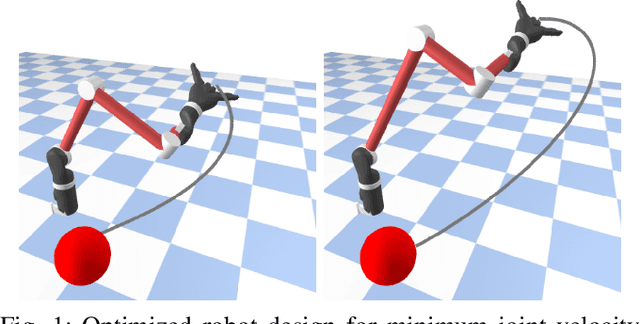
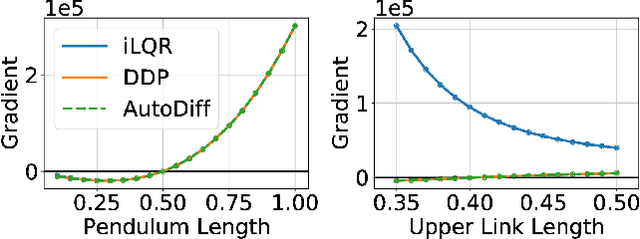
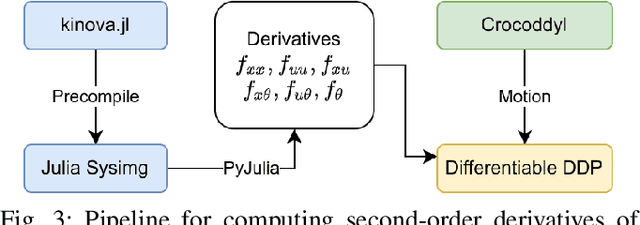
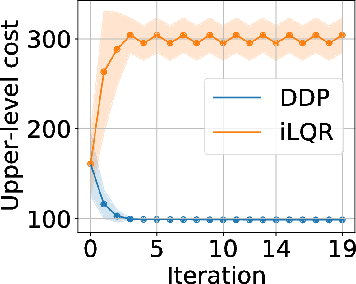
Robot design optimization, imitation learning and system identification share a common problem which requires optimization over robot or task parameters at the same time as optimizing the robot motion. To solve these problems, we can use differentiable optimal control for which the gradients of the robot's motion with respect to the parameters are required. We propose a method to efficiently compute these gradients analytically via the differential dynamic programming (DDP) algorithm using sensitivity analysis (SA). We show that we must include second-order dynamics terms when computing the gradients. However, we do not need to include them when computing the motion. We validate our approach on the pendulum and double pendulum systems. Furthermore, we compare against using the derivatives of the iterative linear quadratic regulator (iLQR), which ignores these second-order terms everywhere, on a co-design task for the Kinova arm, where we optimize the link lengths of the robot for a target reaching task. We show that optimizing using iLQR gradients diverges as ignoring the second-order dynamics affects the computation of the derivatives. Instead, optimizing using DDP gradients converges to the same optimum for a range of initial designs allowing our formulation to scale to complex systems.

Agile Maneuvers in Legged Robots: a Predictive Control Approach

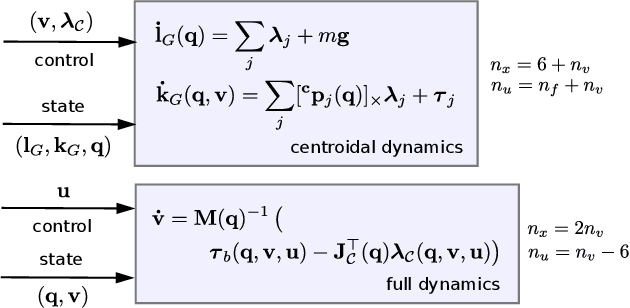
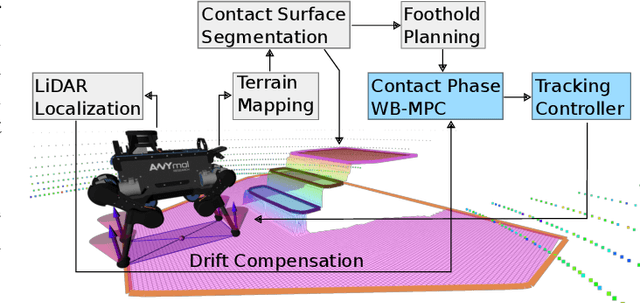
Achieving agile maneuvers through multiple contact phases has been a longstanding challenge in legged robotics. It requires to derive motion plans and local control feedback policies in real-time to handle the nonholonomy of the kinetic momenta. While a few recent predictive control approaches based on centroidal momentum have been able to generate dynamic motions, they assume unlimited actuation capabilities. This assumption is quite restrictive and does not hold for agile maneuvers on most robots. In this work, we present a contact-phase predictive and state-feedback controllers that enables legged robots to plan and perform agile locomotion skills. Our predictive controller models the contact phases using a hybrid paradigm that considers the robot's actuation limits and full dynamics. We demonstrate the benefits of our approach on agile maneuvers on ANYmal robots in realistic scenarios. To the best of our knowledge, our work is the first to show that predictive control can handle actuation limits, generate agile locomotion maneuvers and execute locally optimal feedback policies on hardware without the use of a separate whole-body controller.

Co-Designing Robots by Differentiating Motion Solvers

We present a novel algorithm for the computational co-design of legged robots and dynamic maneuvers. Current state-of-the-art approaches are based on random sampling or concurrent optimization. A few recently proposed methods explore the relationship between the gradient of the optimal motion and robot design. Inspired by these approaches, we propose a bilevel optimization approach that exploits the derivatives of the motion planning sub-problem (the inner level) without simplifying assumptions on its structure. Our approach can quickly optimize the robot's morphology while considering its full dynamics, joint limits and physical constraints such as friction cones. It has a faster convergence rate and greater scalability for larger design problems than state-of-the-art approaches based on sampling methods. It also allows us to handle constraints such as the actuation limits, which are important for co-designing dynamic maneuvers. We demonstrate these capabilities by studying jumping and trotting gaits under different design metrics and verify our results in a physics simulator. For these cases, our algorithm converges in less than a third of the number of iterations needed for sampling approaches, and the computation time scales linearly.