Explicit Contact Optimization in Whole-Body Contact-Rich Manipulation

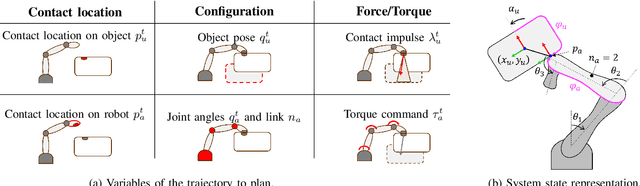
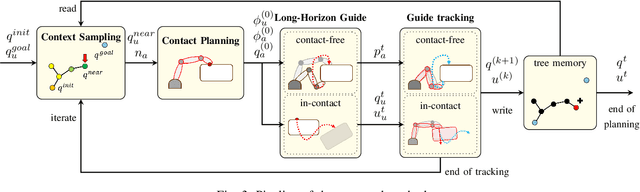
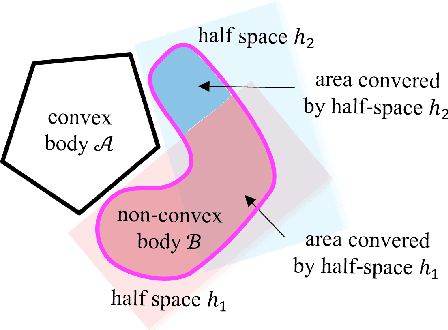
Humans can exploit contacts anywhere on their body surface to manipulate large and heavy items, objects normally out of reach or multiple objects at once. However, such manipulation through contacts using the whole surface of the body remains extremely challenging to achieve on robots. This can be labelled as Whole-Body Contact-Rich Manipulation (WBCRM) problem. In addition to the high-dimensionality of the Contact-Rich Manipulation problem due to the combinatorics of contact modes, admitting contact creation anywhere on the body surface adds complexity, which hinders planning of manipulation within a reasonable time. We address this computational problem by formulating the contact and motion planning of planar WBCRM as hierarchical continuous optimization problems. To enable this formulation, we propose a novel continuous explicit representation of the robot surface, that we believe to be foundational for future research using continuous optimization for WBCRM. Our results demonstrate a significant improvement of convergence, planning time and feasibility - with, on the average, 99% less iterations and 96% reduction in time to find a solution over considered scenarios, without recourse to prone-to-failure trajectory refinement steps.

NAS: N-step computation of All Solutions to the footstep planning problem

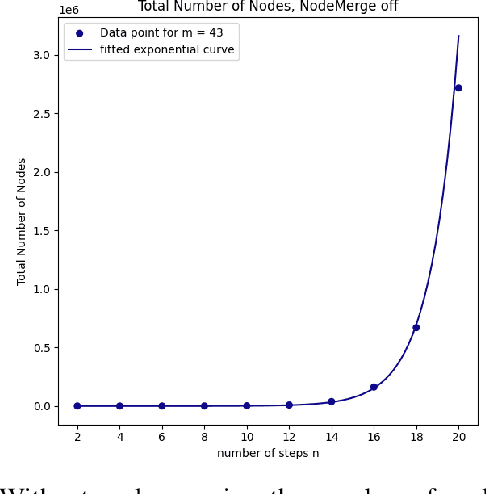
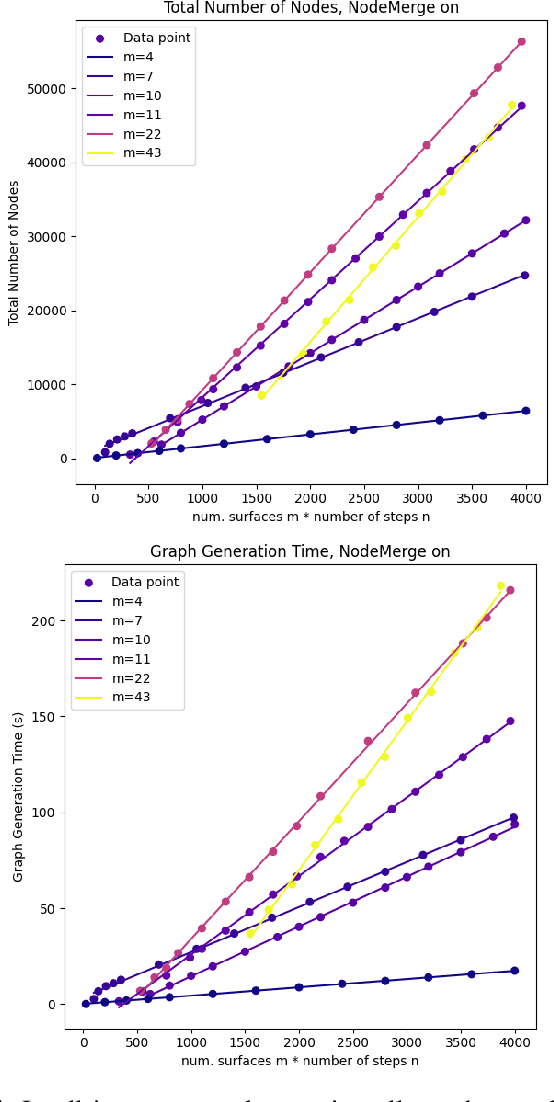
How many ways are there to climb a staircase in a given number of steps? Infinitely many, if we focus on the continuous aspect of the problem. A finite, possibly large number if we consider the discrete aspect, i.e. on which surface which effectors are going to step and in what order. We introduce NAS, an algorithm that considers both aspects simultaneously and computes all the possible solutions to such a contact planning problem, under standard assumptions. To our knowledge NAS is the first algorithm to produce a globally optimal policy, efficiently queried in real time for planning the next footsteps of a humanoid robot. Our empirical results (in simulation and on the Talos platform) demonstrate that, despite the theoretical exponential complexity, optimisations reduce the practical complexity of NAS to a manageable bilinear form, maintaining completeness guarantees and enabling efficient GPU parallelisation. NAS is demonstrated in a variety of scenarios for the Talos robot, both in simulation and on the hardware platform. Future work will focus on further reducing computation times and extending the algorithm's applicability beyond gaited locomotion. Our companion video is available at https://youtu.be/Shkf8PyDg4g

Online Multi-Contact Receding Horizon Planning via Value Function Approximation

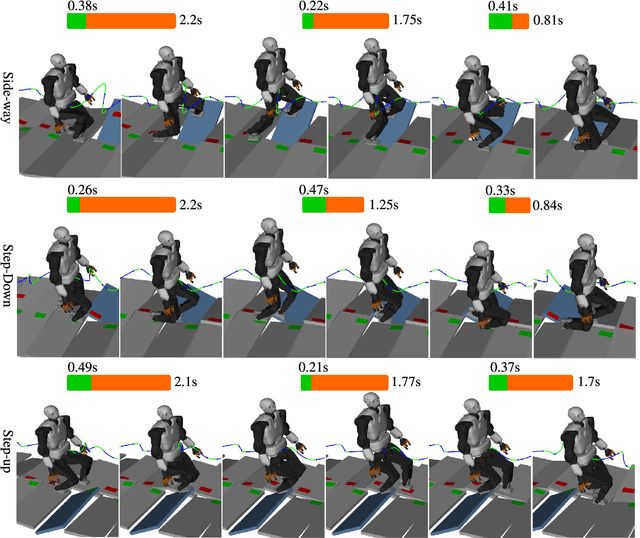
Planning multi-contact motions in a receding horizon fashion requires a value function to guide the planning with respect to the future, e.g., building momentum to traverse large obstacles. Traditionally, the value function is approximated by computing trajectories in a prediction horizon (never executed) that foresees the future beyond the execution horizon. However, given the non-convex dynamics of multi-contact motions, this approach is computationally expensive. To enable online Receding Horizon Planning (RHP) of multi-contact motions, we find efficient approximations of the value function. Specifically, we propose a trajectory-based and a learning-based approach. In the former, namely RHP with Multiple Levels of Model Fidelity, we approximate the value function by computing the prediction horizon with a convex relaxed model. In the latter, namely Locally-Guided RHP, we learn an oracle to predict local objectives for locomotion tasks, and we use these local objectives to construct local value functions for guiding a short-horizon RHP. We evaluate both approaches in simulation by planning centroidal trajectories of a humanoid robot walking on moderate slopes, and on large slopes where the robot cannot maintain static balance. Our results show that locally-guided RHP achieves the best computation efficiency (95\%-98.6\% cycles converge online). This computation advantage enables us to demonstrate online receding horizon planning of our real-world humanoid robot Talos walking in dynamic environments that change on-the-fly.

Neural Lyapunov and Optimal Control

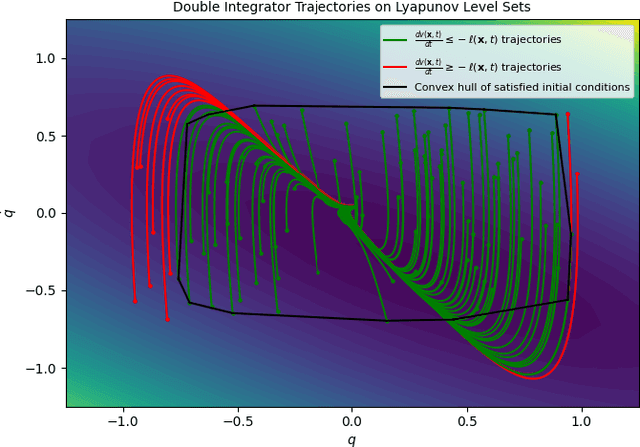
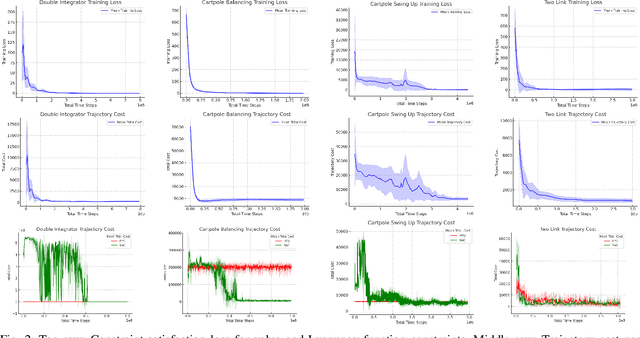
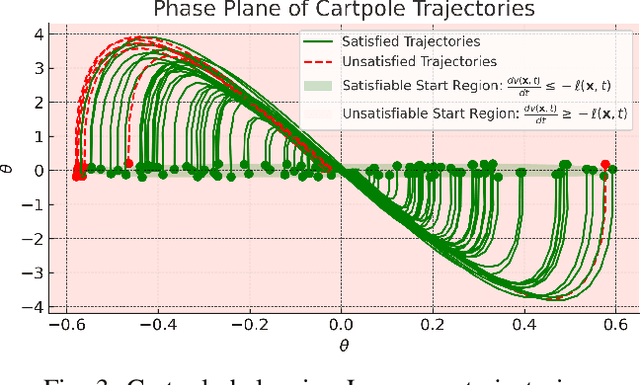
Optimal control (OC) is an effective approach to controlling complex dynamical systems. However, traditional approaches to parameterising and learning controllers in optimal control have been ad-hoc, collecting data and fitting it to neural networks. However, this can lead to learnt controllers ignoring constraints like optimality and time variability. We introduce a unified framework that simultaneously solves control problems while learning corresponding Lyapunov or value functions. Our method formulates OC-like mathematical programs based on the Hamilton-Jacobi-Bellman (HJB) equation. We leverage the HJB optimality constraint and its relaxation to learn time-varying value and Lyapunov functions, implicitly ensuring the inclusion of constraints. We show the effectiveness of our approach on linear and nonlinear control-affine problems. Additionally, we demonstrate significant reductions in planning horizons (up to a factor of 25) when incorporating the learnt functions into Model Predictive Controllers.

Perceptive Locomotion through Whole-Body MPC and Optimal Region Selection

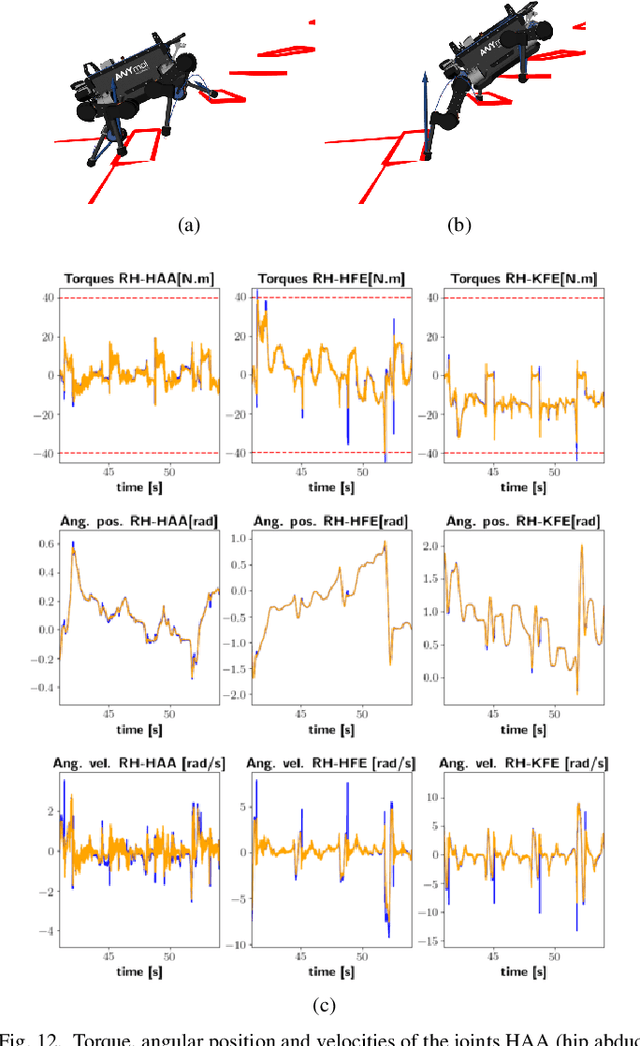
Real-time synthesis of legged locomotion maneuvers in challenging industrial settings is still an open problem, requiring simultaneous determination of footsteps locations several steps ahead while generating whole-body motions close to the robot's limits. State estimation and perception errors impose the practical constraint of fast re-planning motions in a model predictive control (MPC) framework. We first observe that the computational limitation of perceptive locomotion pipelines lies in the combinatorics of contact surface selection. Re-planning contact locations on selected surfaces can be accomplished at MPC frequencies (50-100 Hz). Then, whole-body motion generation typically follows a reference trajectory for the robot base to facilitate convergence. We propose removing this constraint to robustly address unforeseen events such as contact slipping, by leveraging a state-of-the-art whole-body MPC (Croccodyl). Our contributions are integrated into a complete framework for perceptive locomotion, validated under diverse terrain conditions, and demonstrated in challenging trials that push the robot's actuation limits, as well as in the ICRA 2023 quadruped challenge simulation.

Topology-Based MPC for Automatic Footstep Placement and Contact Surface Selection

State-of-the-art approaches to footstep planning assume reduced-order dynamics when solving the combinatorial problem of selecting contact surfaces in real time. However, in exchange for computational efficiency, these approaches ignore joint torque limits and limb dynamics. In this work, we address these limitations by presenting a topology-based approach that enables~\gls{mpc} to simultaneously plan full-body motions, torque commands, footstep placements, and contact surfaces in real time. To determine if a robot's foot is inside a contact surface, we borrow the winding number concept from topology. We then use this winding number and potential field to create a contact-surface penalty function. By using this penalty function,~\gls{mpc} can select a contact surface from all candidate surfaces in the vicinity and determine footstep placements within it. We demonstrate the benefits of our approach by showing the impact of considering full-body dynamics, which includes joint torque limits and limb dynamics, on the selection of footstep placements and contact surfaces. Furthermore, we validate the feasibility of deploying our topology-based approach in an~\gls{mpc} scheme and explore its potential capabilities through a series of experimental and simulation trials.

Inverse-Dynamics MPC via Nullspace Resolution

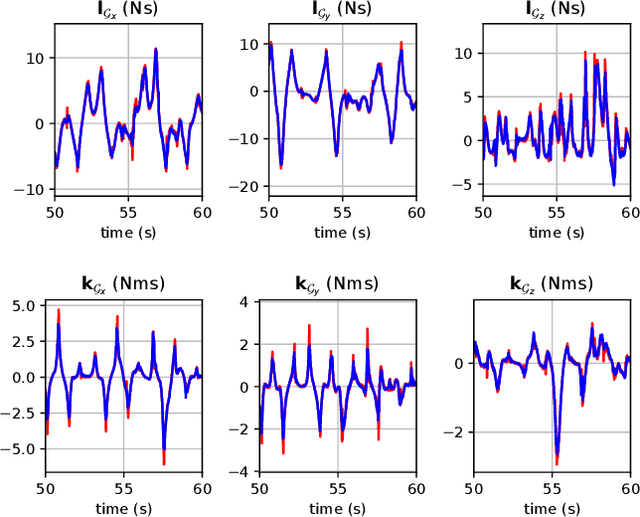
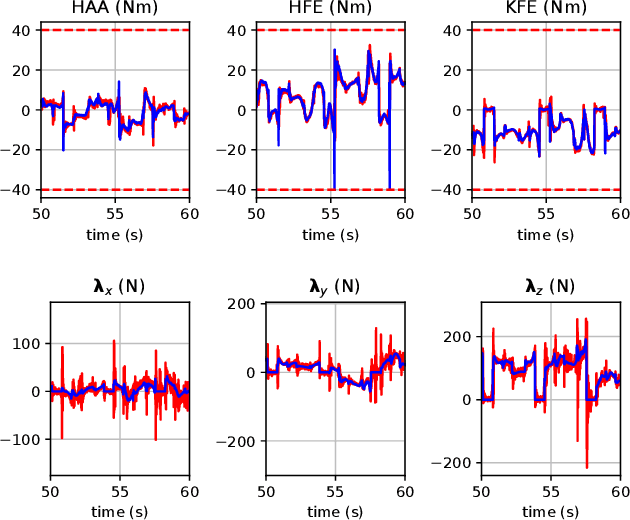
Optimal control (OC) using inverse dynamics provides numerical benefits such as coarse optimization, cheaper computation of derivatives, and a high convergence rate. However, in order to take advantage of these benefits in model predictive control (MPC) for legged robots, it is crucial to handle its large number of equality constraints efficiently. To accomplish this, we first (i) propose a novel approach to handle equality constraints based on nullspace parametrization. Our approach balances optimality, and both dynamics and equality-constraint feasibility appropriately, which increases the basin of attraction to good local minima. To do so, we then (ii) adapt our feasibility-driven search by incorporating a merit function. Furthermore, we introduce (iii) a condensed formulation of the inverse dynamics that considers arbitrary actuator models. We also develop (iv) a novel MPC based on inverse dynamics within a perception locomotion framework. Finally, we present (v) a theoretical comparison of optimal control with the forward and inverse dynamics, and evaluate both numerically. Our approach enables the first application of inverse-dynamics MPC on hardware, resulting in state-of-the-art dynamic climbing on the ANYmal robot. We benchmark it over a wide range of robotics problems and generate agile and complex maneuvers. We show the computational reduction of our nullspace resolution and condensed formulation (up to 47.3%). We provide evidence of the benefits of our approach by solving coarse optimization problems with a high convergence rate (up to 10 Hz of discretization). Our algorithm is publicly available inside CROCODDYL.

Differentiable Optimal Control via Differential Dynamic Programming

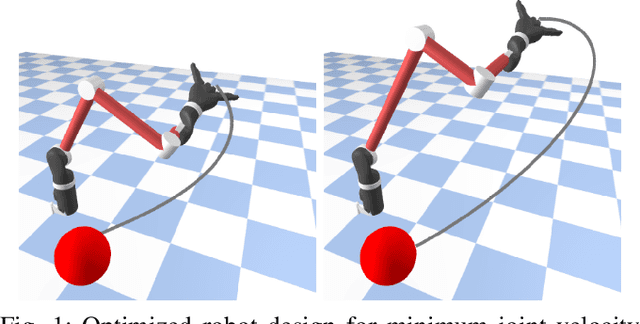
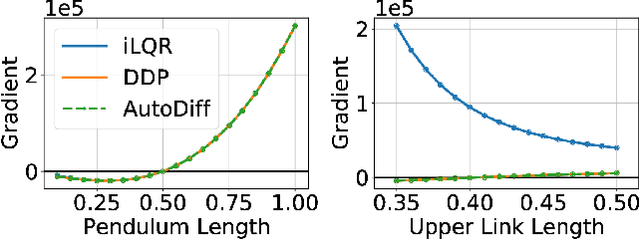
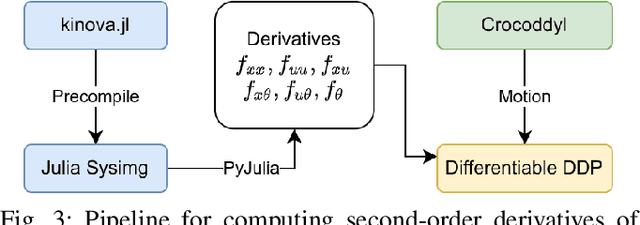
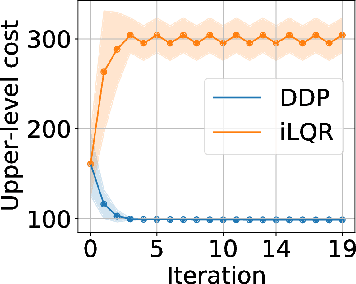
Robot design optimization, imitation learning and system identification share a common problem which requires optimization over robot or task parameters at the same time as optimizing the robot motion. To solve these problems, we can use differentiable optimal control for which the gradients of the robot's motion with respect to the parameters are required. We propose a method to efficiently compute these gradients analytically via the differential dynamic programming (DDP) algorithm using sensitivity analysis (SA). We show that we must include second-order dynamics terms when computing the gradients. However, we do not need to include them when computing the motion. We validate our approach on the pendulum and double pendulum systems. Furthermore, we compare against using the derivatives of the iterative linear quadratic regulator (iLQR), which ignores these second-order terms everywhere, on a co-design task for the Kinova arm, where we optimize the link lengths of the robot for a target reaching task. We show that optimizing using iLQR gradients diverges as ignoring the second-order dynamics affects the computation of the derivatives. Instead, optimizing using DDP gradients converges to the same optimum for a range of initial designs allowing our formulation to scale to complex systems.

Optimal Control via Combined Inference and Numerical Optimization

Derivative based optimization methods are efficient at solving optimal control problems near local optima. However, their ability to converge halts when derivative information vanishes. The inference approach to optimal control does not have strict requirements on the objective landscape. However, sampling, the primary tool for solving such problems, tends to be much slower in computation time. We propose a new method that combines second order methods with inference. We utilise the Kullback Leibler (KL) control framework to formulate an inference problem that computes the optimal controls from an adaptive distribution approximating the solution of the second order method. Our method allows for combining simple convex and non convex cost functions. This simplifies the process of cost function design and leverages the strengths of both inference and second order optimization. We compare our method to Model Predictive Path Integral (MPPI) and iterative Linear Quadratic Regulator (iLQG), outperforming both in sample efficiency and quality on manipulation and obstacle avoidance tasks.

Convex strategies for trajectory optimisation: application to the Polytope Traversal Problem

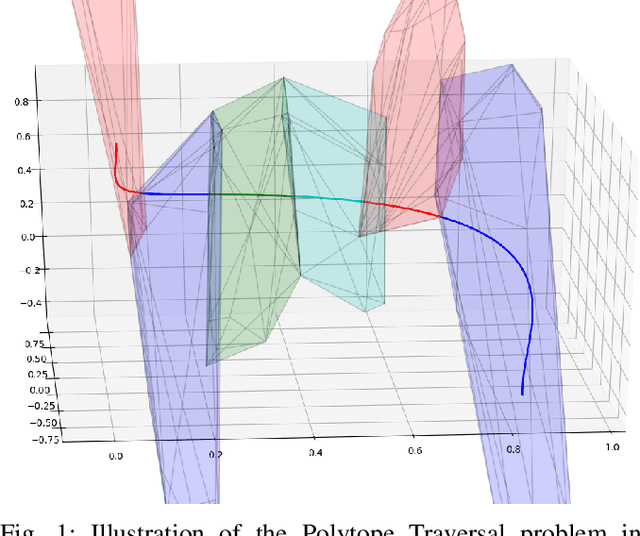
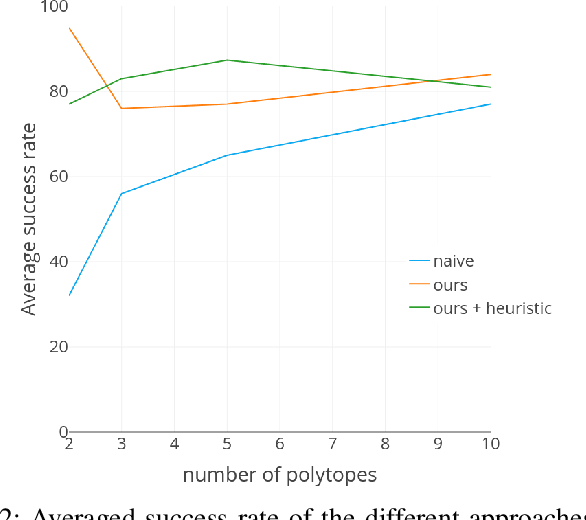
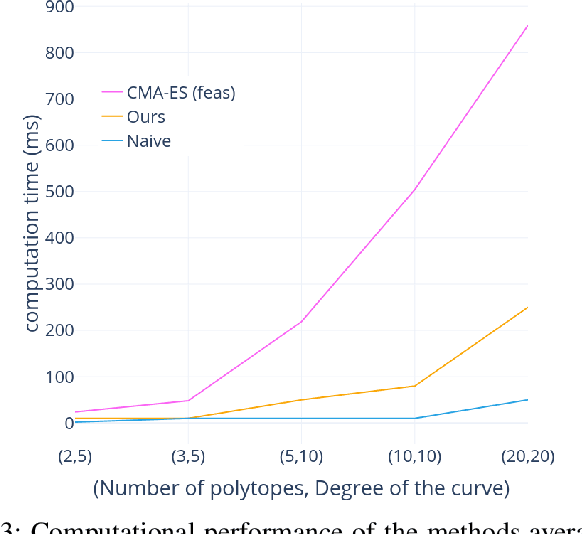
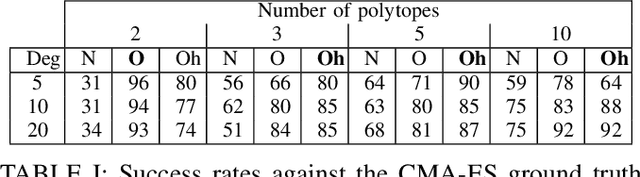
Non-linear Trajectory Optimisation (TO) methods require good initial guesses to converge to a locally optimal solution. A feasible guess can often be obtained by allocating a large amount of time for the trajectory to complete. However for unstable dynamical systems such as humanoid robots, this quasi-static assumption does not always hold. We propose a conservative formulation of the TO problem that simultaneously computes a feasible path and its time allocation. The problem is solved as an efficient convex optimisation problem guaranteed to converge to a locally optimal solution. The interest of the approach is illustrated with the computation of feasible trajectories that traverse sequentially a sequence of polytopes. We demonstrate that on instances of the problem where the quasi static solutions are not admissible, our approach is able to find a feasible solution with a success rate above $80 \%$ in all the scenarios considered, in less than 10ms for problems involving traversing less than 5 polytopes and less than 1s for problems involving 20 polytopes, thus demonstrating its ability to reliably provide initial guesses to advanced non linear solvers.