NAS: N-step computation of All Solutions to the footstep planning problem

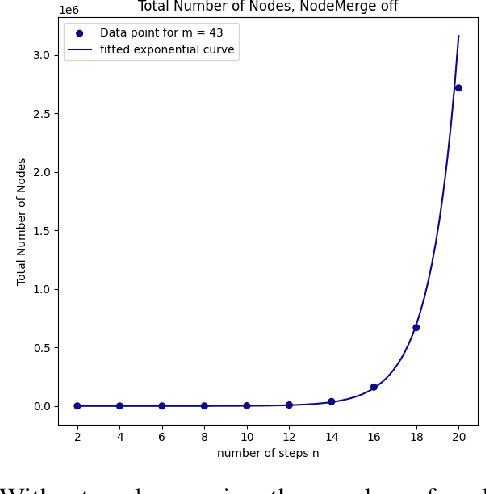
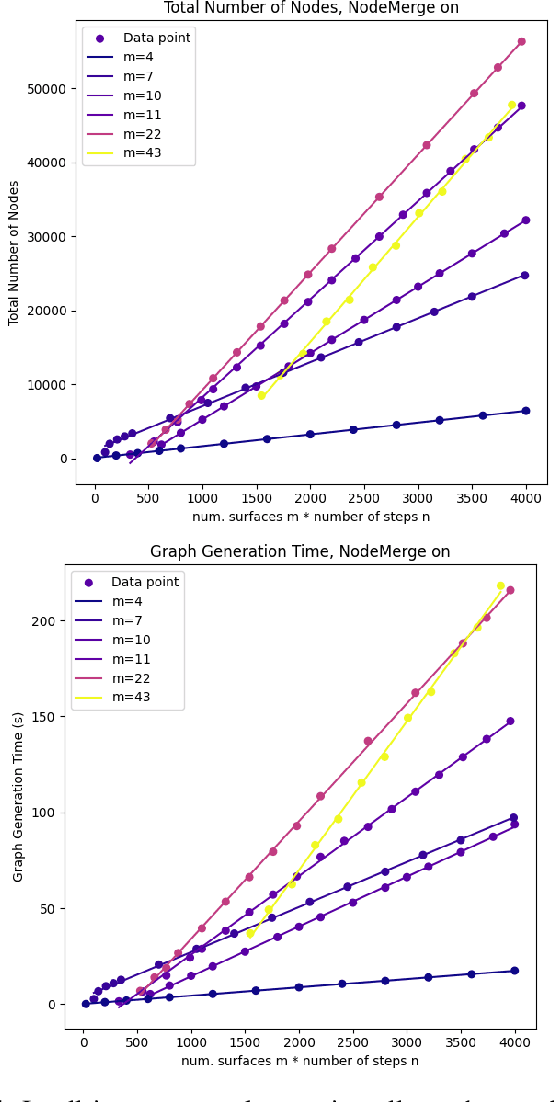
How many ways are there to climb a staircase in a given number of steps? Infinitely many, if we focus on the continuous aspect of the problem. A finite, possibly large number if we consider the discrete aspect, i.e. on which surface which effectors are going to step and in what order. We introduce NAS, an algorithm that considers both aspects simultaneously and computes all the possible solutions to such a contact planning problem, under standard assumptions. To our knowledge NAS is the first algorithm to produce a globally optimal policy, efficiently queried in real time for planning the next footsteps of a humanoid robot. Our empirical results (in simulation and on the Talos platform) demonstrate that, despite the theoretical exponential complexity, optimisations reduce the practical complexity of NAS to a manageable bilinear form, maintaining completeness guarantees and enabling efficient GPU parallelisation. NAS is demonstrated in a variety of scenarios for the Talos robot, both in simulation and on the hardware platform. Future work will focus on further reducing computation times and extending the algorithm's applicability beyond gaited locomotion. Our companion video is available at https://youtu.be/Shkf8PyDg4g

Solving Footstep Planning as a Feasibility Problem using L1-norm Minimization

One challenge of legged locomotion on uneven terrains is to deal with both the discrete problem of selecting a contact surface for each footstep and the continuous problem of placing each footstep on the selected surface. Consequently, footstep planning can be addressed with a Mixed Integer Program (MIP), an elegant but computationally-demanding method, which can make it unsuitable for online planning. We reformulate the MIP into a cardinality problem, then approximate it as a computationally efficient l1-norm minimisation, called SL1M. Moreover, we improve the performance and convergence of SL1M by combining it with a sampling-based root trajectory planner to prune irrelevant surface candidates. Our tests on the humanoid Talos in four representative scenarios show that SL1M always converges faster than MIP. For scenarios when the combinatorial complexity is small (< 10 surfaces per step), SL1M converges at least two times faster than MIP with no need for pruning. In more complex cases, SL1M converges up to 100 times faster than MIP with the help of pruning. Moreover, pruning can also improve the MIP computation time. The versatility of the framework is shown with additional tests on the quadruped robot ANYmal.

Learning How to Walk: Warm-starting Optimal Control Solver with Memory of Motion

In this paper, we propose a framework to build a memory of motion for warm-starting an optimal control solver for the locomotion task of a humanoid robot. We use HPP Loco3D, a versatile locomotion planner, to generate offline a set of dynamically consistent whole-body trajectory to be stored as the memory of motion. The learning problem is formulated as a regression problem to predict a single-step motion given the desired contact locations, which is used as a building block for producing multi-step motions. The predicted motion is then used as a warm-start for the fast optimal control solver Crocoddyl. We have shown that the approach manages to reduce the required number of iterations to reach the convergence from $\sim$9.5 to only $\sim$3.0 iterations for the single-step motion and from $\sim$6.2 to $\sim$4.5 iterations for the multi-step motion, while maintaining the solution's quality.

SL1M: Sparse L1-norm Minimization for contact planning on uneven terrain

One of the main challenges of planning legged locomotion in complex environments is the combinatorial contact selection problem. Recent contributions propose to use integer variables to represent which contact surface is selected, and then to rely on modern mixed-integer (MI) optimization solvers to handle this combinatorial issue. To reduce the computational cost of MI, we exploit the sparsity properties of L1 norm minimization techniques to relax the contact planning problem into a feasibility linear program. Our approach accounts for kinematic reachability of the center of mass (COM) and of the contact effectors. We ensure the existence of a quasi-static COM trajectory by restricting our plan to quasi-flat contacts. For planning 10 steps with less than 10 potential contact surfaces for each phase, our approach is 50 to 100 times faster that its MI counterpart, which suggests potential applications for online contact re-planning. The method is demonstrated in simulation with the humanoid robots HRP-2 and Talos over various scenarios.

Contact Planning for the ANYmal Quadruped Robot using an Acyclic Reachability-Based Planner

Despite the great progress in quadrupedal robotics during the last decade, selecting good contacts (footholds) in highly uneven and cluttered environments still remains an open challenge. This paper builds upon a state-of-the-art approach, already successfully used for humanoid robots, and applies it to our robotic platform; the quadruped robot ANY-mal. The proposed algorithm decouples the problem into two subprob-lems: first a guide trajectory for the robot is generated, then contacts are created along this trajectory. Both subproblems rely on approximations and heuristics that need to be tuned. The main contribution of this work is to explain how this algorithm has been retuned to work with ANY-mal and to show the relevance of the approach with a variety of tests in realistic dynamic simulations.