Reinforcement Learning from Wild Animal Videos

We propose to learn legged robot locomotion skills by watching thousands of wild animal videos from the internet, such as those featured in nature documentaries. Indeed, such videos offer a rich and diverse collection of plausible motion examples, which could inform how robots should move. To achieve this, we introduce Reinforcement Learning from Wild Animal Videos (RLWAV), a method to ground these motions into physical robots. We first train a video classifier on a large-scale animal video dataset to recognize actions from RGB clips of animals in their natural habitats. We then train a multi-skill policy to control a robot in a physics simulator, using the classification score of a third-person camera capturing videos of the robot's movements as a reward for reinforcement learning. Finally, we directly transfer the learned policy to a real quadruped Solo. Remarkably, despite the extreme gap in both domain and embodiment between animals in the wild and robots, our approach enables the policy to learn diverse skills such as walking, jumping, and keeping still, without relying on reference trajectories nor skill-specific rewards.

Whole-body MPC and sensitivity analysis of a real time foot step sequencer for a biped robot Bolt

This paper presents a novel controller for the bipedal robot Bolt. Our approach leverages a whole-body model predictive controller in conjunction with a footstep sequencer to achieve robust locomotion. Simulation results demonstrate effective velocity tracking as well as push and slippage recovery abilities. In addition to that, we provide a theoretical sensitivity analysis of the footstep sequencing problem to enhance the understanding of the results.

NAS: N-step computation of All Solutions to the footstep planning problem

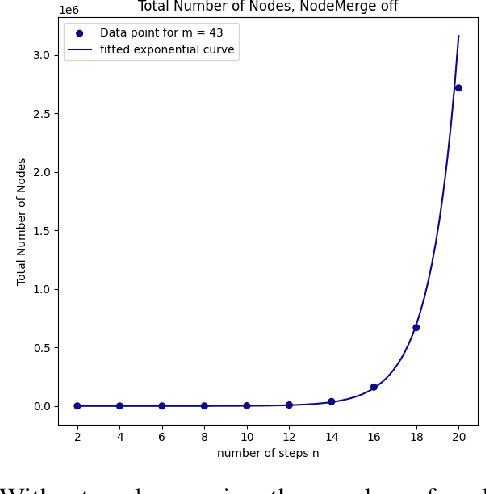
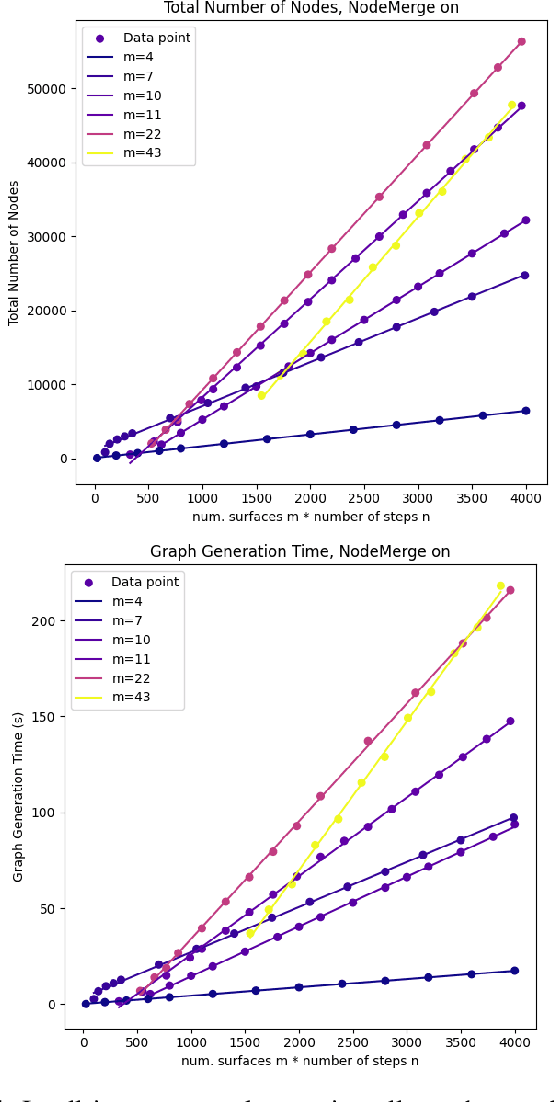
How many ways are there to climb a staircase in a given number of steps? Infinitely many, if we focus on the continuous aspect of the problem. A finite, possibly large number if we consider the discrete aspect, i.e. on which surface which effectors are going to step and in what order. We introduce NAS, an algorithm that considers both aspects simultaneously and computes all the possible solutions to such a contact planning problem, under standard assumptions. To our knowledge NAS is the first algorithm to produce a globally optimal policy, efficiently queried in real time for planning the next footsteps of a humanoid robot. Our empirical results (in simulation and on the Talos platform) demonstrate that, despite the theoretical exponential complexity, optimisations reduce the practical complexity of NAS to a manageable bilinear form, maintaining completeness guarantees and enabling efficient GPU parallelisation. NAS is demonstrated in a variety of scenarios for the Talos robot, both in simulation and on the hardware platform. Future work will focus on further reducing computation times and extending the algorithm's applicability beyond gaited locomotion. Our companion video is available at https://youtu.be/Shkf8PyDg4g

CaT: Constraints as Terminations for Legged Locomotion Reinforcement Learning

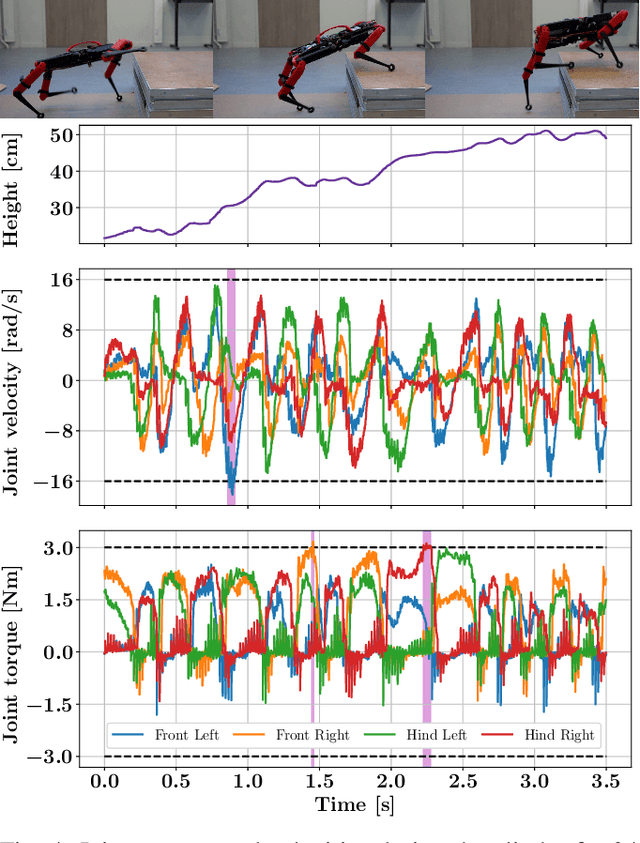
Deep Reinforcement Learning (RL) has demonstrated impressive results in solving complex robotic tasks such as quadruped locomotion. Yet, current solvers fail to produce efficient policies respecting hard constraints. In this work, we advocate for integrating constraints into robot learning and present Constraints as Terminations (CaT), a novel constrained RL algorithm. Departing from classical constrained RL formulations, we reformulate constraints through stochastic terminations during policy learning: any violation of a constraint triggers a probability of terminating potential future rewards the RL agent could attain. We propose an algorithmic approach to this formulation, by minimally modifying widely used off-the-shelf RL algorithms in robot learning (such as Proximal Policy Optimization). Our approach leads to excellent constraint adherence without introducing undue complexity and computational overhead, thus mitigating barriers to broader adoption. Through empirical evaluation on the real quadruped robot Solo crossing challenging obstacles, we demonstrate that CaT provides a compelling solution for incorporating constraints into RL frameworks. Videos and code are available at https://constraints-as-terminations.github.io.

Design, analysis and control of the series-parallel hybrid RH5 humanoid robot

Last decades of humanoid research has shown that humanoids developed for high dynamic performance require a stiff structure and optimal distribution of mass--inertial properties. Humanoid robots built with a purely tree type architecture tend to be bulky and usually suffer from velocity and force/torque limitations. This paper presents a novel series-parallel hybrid humanoid called RH5 which is 2 m tall and weighs only 62.5 kg capable of performing heavy-duty dynamic tasks with 5 kg payloads in each hand. The analysis and control of this humanoid is performed with whole-body trajectory optimization technique based on differential dynamic programming (DDP). Additionally, we present an improved contact stability soft-constrained DDP algorithm which is able to generate physically consistent walking trajectories for the humanoid that can be tracked via a simple PD position control in a physics simulator. Finally, we showcase preliminary experimental results on the RH5 humanoid robot.

Motion Planning in Irreducible Path Spaces

The motion of a mechanical system can be defined as a path through its configuration space. Computing such a path has a computational complexity scaling exponentially with the dimensionality of the configuration space. We propose to reduce the dimensionality of the configuration space by introducing the irreducible path --- a path having a minimal swept volume. The paper consists of three parts: In part I, we define the space of all irreducible paths and show that planning a path in the irreducible path space preserves completeness of any motion planning algorithm. In part II, we construct an approximation to the irreducible path space of a serial kinematic chain under certain assumptions. In part III, we conduct motion planning using the irreducible path space for a mechanical snake in a turbine environment, for a mechanical octopus with eight arms in a pipe system and for the sideways motion of a humanoid robot moving through a room with doors and through a hole in a wall. We demonstrate that the concept of an irreducible path can be applied to any motion planning algorithm taking curvature constraints into account.

How do walkers avoid a mobile robot crossing their way?

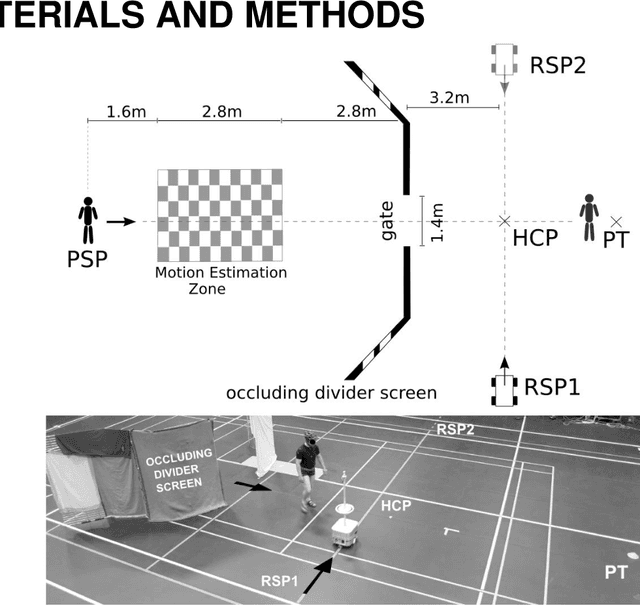
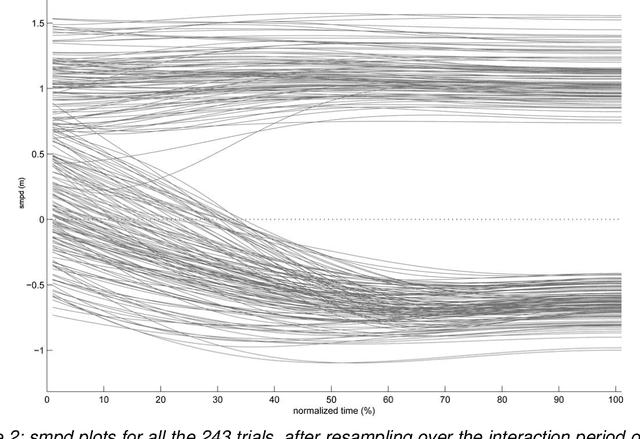
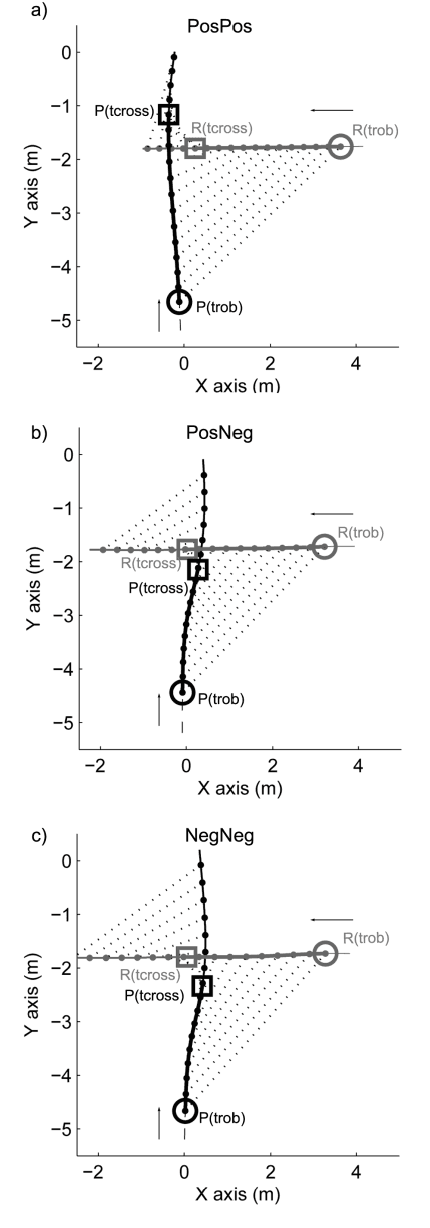
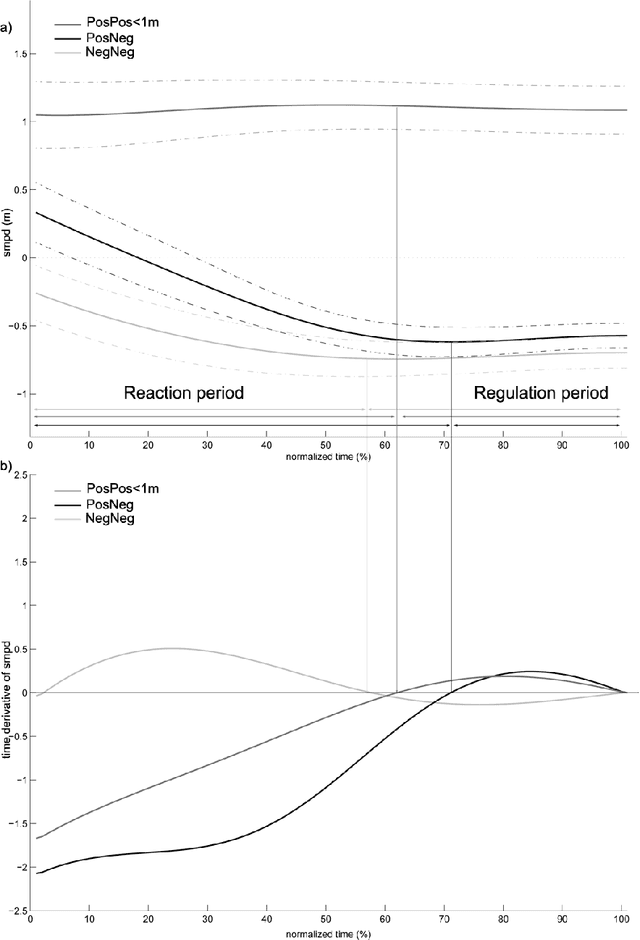
Robots and Humans have to share the same environment more and more often. In the aim of steering robots in a safe and convenient manner among humans it is required to understand how humans interact with them. This work focuses on collision avoidance between a human and a robot during locomotion. Having in mind previous results on human obstacle avoidance, as well as the description of the main principles which guide collision avoidance strategies, we observe how humans adapt a goal-directed locomotion task when they have to interfere with a mobile robot. Our results show differences in the strategy set by humans to avoid a robot in comparison with avoiding another human. Humans prefer to give the way to the robot even when they are likely to pass first at the beginning of the interaction.