An Efficient Representation of Whole-body Model Predictive Control for Online Compliant Dual-arm Mobile Manipulation

Dual-arm mobile manipulators can transport and manipulate large-size objects with simple end-effectors. To interact with dynamic environments with strict safety and compliance requirements, achieving whole-body motion planning online while meeting various hard constraints for such highly redundant mobile manipulators poses a significant challenge. We tackle this challenge by presenting an efficient representation of whole-body motion trajectories within our bilevel model-based predictive control (MPC) framework. We utilize B\'ezier-curve parameterization to represent the optimized collision-free trajectories of two collaborating end-effectors in the first MPC, facilitating fast long-horizon object-oriented motion planning in SE(3) while considering approximated feasibility constraints. This approach is further applied to parameterize whole-body trajectories in the second MPC for whole-body motion generation with predictive admittance control in a relatively short horizon while satisfying whole-body hard constraints. This representation enables two MPCs with continuous properties, thereby avoiding inaccurate model-state transition and dense decision-variable settings in existing MPCs using the discretization method. It strengthens the online execution of the bilevel MPC framework in high-dimensional space and facilitates the generation of consistent commands for our hybrid position/velocity-controlled robot. The simulation comparisons and real-world experiments demonstrate the efficiency and robustness of this approach in various scenarios for static and dynamic obstacle avoidance, and compliant interaction control with the manipulated object and external disturbances.

NAS: N-step computation of All Solutions to the footstep planning problem

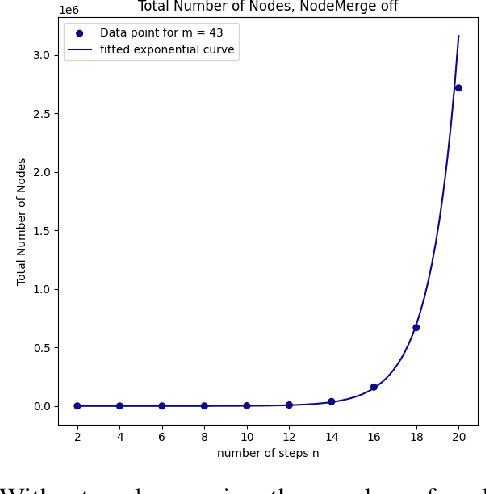
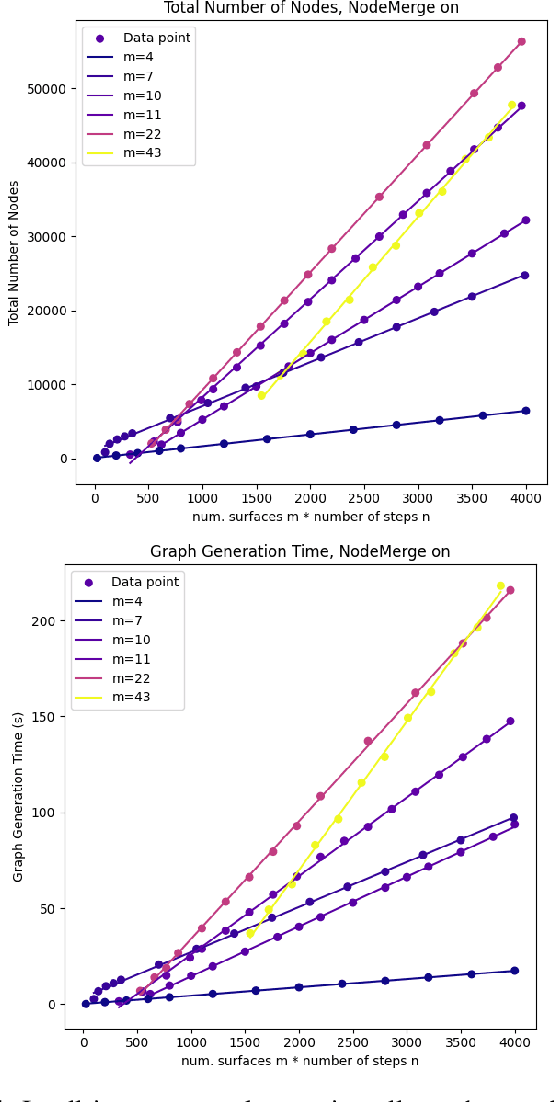
How many ways are there to climb a staircase in a given number of steps? Infinitely many, if we focus on the continuous aspect of the problem. A finite, possibly large number if we consider the discrete aspect, i.e. on which surface which effectors are going to step and in what order. We introduce NAS, an algorithm that considers both aspects simultaneously and computes all the possible solutions to such a contact planning problem, under standard assumptions. To our knowledge NAS is the first algorithm to produce a globally optimal policy, efficiently queried in real time for planning the next footsteps of a humanoid robot. Our empirical results (in simulation and on the Talos platform) demonstrate that, despite the theoretical exponential complexity, optimisations reduce the practical complexity of NAS to a manageable bilinear form, maintaining completeness guarantees and enabling efficient GPU parallelisation. NAS is demonstrated in a variety of scenarios for the Talos robot, both in simulation and on the hardware platform. Future work will focus on further reducing computation times and extending the algorithm's applicability beyond gaited locomotion. Our companion video is available at https://youtu.be/Shkf8PyDg4g

Online Multi-Contact Receding Horizon Planning via Value Function Approximation

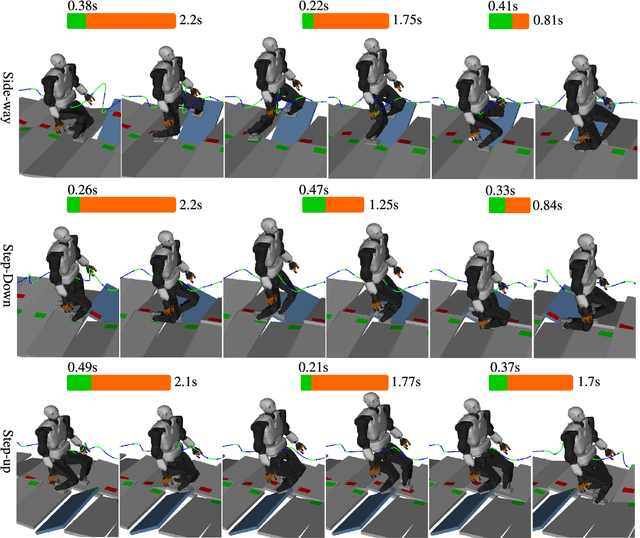
Planning multi-contact motions in a receding horizon fashion requires a value function to guide the planning with respect to the future, e.g., building momentum to traverse large obstacles. Traditionally, the value function is approximated by computing trajectories in a prediction horizon (never executed) that foresees the future beyond the execution horizon. However, given the non-convex dynamics of multi-contact motions, this approach is computationally expensive. To enable online Receding Horizon Planning (RHP) of multi-contact motions, we find efficient approximations of the value function. Specifically, we propose a trajectory-based and a learning-based approach. In the former, namely RHP with Multiple Levels of Model Fidelity, we approximate the value function by computing the prediction horizon with a convex relaxed model. In the latter, namely Locally-Guided RHP, we learn an oracle to predict local objectives for locomotion tasks, and we use these local objectives to construct local value functions for guiding a short-horizon RHP. We evaluate both approaches in simulation by planning centroidal trajectories of a humanoid robot walking on moderate slopes, and on large slopes where the robot cannot maintain static balance. Our results show that locally-guided RHP achieves the best computation efficiency (95\%-98.6\% cycles converge online). This computation advantage enables us to demonstrate online receding horizon planning of our real-world humanoid robot Talos walking in dynamic environments that change on-the-fly.

Control of Humanoid in Multiple Fixed and Moving Unilateral Contacts

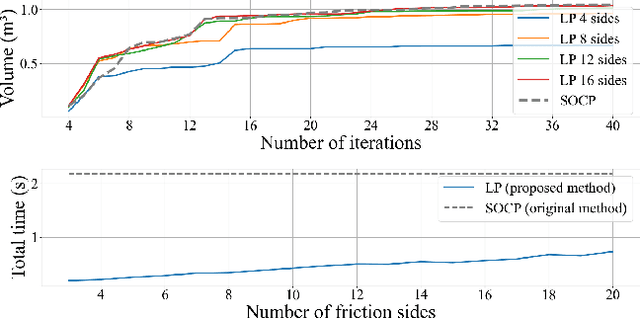
Enforcing balance of multi-limbed robots in multiple non-coplanar unilateral contact settings is challenging when a subset of such contacts are also induced in motion tasks. The first contribution of this paper is in enhancing the computational performance of state-of-the-art geometric center-of-mass inclusion-based balance method to be integrated online as part of a task-space whole-body control framework. As a consequence, our second contribution lies in integrating such a balance region with relevant contact force distribution without pre-computing a target center-of-mass. This last feature is essential to leave the latter with freedom to better comply with other existing tasks that are not captured in classical twolevel approaches. We assess the performance of our proposed method through experiments using the HRP-4 humanoid robot.

Humanoid Control Under Interchangeable Fixed and Sliding Unilateral Contacts

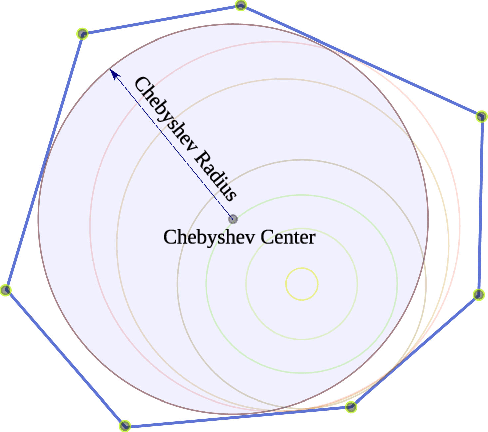
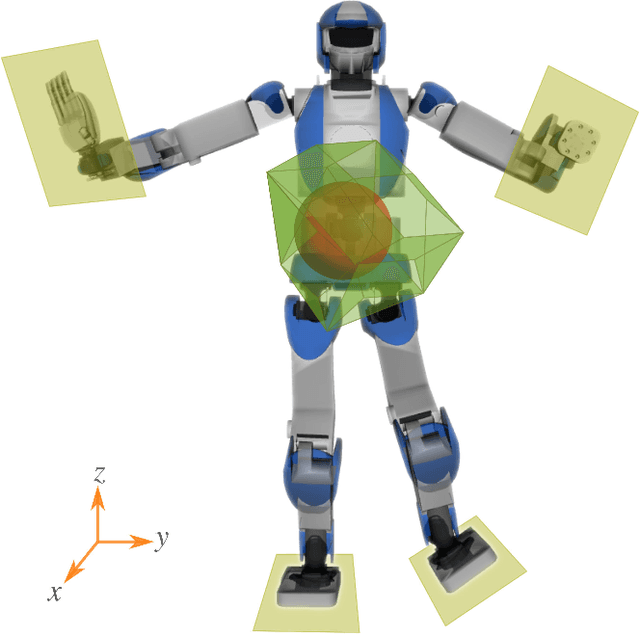
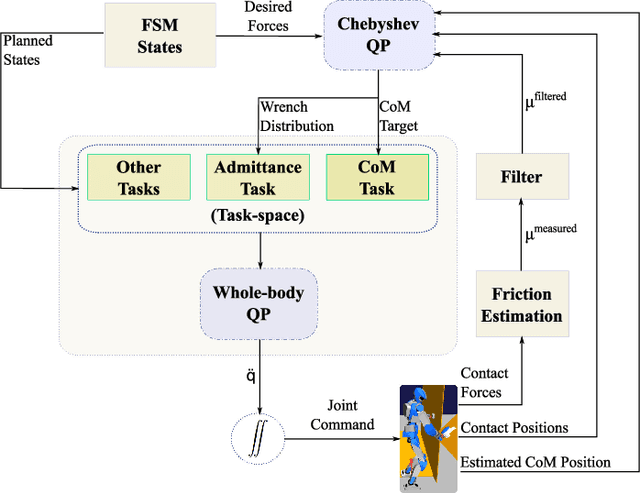
In this letter, we propose a whole-body control strategy for humanoid robots in multi-contact settings that enables switching between fixed and sliding contacts under active balance. We compute, in real-time, a safe center-of-mass position and wrench distribution of the contact points based on the Chebyshev center. Our solution is formulated as a quadratic programming problem without a priori computation of balance regions. We assess our approach with experiments highlighting switches between fixed and sliding contact modes in multi-contact configurations. A humanoid robot demonstrates such contact interchanges from fully-fixed to multi-sliding and also shuffling of the foot. The scenarios illustrate the performance of our control scheme in achieving the desired forces, CoM position attractor, and planned trajectories while actively maintaining balance.

Balance of Humanoid robot in Multi-contact and Sliding Scenarios

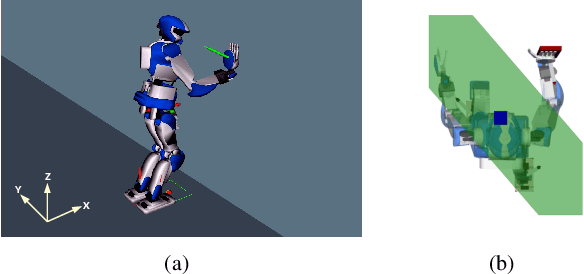
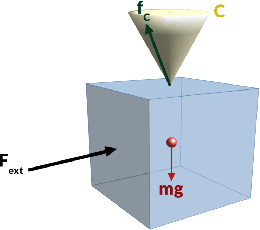
This study deals with the balance of humanoid or multi-legged robots in a multi-contact setting where a chosen subset of contacts is undergoing desired sliding-task motions. One method to keep balance is to hold the center-of-mass (CoM) within an admissible convex area. This area should be calculated based on the contact positions and forces. We introduce a methodology to compute this CoM support area (CSA) for multiple fixed and sliding contacts. To select the most appropriate CoM position inside CSA, we account for (i) constraints of multiple fixed and sliding contacts, (ii) desired wrench distribution for contacts, and (iii) desired position of CoM (eventually dictated by other tasks). These are formulated as a quadratic programming optimization problem. We illustrate our approach with pushing against a wall and wiping and conducted experiments using the HRP-4 humanoid robot.