ALPINE: a climbing robot for operations in mountain environments

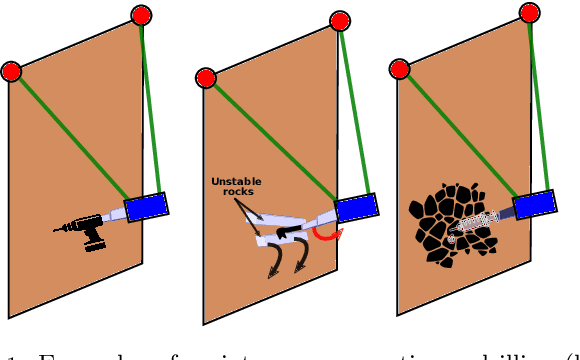
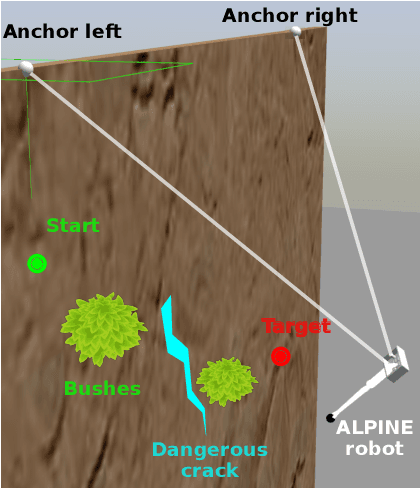
Mountain slopes are perfect examples of harsh environments in which humans are required to perform difficult and dangerous operations such as removing unstable boulders, dangerous vegetation or deploying safety nets. A good replacement for human intervention can be offered by climbing robots. The different solutions existing in the literature are not up to the task for the difficulty of the requirements (navigation, heavy payloads, flexibility in the execution of the tasks). In this paper, we propose a robotic platform that can fill this gap. Our solution is based on a robot that hangs on ropes, and uses a retractable leg to jump away from the mountain walls. Our package of mechanical solutions, along with the algorithms developed for motion planning and control, delivers swift navigation on irregular and steep slopes, the possibility to overcome or travel around significant natural barriers, and the ability to carry heavy payloads and execute complex tasks. In the paper, we give a full account of our main design and algorithmic choices and show the feasibility of the solution through a large number of physically simulated scenarios.

CACTO-SL: Using Sobolev Learning to improve Continuous Actor-Critic with Trajectory Optimization

Trajectory Optimization (TO) and Reinforcement Learning (RL) are powerful and complementary tools to solve optimal control problems. On the one hand, TO can efficiently compute locally-optimal solutions, but it tends to get stuck in local minima if the problem is not convex. On the other hand, RL is typically less sensitive to non-convexity, but it requires a much higher computational effort. Recently, we have proposed CACTO (Continuous Actor-Critic with Trajectory Optimization), an algorithm that uses TO to guide the exploration of an actor-critic RL algorithm. In turns, the policy encoded by the actor is used to warm-start TO, closing the loop between TO and RL. In this work, we present an extension of CACTO exploiting the idea of Sobolev learning. To make the training of the critic network faster and more data efficient, we enrich it with the gradient of the Value function, computed via a backward pass of the differential dynamic programming algorithm. Our results show that the new algorithm is more efficient than the original CACTO, reducing the number of TO episodes by a factor ranging from 3 to 10, and consequently the computation time. Moreover, we show that CACTO-SL helps TO to find better minima and to produce more consistent results.

Efficient Reinforcement Learning for Jumping Monopods

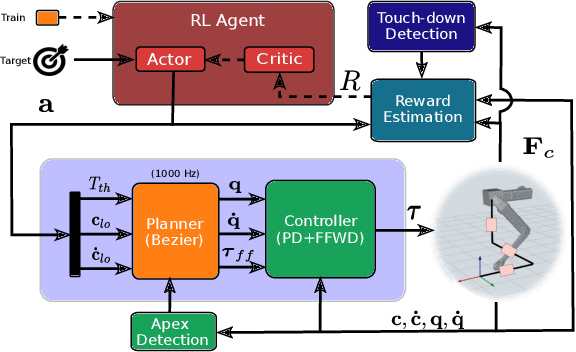
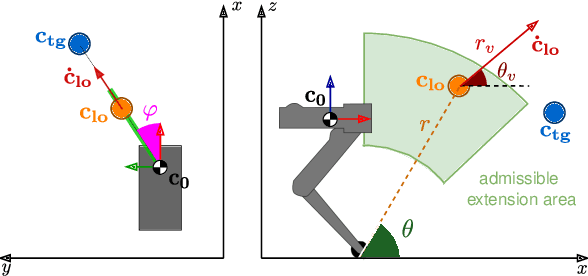
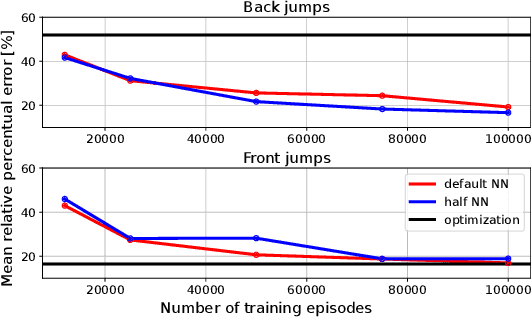
In this work, we consider the complex control problem of making a monopod reach a target with a jump. The monopod can jump in any direction and the terrain underneath its foot can be uneven. This is a template of a much larger class of problems, which are extremely challenging and computationally expensive to solve using standard optimisation-based techniques. Reinforcement Learning (RL) could be an interesting alternative, but the application of an end-to-end approach in which the controller must learn everything from scratch, is impractical. The solution advocated in this paper is to guide the learning process within an RL framework by injecting physical knowledge. This expedient brings to widespread benefits, such as a drastic reduction of the learning time, and the ability to learn and compensate for possible errors in the low-level controller executing the motion. We demonstrate the advantage of our approach with respect to both optimization-based and end-to-end RL approaches.

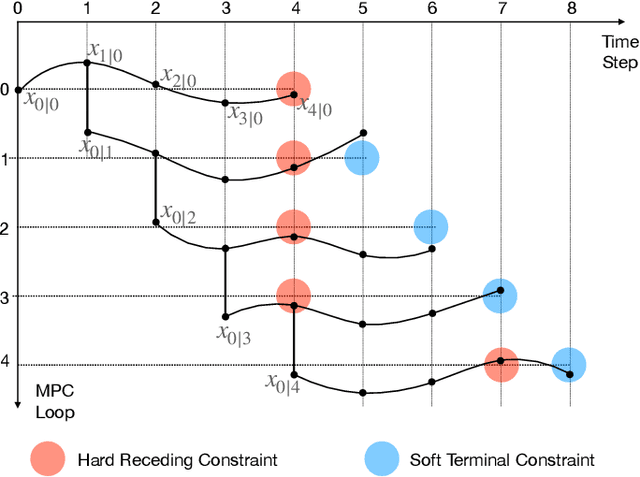
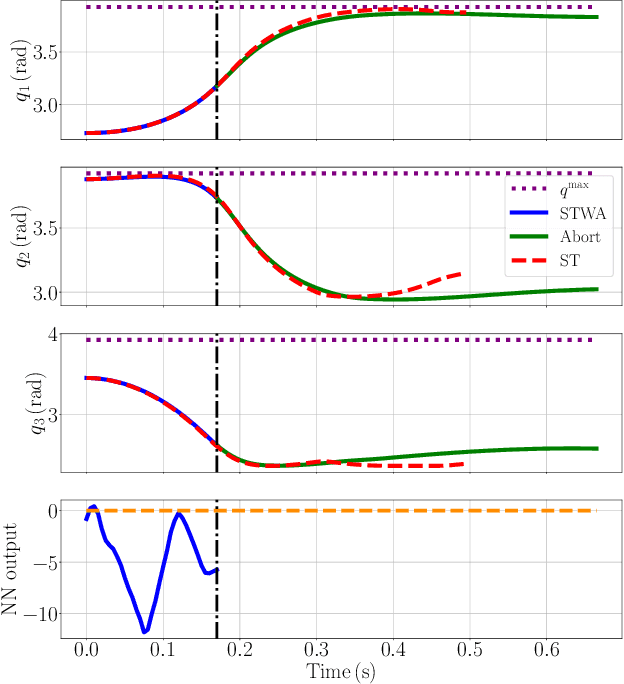
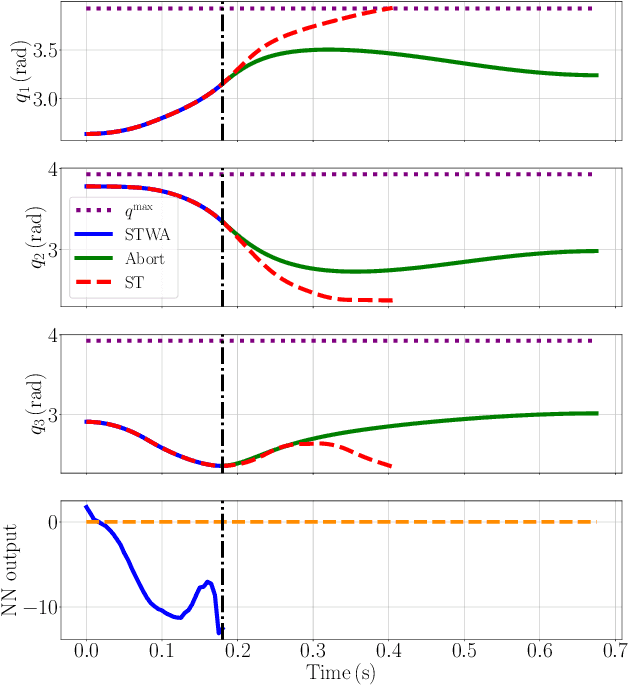
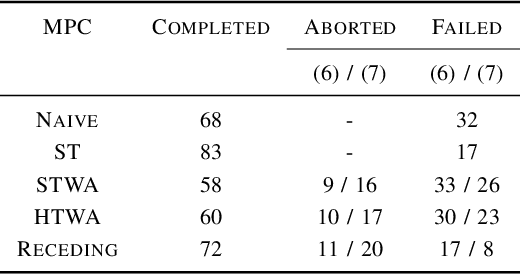
Receding-Constraint Model Predictive Control using a Learned Approximate Control-Invariant Set

In recent years, advanced model-based and data-driven control methods are unlocking the potential of complex robotics systems, and we can expect this trend to continue at an exponential rate in the near future. However, ensuring safety with these advanced control methods remains a challenge. A well-known tool to make controllers (either Model Predictive Controllers or Reinforcement Learning policies) safe, is the so-called control-invariant set (a.k.a. safe set). Unfortunately, for nonlinear systems, such a set cannot be exactly computed in general. Numerical algorithms exist for computing approximate control-invariant sets, but classic theoretic control methods break down if the set is not exact. This paper presents our recent efforts to address this issue. We present a novel Model Predictive Control scheme that can guarantee recursive feasibility and/or safety under weaker assumptions than classic methods. In particular, recursive feasibility is guaranteed by making the safe-set constraint move backward over the horizon, and assuming that such set satisfies a condition that is weaker than control invariance. Safety is instead guaranteed under an even weaker assumption on the safe set, triggering a safe task-abortion strategy whenever a risk of constraint violation is detected. We evaluated our approach on a simulated robot manipulator, empirically demonstrating that it leads to less constraint violations than state-of-the-art approaches, while retaining reasonable performance in terms of tracking cost and number of completed tasks.

Multi-contact Stochastic Predictive Control for Legged Robots with Contact Locations Uncertainty

Trajectory optimization under uncertainties is a challenging problem for robots in contact with the environment. Such uncertainties are inevitable due to estimation errors, control imperfections, and model mismatches between planning models used for control and the real robot dynamics. This induces control policies that could violate the contact location constraints by making contact at unintended locations, and as a consequence leading to unsafe motion plans. This work addresses the problem of robust kino-dynamic whole-body trajectory optimization using stochastic nonlinear model predictive control (SNMPC) by considering additive uncertainties on the model dynamics subject to contact location chance-constraints as a function of robot's full kinematics. We demonstrate the benefit of using SNMPC over classic nonlinear MPC (NMPC) for whole-body trajectory optimization in terms of contact location constraint satisfaction (safety). We run extensive Monte-Carlo simulations for a quadruped robot performing agile trotting and bounding motions over small stepping stones, where contact location satisfaction becomes critical. Our results show that SNMPC is able to perform all motions safely with 100% success rate, while NMPC failed 48.3% of all motions.

Reactive Landing Controller for Quadruped Robots

Quadruped robots are machines intended for challenging and harsh environments. Despite the progress in locomotion strategy, safely recovering from unexpected falls or planned drops is still an open problem. It is further made more difficult when high horizontal velocities are involved. In this work, we propose an optimization-based reactive Landing Controller that uses only proprioceptive measures for torque-controlled quadruped robots that free-fall on a flat horizontal ground, knowing neither the distance to the landing surface nor the flight time. Based on an estimate of the Center of Mass horizontal velocity, the method uses the Variable Height Springy Inverted Pendulum model for continuously recomputing the feet position while the robot is falling. In this way, the quadruped is ready to attain a successful landing in all directions, even in the presence of significant horizontal velocities. The method is demonstrated to dramatically enlarge the region of horizontal velocities that can be dealt with by a naive approach that keeps the feet still during the airborne stage. To the best of our knowledge, this is the first time that a quadruped robot can successfully recover from falls with horizontal velocities up to 3 m/s in simulation. Experiments prove that the used platform, Go1, can successfully attain a stable standing configuration from falls with various horizontal velocity and different angular perturbations.

VBOC: Learning the Viability Boundary of a Robot Manipulator using Optimal Control

Safety is often the most important requirement in robotics applications. Nonetheless, control techniques that can provide safety guarantees are still extremely rare for nonlinear systems, such as robot manipulators. A well-known tool to ensure safety is the Viability kernel, which is the largest set of states from which safety can be ensured. Unfortunately, computing such a set for a nonlinear system is extremely challenging in general. Several numerical algorithms for approximating it have been proposed in the literature, but they suffer from the curse of dimensionality. This paper presents a new approach for numerically approximating the viability kernel of robot manipulators. Our approach solves optimal control problems to compute states that are guaranteed to be on the boundary of the set. This allows us to learn directly the set boundary, therefore learning in a smaller dimensional space. Compared to the state of the art on systems up to dimension 6, our algorithm resulted to be more than 2 times as accurate for the same computation time, or 6 times as fast to reach the same accuracy.

Optimization-Based Control for Dynamic Legged Robots

In a world designed for legs, quadrupeds, bipeds, and humanoids have the opportunity to impact emerging robotics applications from logistics, to agriculture, to home assistance. The goal of this survey is to cover the recent progress toward these applications that has been driven by model-based optimization for the real-time generation and control of movement. The majority of the research community has converged on the idea of generating locomotion control laws by solving an optimal control problem (OCP) in either a model-based or data-driven manner. However, solving the most general of these problems online remains intractable due to complexities from intermittent unidirectional contacts with the environment, and from the many degrees of freedom of legged robots. This survey covers methods that have been pursued to make these OCPs computationally tractable, with specific focus on how environmental contacts are treated, how the model can be simplified, and how these choices affect the numerical solution methods employed. The survey focuses on model-based optimization, covering its recent use in a stand alone fashion, and suggesting avenues for combination with learning-based formulations to further accelerate progress in this growing field.

CACTO: Continuous Actor-Critic with Trajectory Optimization -- Towards global optimality

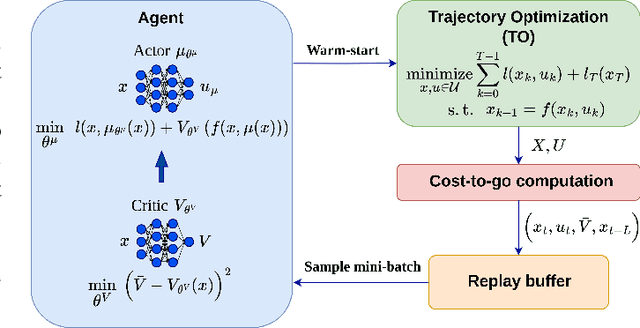
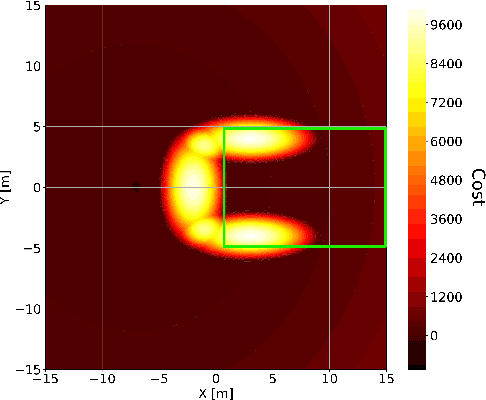
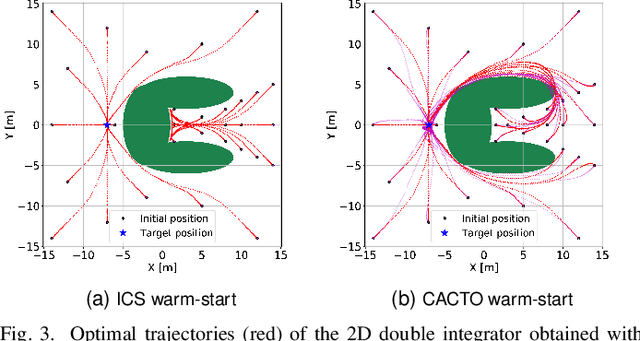
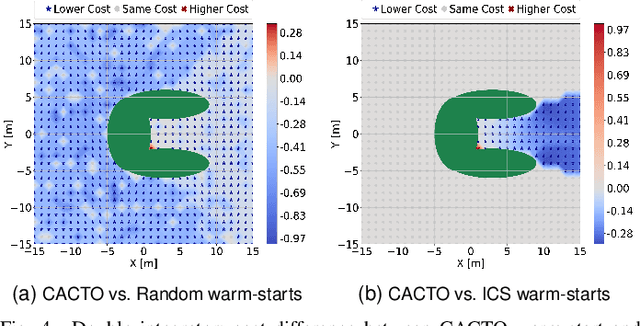
This paper presents a novel algorithm for the continuous control of dynamical systems that combines Trajectory Optimization (TO) and Reinforcement Learning (RL) in a single framework. The motivations behind this algorithm are the two main limitations of TO and RL when applied to continuous nonlinear systems to minimize a non-convex cost function. Specifically, TO can get stuck in poor local minima when the search is not initialized close to a ``good'' minimum. On the other hand, when dealing with continuous state and control spaces, the RL training process may be excessively long and strongly dependent on the exploration strategy. Thus, our algorithm learns a ``good'' control policy via TO-guided RL policy search that, when used as initial guess provider for TO, makes the trajectory optimization process less prone to converge to poor local optima. Our method is validated on several reaching problems featuring non-convex obstacle avoidance with different dynamical systems, including a car model with 6d state, and a 3-joint planar manipulator. Our results show the great capabilities of CACTO in escaping local minima, while being more computationally efficient than the DDPG RL algorithm.