Multi-contact Stochastic Predictive Control for Legged Robots with Contact Locations Uncertainty

Trajectory optimization under uncertainties is a challenging problem for robots in contact with the environment. Such uncertainties are inevitable due to estimation errors, control imperfections, and model mismatches between planning models used for control and the real robot dynamics. This induces control policies that could violate the contact location constraints by making contact at unintended locations, and as a consequence leading to unsafe motion plans. This work addresses the problem of robust kino-dynamic whole-body trajectory optimization using stochastic nonlinear model predictive control (SNMPC) by considering additive uncertainties on the model dynamics subject to contact location chance-constraints as a function of robot's full kinematics. We demonstrate the benefit of using SNMPC over classic nonlinear MPC (NMPC) for whole-body trajectory optimization in terms of contact location constraint satisfaction (safety). We run extensive Monte-Carlo simulations for a quadruped robot performing agile trotting and bounding motions over small stepping stones, where contact location satisfaction becomes critical. Our results show that SNMPC is able to perform all motions safely with 100% success rate, while NMPC failed 48.3% of all motions.

Nonlinear Stochastic Trajectory Optimization for Centroidal Momentum Motion Generation of Legged Robots

Generation of robust trajectories for legged robots remains a challenging task due to the underlying nonlinear, hybrid and intrinsically unstable dynamics which needs to be stabilized through limited contact forces. Furthermore, disturbances arising from unmodelled contact interactions with the environment and model mismatches can hinder the quality of the planned trajectories leading to unsafe motions. In this work, we propose to use stochastic trajectory optimization for generating robust centroidal momentum trajectories to account for additive uncertainties on the model dynamics and parametric uncertainties on contact locations. Through an alternation between the robust centroidal and whole-body trajectory optimizations, we generate robust momentum trajectories while being consistent with the whole-body dynamics. We perform an extensive set of simulations subject to different uncertainties on a quadruped robot showing that our stochastic trajectory optimization problem reduces the amount of foot slippage for different gaits while achieving better performance over deterministic planning.

On the Use of Torque Measurement in Centroidal State Estimation

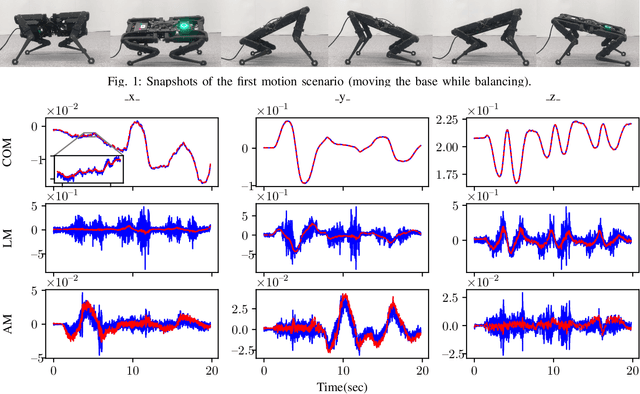
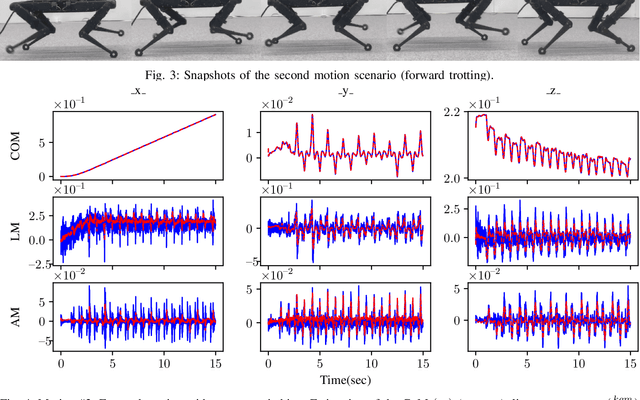
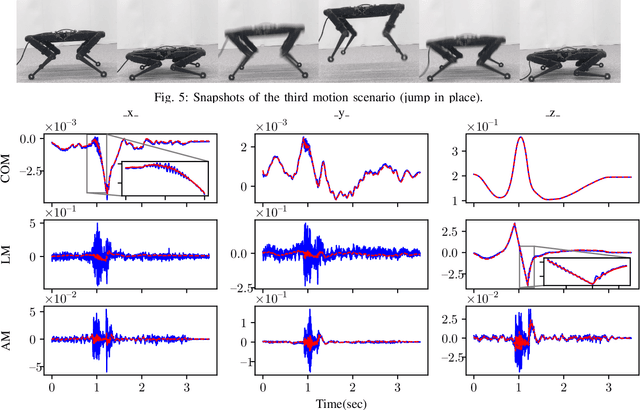
State of the art legged robots are either capable of measuring torque at the output of their drive systems, or have transparent drive systems which enable the computation of joint torques from motor currents. In either case, this sensor modality is seldom used in state estimation. In this paper, we propose to use joint torque measurements to estimate the centroidal states of legged robots. To do so, we project the whole-body dynamics of a legged robot into the nullspace of the contact constraints, allowing expression of the dynamics independent of the contact forces. Using the constrained dynamics and the centroidal momentum matrix, we are able to directly relate joint torques and centroidal states dynamics. Using the resulting model as the process model of an Extended Kalman Filter (EKF), we fuse the torque measurement in the centroidal state estimation problem. Through real-world experiments on a quadruped robot with different gaits, we demonstrate that the estimated centroidal states from our torque-based EKF drastically improve the estimation of these quantities compared to direct computation.

Stochastic and Robust MPC for Bipedal Locomotion: A Comparative Study on Robustness and Performance

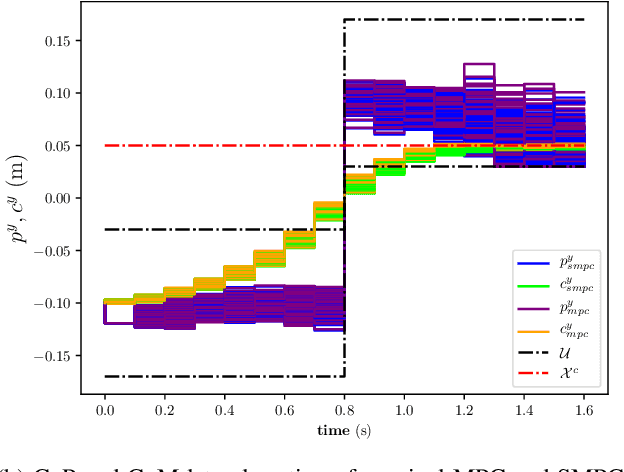
Linear Model Predictive Control (MPC) has been successfully used for generating feasible walking motions for humanoid robots. However, the effect of uncertainties on constraints satisfaction has only been studied using Robust MPC (RMPC) approaches, which account for the worst-case realization of bounded disturbances at each time instant. In this letter, we propose for the first time to use linear stochastic MPC (SMPC) to account for uncertainties in bipedal walking. We show that SMPC offers more flexibility to the user (or a high level decision maker) by tolerating small (user-defined) probabilities of constraint violation. Therefore, SMPC can be tuned to achieve a constraint satisfaction probability that is arbitrarily close to 100\%, but without sacrificing performance as much as tube-based RMPC. We compare SMPC against RMPC in terms of robustness (constraint satisfaction) and performance (optimality). Our results highlight the benefits of SMPC and its interest for the robotics community as a powerful mathematical tool for dealing with uncertainties.

Jerk Control of Floating Base Systems with Contact-Stable Parametrised Force Feedback

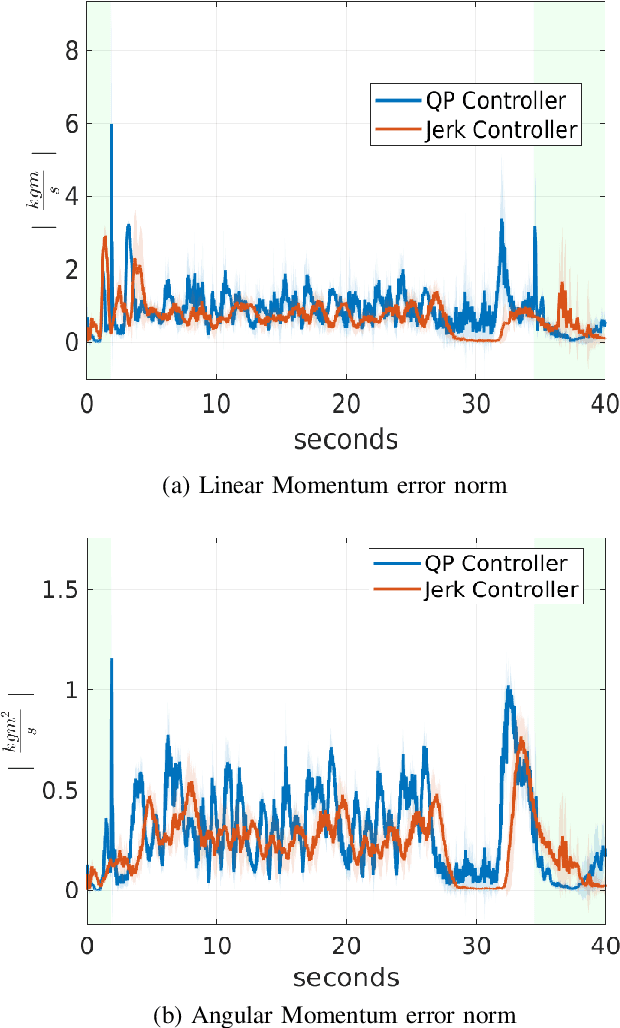
Nonlinear controllers for floating base systems in contact with the environment are often framed as quadratic programming (QP) optimization problems. Common drawbacks of such QP based controllers are: the friction cone constraints are approximated with a set of linear inequalities; the control input often experiences discontinuities; no force feedback from Force/Torque (FT) sensors installed on the robot is taken into account. This paper attempts at addressing these limitations through the design of jerk controllers. These controllers assume the rate-of-change of the joint torques as control input, and exploit the system position, velocity, accelerations, and contact wrenches as measurable quantities. The key ingredient of the presented approach is a one-to-one correspondence between free variables and the manifold defined by the contact stability constraints. This parametrisation allows us to transform the underlying constrained optimisation problems into one that is unconstrained. Then, we propose a jerk control framework that exploits the proposed parametrisation and uses FT measurements in the control loop. Furthermore, we present Lyapunov stable controllers for the system momentum in the jerk control framework. The approach is validated with simulations and experiments using the iCub humanoid robot.