Infinite-Horizon Value Function Approximation for Model Predictive Control

Model Predictive Control has emerged as a popular tool for robots to generate complex motions. However, the real-time requirement has limited the use of hard constraints and large preview horizons, which are necessary to ensure safety and stability. In practice, practitioners have to carefully design cost functions that can imitate an infinite horizon formulation, which is tedious and often results in local minima. In this work, we study how to approximate the infinite horizon value function of constrained optimal control problems with neural networks using value iteration and trajectory optimization. Furthermore, we demonstrate how using this value function approximation as a terminal cost provides global stability to the model predictive controller. The approach is validated on two toy problems and a real-world scenario with online obstacle avoidance on an industrial manipulator where the value function is conditioned to the goal and obstacle.

Nonlinear Stochastic Trajectory Optimization for Centroidal Momentum Motion Generation of Legged Robots

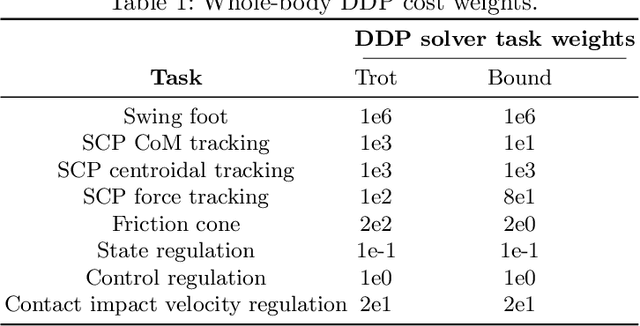
Generation of robust trajectories for legged robots remains a challenging task due to the underlying nonlinear, hybrid and intrinsically unstable dynamics which needs to be stabilized through limited contact forces. Furthermore, disturbances arising from unmodelled contact interactions with the environment and model mismatches can hinder the quality of the planned trajectories leading to unsafe motions. In this work, we propose to use stochastic trajectory optimization for generating robust centroidal momentum trajectories to account for additive uncertainties on the model dynamics and parametric uncertainties on contact locations. Through an alternation between the robust centroidal and whole-body trajectory optimizations, we generate robust momentum trajectories while being consistent with the whole-body dynamics. We perform an extensive set of simulations subject to different uncertainties on a quadruped robot showing that our stochastic trajectory optimization problem reduces the amount of foot slippage for different gaits while achieving better performance over deterministic planning.