Multi-step manipulation task and motion planning guided by video demonstration

This work aims to leverage instructional video to solve complex multi-step task-and-motion planning tasks in robotics. Towards this goal, we propose an extension of the well-established Rapidly-Exploring Random Tree (RRT) planner, which simultaneously grows multiple trees around grasp and release states extracted from the guiding video. Our key novelty lies in combining contact states and 3D object poses extracted from the guiding video with a traditional planning algorithm that allows us to solve tasks with sequential dependencies, for example, if an object needs to be placed at a specific location to be grasped later. We also investigate the generalization capabilities of our approach to go beyond the scene depicted in the instructional video. To demonstrate the benefits of the proposed video-guided planning approach, we design a new benchmark with three challenging tasks: (I) 3D re-arrangement of multiple objects between a table and a shelf, (ii) multi-step transfer of an object through a tunnel, and (iii) transferring objects using a tray similar to a waiter transfers dishes. We demonstrate the effectiveness of our planning algorithm on several robots, including the Franka Emika Panda and the KUKA KMR iiwa. For a seamless transfer of the obtained plans to the real robot, we develop a trajectory refinement approach formulated as an optimal control problem (OCP).

Optimal Control of Walkers with Parallel Actuation

Legged robots with closed-loop kinematic chains are increasingly prevalent due to their increased mobility and efficiency. Yet, most motion generation methods rely on serial-chain approximations, sidestepping their specific constraints and dynamics. This leads to suboptimal motions and limits the adaptability of these methods to diverse kinematic structures. We propose a comprehensive motion generation method that explicitly incorporates closed-loop kinematics and their associated constraints in an optimal control problem, integrating kinematic closure conditions and their analytical derivatives. This allows the solver to leverage the non-linear transmission effects inherent to closed-chain mechanisms, reducing peak actuator efforts and expanding their effective operating range. Unlike previous methods, our framework does not require serial approximations, enabling more accurate and efficient motion strategies. We also are able to generate the motion of more complex robots for which an approximate serial chain does not exist. We validate our approach through simulations and experiments, demonstrating superior performance in complex tasks such as rapid locomotion and stair negotiation. This method enhances the capabilities of current closed-loop robots and broadens the design space for future kinematic architectures.

PhysPose: Refining 6D Object Poses with Physical Constraints

Accurate 6D object pose estimation from images is a key problem in object-centric scene understanding, enabling applications in robotics, augmented reality, and scene reconstruction. Despite recent advances, existing methods often produce physically inconsistent pose estimates, hindering their deployment in real-world scenarios. We introduce PhysPose, a novel approach that integrates physical reasoning into pose estimation through a postprocessing optimization enforcing non-penetration and gravitational constraints. By leveraging scene geometry, PhysPose refines pose estimates to ensure physical plausibility. Our approach achieves state-of-the-art accuracy on the YCB-Video dataset from the BOP benchmark and improves over the state-of-the-art pose estimation methods on the HOPE-Video dataset. Furthermore, we demonstrate its impact in robotics by significantly improving success rates in a challenging pick-and-place task, highlighting the importance of physical consistency in real-world applications.

Infinite-Horizon Value Function Approximation for Model Predictive Control

Model Predictive Control has emerged as a popular tool for robots to generate complex motions. However, the real-time requirement has limited the use of hard constraints and large preview horizons, which are necessary to ensure safety and stability. In practice, practitioners have to carefully design cost functions that can imitate an infinite horizon formulation, which is tedious and often results in local minima. In this work, we study how to approximate the infinite horizon value function of constrained optimal control problems with neural networks using value iteration and trajectory optimization. Furthermore, we demonstrate how using this value function approximation as a terminal cost provides global stability to the model predictive controller. The approach is validated on two toy problems and a real-world scenario with online obstacle avoidance on an industrial manipulator where the value function is conditioned to the goal and obstacle.

Differentiable Simulation of Soft Robots with Frictional Contacts

In recent years, soft robotics simulators have evolved to offer various functionalities, including the simulation of different material types (e.g., elastic, hyper-elastic) and actuation methods (e.g., pneumatic, cable-driven, servomotor). These simulators also provide tools for various tasks, such as calibration, design, and control. However, efficiently and accurately computing derivatives within these simulators remains a challenge, particularly in the presence of physical contact interactions. Incorporating these derivatives can, for instance, significantly improve the convergence speed of control methods like reinforcement learning and trajectory optimization, enable gradient-based techniques for design, or facilitate end-to-end machine-learning approaches for model reduction. This paper addresses these challenges by introducing a unified method for computing the derivatives of mechanical equations within the finite element method framework, including contact interactions modeled as a nonlinear complementarity problem. The proposed approach handles both collision and friction phases, accounts for their nonsmooth dynamics, and leverages the sparsity introduced by mesh-based models. Its effectiveness is demonstrated through several examples of controlling and calibrating soft systems.

End-to-End and Highly-Efficient Differentiable Simulation for Robotics

Over the past few years, robotics simulators have largely improved in efficiency and scalability, enabling them to generate years of simulated data in a few hours. Yet, efficiently and accurately computing the simulation derivatives remains an open challenge, with potentially high gains on the convergence speed of reinforcement learning and trajectory optimization algorithms, especially for problems involving physical contact interactions. This paper contributes to this objective by introducing a unified and efficient algorithmic solution for computing the analytical derivatives of robotic simulators. The approach considers both the collision and frictional stages, accounting for their intrinsic nonsmoothness and also exploiting the sparsity induced by the underlying multibody systems. These derivatives have been implemented in C++, and the code will be open-sourced in the Simple simulator. They depict state-of-the-art timings ranging from 5 microseconds for a 7-dof manipulator up to 95 microseconds for 36-dof humanoid, outperforming alternative solutions by a factor of at least 100.

From Compliant to Rigid Contact Simulation: a Unified and Efficient Approach

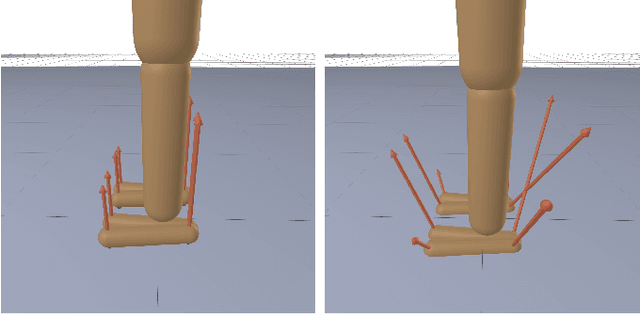
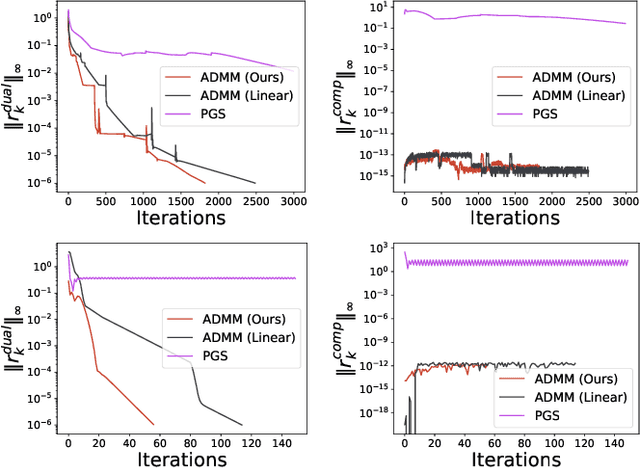
Whether rigid or compliant, contact interactions are inherent to robot motions, enabling them to move or manipulate things. Contact interactions result from complex physical phenomena, that can be mathematically cast as Nonlinear Complementarity Problems (NCPs) in the context of rigid or compliant point contact interactions. Such a class of complementarity problems is, in general, difficult to solve both from an optimization and numerical perspective. Over the past decades, dedicated and specialized contact solvers, implemented in modern robotics simulators (e.g., Bullet, Drake, MuJoCo, DART, Raisim) have emerged. Yet, most of these solvers tend either to solve a relaxed formulation of the original contact problems (at the price of physical inconsistencies) or to scale poorly with the problem dimension or its numerical conditioning (e.g., a robotic hand manipulating a paper sheet). In this paper, we introduce a unified and efficient approach to solving NCPs in the context of contact simulation. It relies on a sound combination of the Alternating Direction Method of Multipliers (ADMM) and proximal algorithms to account for both compliant and rigid contact interfaces in a unified way. To handle ill-conditioned problems and accelerate the convergence rate, we also propose an efficient update strategy to adapt the ADMM hyperparameters automatically. By leveraging proximal methods, we also propose new algorithmic solutions to efficiently evaluate the inverse dynamics involving rigid and compliant contact interactions, extending the approach developed in MuJoCo. We validate the efficiency and robustness of our contact solver against several alternative contact methods of the literature and benchmark them on various robotics and granular mechanics scenarios. Our code is made open-source at https://github.com/Simple-Robotics/Simple.

Parallel and Proximal Linear-Quadratic Methods for Real-Time Constrained Model-Predictive Control

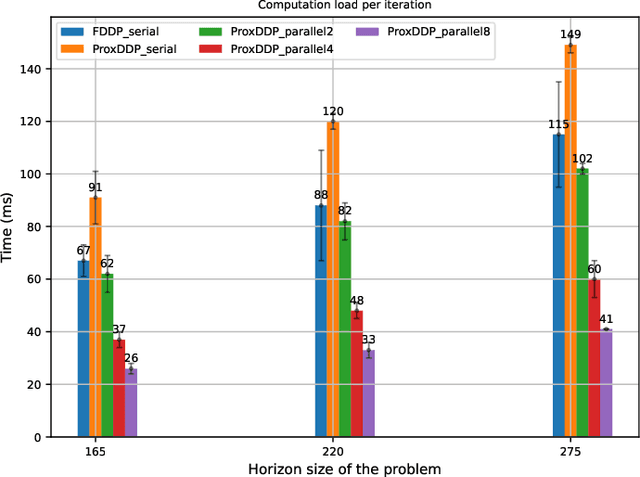
-Recent strides in model predictive control (MPC)underscore a dependence on numerical advancements to efficientlyand accurately solve large-scale problems. Given the substantialnumber of variables characterizing typical whole-body optimalcontrol (OC) problems -often numbering in the thousands-exploiting the sparse structure of the numerical problem becomescrucial to meet computational demands, typically in the range ofa few milliseconds. A fundamental building block for computingNewton or Sequential Quadratic Programming (SQP) steps indirect optimal control methods involves addressing the linearquadratic regulator (LQR) problem. This paper concentrateson equality-constrained problems featuring implicit systemdynamics and dual regularization, a characteristic found inadvanced interior-point or augmented Lagrangian solvers. Here,we introduce a parallel algorithm designed for solving an LQRproblem with dual regularization. Leveraging a rewriting of theLQR recursion through block elimination, we first enhanced theefficiency of the serial algorithm, then subsequently generalized itto handle parametric problems. This extension enables us to splitdecision variables and solve multiple subproblems concurrently.Our algorithm is implemented in our nonlinear numerical optimalcontrol library ALIGATOR. It showcases improved performanceover previous serial formulations and we validate its efficacy bydeploying it in the model predictive control of a real quadrupedrobot. This paper follows up from our prior work on augmentedLagrangian methods for numerical optimal control with implicitdynamics and constraints.

CACTO-SL: Using Sobolev Learning to improve Continuous Actor-Critic with Trajectory Optimization

Trajectory Optimization (TO) and Reinforcement Learning (RL) are powerful and complementary tools to solve optimal control problems. On the one hand, TO can efficiently compute locally-optimal solutions, but it tends to get stuck in local minima if the problem is not convex. On the other hand, RL is typically less sensitive to non-convexity, but it requires a much higher computational effort. Recently, we have proposed CACTO (Continuous Actor-Critic with Trajectory Optimization), an algorithm that uses TO to guide the exploration of an actor-critic RL algorithm. In turns, the policy encoded by the actor is used to warm-start TO, closing the loop between TO and RL. In this work, we present an extension of CACTO exploiting the idea of Sobolev learning. To make the training of the critic network faster and more data efficient, we enrich it with the gradient of the Value function, computed via a backward pass of the differential dynamic programming algorithm. Our results show that the new algorithm is more efficient than the original CACTO, reducing the number of TO episodes by a factor ranging from 3 to 10, and consequently the computation time. Moreover, we show that CACTO-SL helps TO to find better minima and to produce more consistent results.

Risk-Sensitive Extended Kalman Filter

In robotics, designing robust algorithms in the face of estimation uncertainty is a challenging task. Indeed, controllers often do not consider the estimation uncertainty and only rely on the most likely estimated state. Consequently, sudden changes in the environment or the robot's dynamics can lead to catastrophic behaviors. In this work, we present a risk-sensitive Extended Kalman Filter that allows doing output-feedback Model Predictive Control (MPC) safely. This filter adapts its estimation to the control objective. By taking a pessimistic estimate concerning the value function resulting from the MPC controller, the filter provides increased robustness to the controller in phases of uncertainty as compared to a standard Extended Kalman Filter (EKF). Moreover, the filter has the same complexity as an EKF, so that it can be used for real-time model-predictive control. The paper evaluates the risk-sensitive behavior of the proposed filter when used in a nonlinear model-predictive control loop on a planar drone and industrial manipulator in simulation, as well as on an external force estimation task on a real quadruped robot. These experiments demonstrate the abilities of the approach to improve performance in the face of uncertainties significantly.