End-to-End and Highly-Efficient Differentiable Simulation for Robotics

Over the past few years, robotics simulators have largely improved in efficiency and scalability, enabling them to generate years of simulated data in a few hours. Yet, efficiently and accurately computing the simulation derivatives remains an open challenge, with potentially high gains on the convergence speed of reinforcement learning and trajectory optimization algorithms, especially for problems involving physical contact interactions. This paper contributes to this objective by introducing a unified and efficient algorithmic solution for computing the analytical derivatives of robotic simulators. The approach considers both the collision and frictional stages, accounting for their intrinsic nonsmoothness and also exploiting the sparsity induced by the underlying multibody systems. These derivatives have been implemented in C++, and the code will be open-sourced in the Simple simulator. They depict state-of-the-art timings ranging from 5 microseconds for a 7-dof manipulator up to 95 microseconds for 36-dof humanoid, outperforming alternative solutions by a factor of at least 100.

A minimum swept-volume metric structure for configuration space

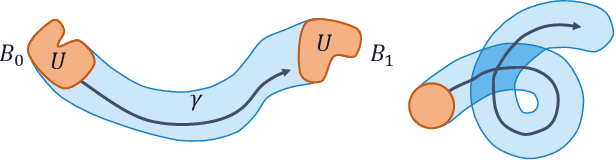
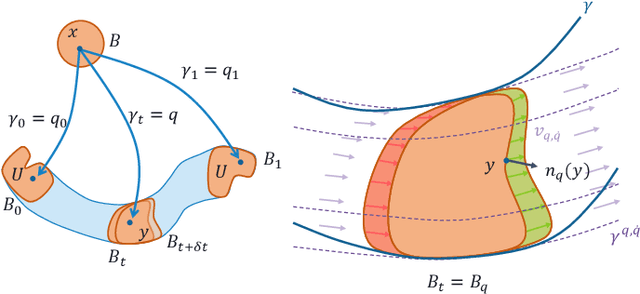
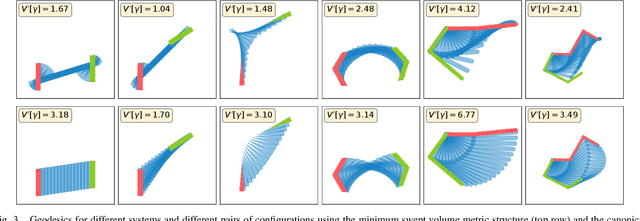
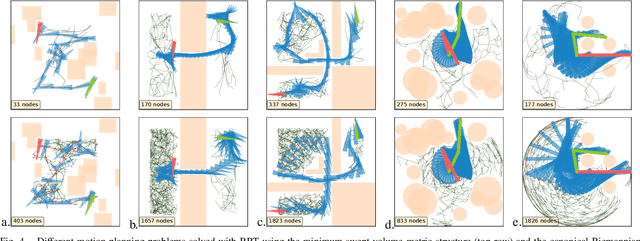
Borrowing elementary ideas from solid mechanics and differential geometry, this presentation shows that the volume swept by a regular solid undergoing a wide class of volume-preserving deformations induces a rather natural metric structure with well-defined and computable geodesics on its configuration space. This general result applies to concrete classes of articulated objects such as robot manipulators, and we demonstrate as a proof of concept the computation of geodesic paths for a free flying rod and planar robotic arms as well as their use in path planning with many obstacles.

Spherical Perspective on Learning with Batch Norm

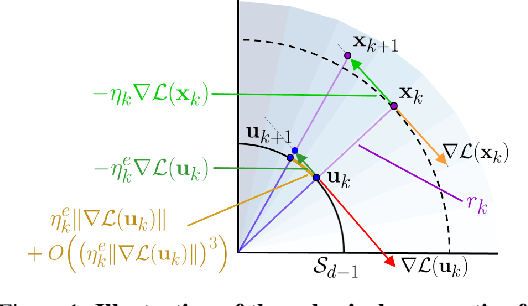
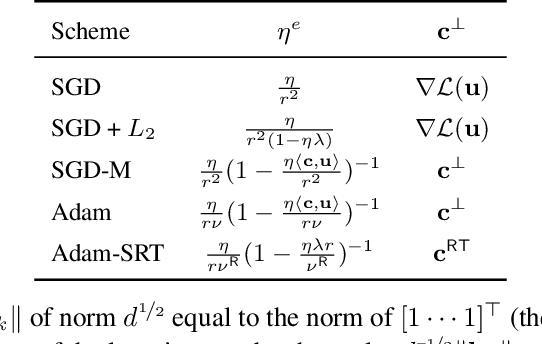
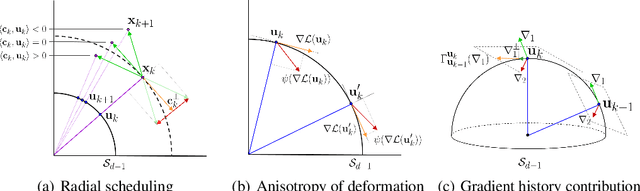
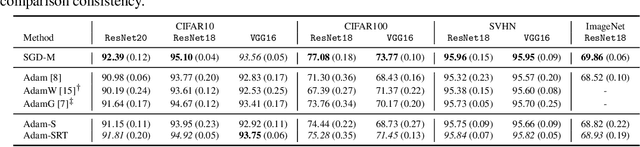
Batch Normalization (BN) is a prominent deep learning technique. In spite of its apparent simplicity, its implications over optimization are yet to be fully understood. In this paper, we study the optimization of neural networks with BN layers from a geometric perspective. We leverage the radial invariance of groups of parameters, such as neurons for multi-layer perceptrons or filters for convolutional neural networks, and translate several popular optimization schemes on the $L_2$ unit hypersphere. This formulation and the associated geometric interpretation sheds new light on the training dynamics and the relation between different optimization schemes. In particular, we use it to derive the effective learning rate of Adam and stochastic gradient descent (SGD) with momentum, and we show that in the presence of BN layers, performing SGD alone is actually equivalent to a variant of Adam constrained to the unit hypersphere. Our analysis also leads us to introduce new variants of Adam. We empirically show, over a variety of datasets and architectures, that they improve accuracy in classification tasks. The complete source code for our experiments is available at: https://github.com/ymontmarin/adamsrt