End-to-End and Highly-Efficient Differentiable Simulation for Robotics

Over the past few years, robotics simulators have largely improved in efficiency and scalability, enabling them to generate years of simulated data in a few hours. Yet, efficiently and accurately computing the simulation derivatives remains an open challenge, with potentially high gains on the convergence speed of reinforcement learning and trajectory optimization algorithms, especially for problems involving physical contact interactions. This paper contributes to this objective by introducing a unified and efficient algorithmic solution for computing the analytical derivatives of robotic simulators. The approach considers both the collision and frictional stages, accounting for their intrinsic nonsmoothness and also exploiting the sparsity induced by the underlying multibody systems. These derivatives have been implemented in C++, and the code will be open-sourced in the Simple simulator. They depict state-of-the-art timings ranging from 5 microseconds for a 7-dof manipulator up to 95 microseconds for 36-dof humanoid, outperforming alternative solutions by a factor of at least 100.

From Compliant to Rigid Contact Simulation: a Unified and Efficient Approach

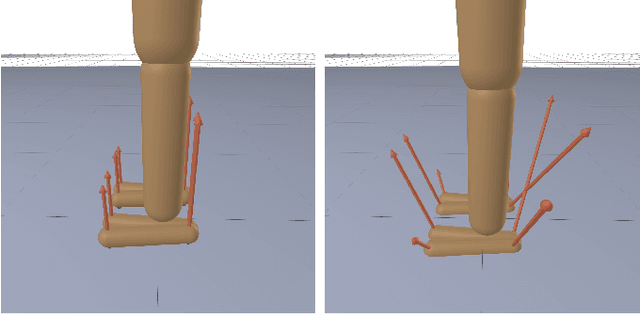
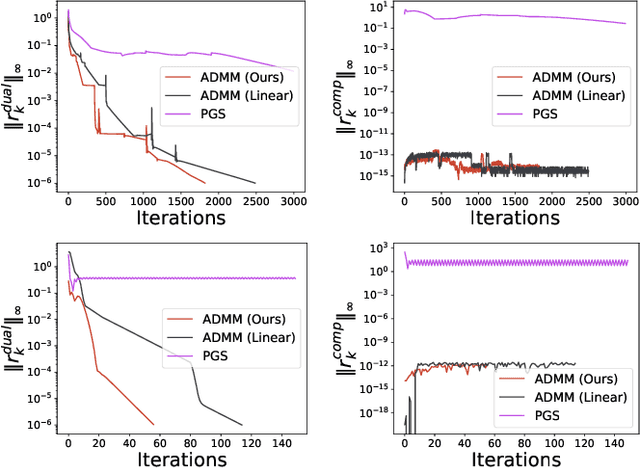
Whether rigid or compliant, contact interactions are inherent to robot motions, enabling them to move or manipulate things. Contact interactions result from complex physical phenomena, that can be mathematically cast as Nonlinear Complementarity Problems (NCPs) in the context of rigid or compliant point contact interactions. Such a class of complementarity problems is, in general, difficult to solve both from an optimization and numerical perspective. Over the past decades, dedicated and specialized contact solvers, implemented in modern robotics simulators (e.g., Bullet, Drake, MuJoCo, DART, Raisim) have emerged. Yet, most of these solvers tend either to solve a relaxed formulation of the original contact problems (at the price of physical inconsistencies) or to scale poorly with the problem dimension or its numerical conditioning (e.g., a robotic hand manipulating a paper sheet). In this paper, we introduce a unified and efficient approach to solving NCPs in the context of contact simulation. It relies on a sound combination of the Alternating Direction Method of Multipliers (ADMM) and proximal algorithms to account for both compliant and rigid contact interfaces in a unified way. To handle ill-conditioned problems and accelerate the convergence rate, we also propose an efficient update strategy to adapt the ADMM hyperparameters automatically. By leveraging proximal methods, we also propose new algorithmic solutions to efficiently evaluate the inverse dynamics involving rigid and compliant contact interactions, extending the approach developed in MuJoCo. We validate the efficiency and robustness of our contact solver against several alternative contact methods of the literature and benchmark them on various robotics and granular mechanics scenarios. Our code is made open-source at https://github.com/Simple-Robotics/Simple.

Contact Models in Robotics: a Comparative Analysis

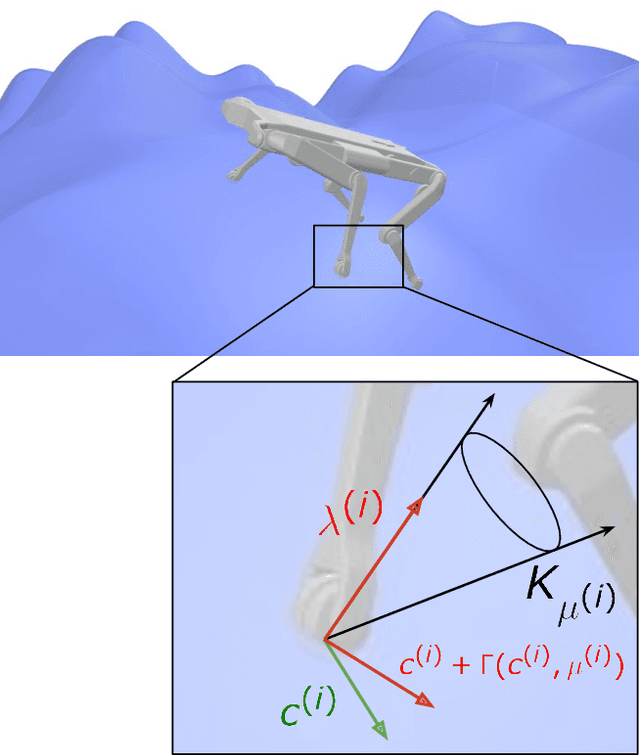
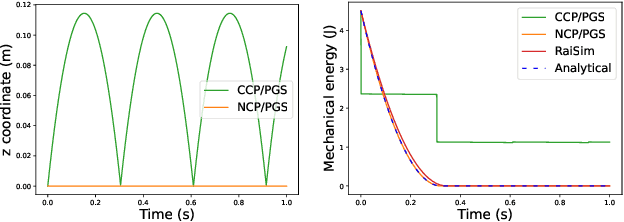
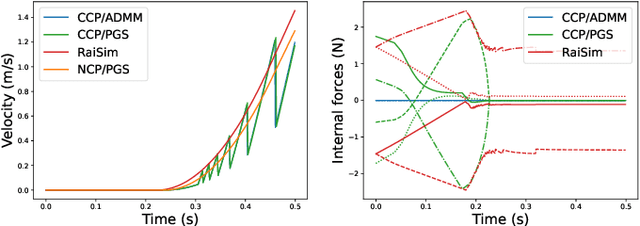
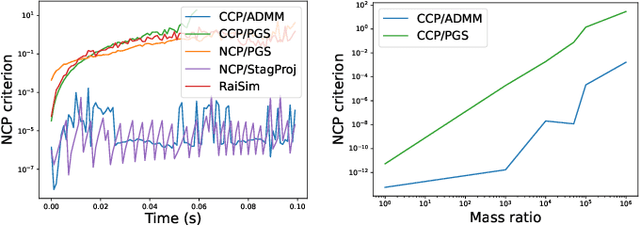
Physics simulation is ubiquitous in robotics. Whether in model-based approaches (e.g., trajectory optimization), or model-free algorithms (e.g., reinforcement learning), physics simulators are a central component of modern control pipelines in robotics. Over the past decades, several robotic simulators have been developed, each with dedicated contact modeling assumptions and algorithmic solutions. In this article, we survey the main contact models and the associated numerical methods commonly used in robotics for simulating advanced robot motions involving contact interactions. In particular, we recall the physical laws underlying contacts and friction (i.e., Signorini condition, Coulomb's law, and the maximum dissipation principle), and how they are transcribed in current simulators. For each physics engine, we expose their inherent physical relaxations along with their limitations due to the numerical techniques employed. Based on our study, we propose theoretically grounded quantitative criteria on which we build benchmarks assessing both the physical and computational aspects of simulation. We support our work with an open-source and efficient C++ implementation of the existing algorithmic variations. Our results demonstrate that some approximations or algorithms commonly used in robotics can severely widen the reality gap and impact target applications. We hope this work will help motivate the development of new contact models, contact solvers, and robotic simulators in general, at the root of recent progress in motion generation in robotics.

Differentiable Collision Detection: a Randomized Smoothing Approach

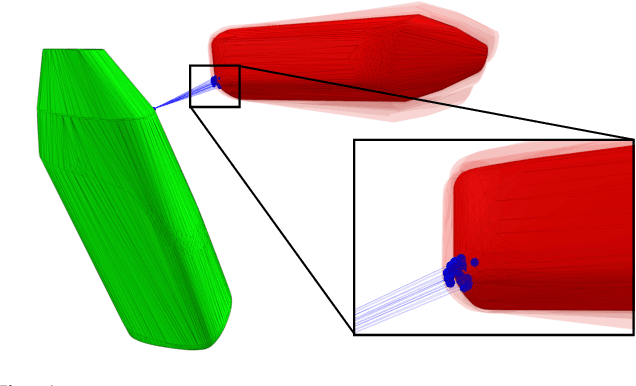
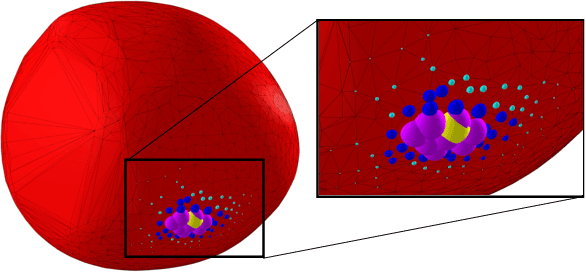
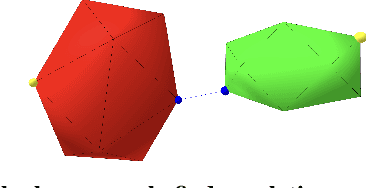
Collision detection appears as a canonical operation in a large range of robotics applications from robot control to simulation, including motion planning and estimation. While the seminal works on the topic date back to the 80s, it is only recently that the question of properly differentiating collision detection has emerged as a central issue, thanks notably to the ongoing and various efforts made by the scientific community around the topic of differentiable physics. Yet, very few solutions have been suggested so far, and only with a strong assumption on the nature of the shapes involved. In this work, we introduce a generic and efficient approach to compute the derivatives of collision detection for any pair of convex shapes, by notably leveraging randomized smoothing techniques which have shown to be particularly adapted to capture the derivatives of non-smooth problems. This approach is implemented in the HPP-FCL and Pinocchio ecosystems, and evaluated on classic datasets and problems of the robotics literature, demonstrating few micro-second timings to compute informative derivatives directly exploitable by many real robotic applications including differentiable simulation.

Augmenting differentiable physics with randomized smoothing

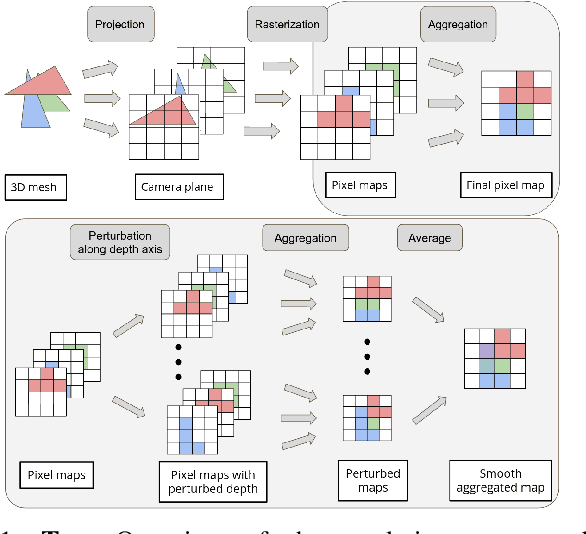
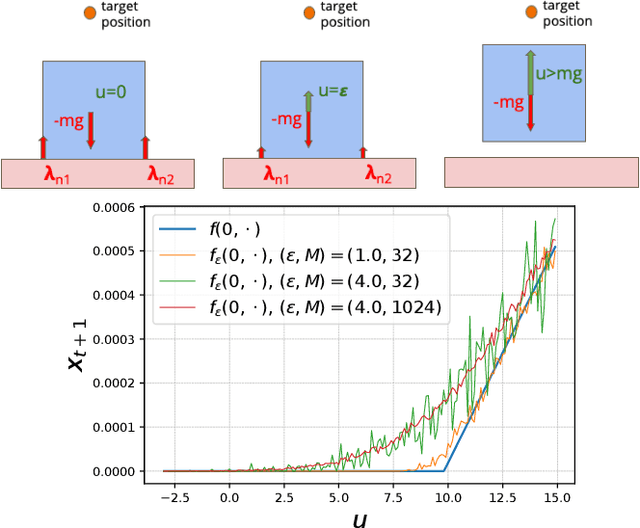
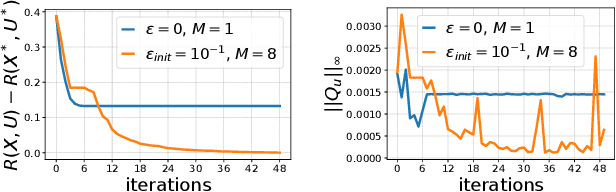
In the past few years, following the differentiable programming paradigm, there has been a growing interest in computing the gradient information of physical processes (e.g., physical simulation, image rendering). However, such processes may be non-differentiable or yield uninformative gradients (i.d., null almost everywhere). When faced with the former pitfalls, gradients estimated via analytical expression or numerical techniques such as automatic differentiation and finite differences, make classical optimization schemes converge towards poor quality solutions. Thus, relying only on the local information provided by these gradients is often not sufficient to solve advanced optimization problems involving such physical processes, notably when they are subject to non-smoothness and non-convexity issues.In this work, inspired by the field of zero-th order optimization, we leverage randomized smoothing to augment differentiable physics by estimating gradients in a neighborhood. Our experiments suggest that integrating this approach inside optimization algorithms may be fruitful for tasks as varied as mesh reconstruction from images or optimal control of robotic systems subject to contact and friction issues.

Collision Detection Accelerated: An Optimization Perspective

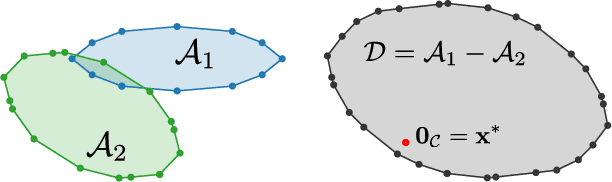
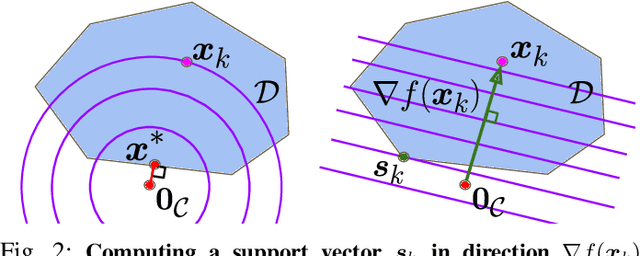
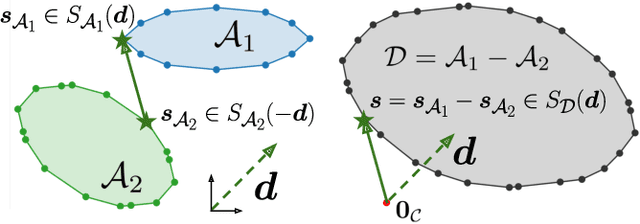
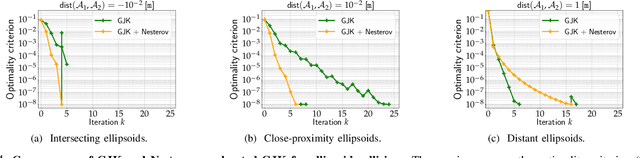
Collision detection between two convex shapes is an essential feature of any physics engine or robot motion planner. It has often been tackled as a computational geometry problem, with the Gilbert, Johnson and Keerthi (GJK) algorithm being the most common approach today. In this work we leverage the fact that collision detection is fundamentally a convex optimization problem. In particular, we establish that the GJK algorithm is a specific sub-case of the well-established Frank-Wolfe (FW) algorithm in convex optimization. We introduce a new collision detection algorithm by adapting recent works linking Nesterov acceleration and Frank-Wolfe methods. We benchmark the proposed accelerated collision detection method on two datasets composed of strictly convex and non-strictly convex shapes. Our results show that our approach significantly reduces the number of iterations to solve collision detection problems compared to the state-of-the-art GJK algorithm, leading to up to two times faster computation times.

Leveraging Randomized Smoothing for Optimal Control of Nonsmooth Dynamical Systems

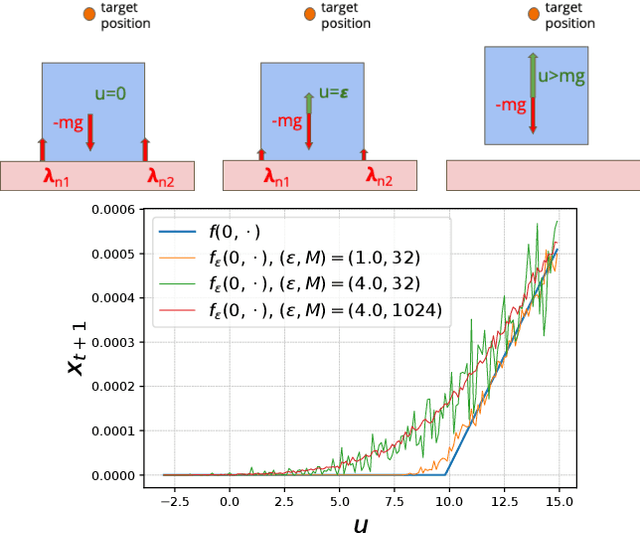
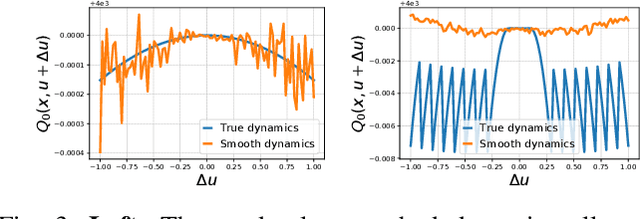
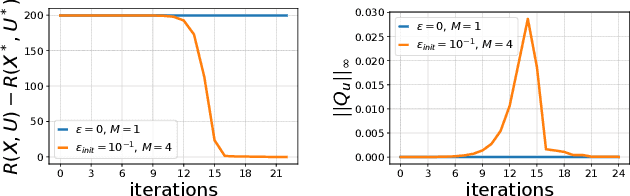
Optimal control (OC) algorithms such as Differential Dynamic Programming (DDP) take advantage of the derivatives of the dynamics to efficiently control physical systems. Yet, in the presence of nonsmooth dynamical systems, such class of algorithms are likely to fail due, for instance, to the presence of discontinuities in the dynamics derivatives or because of non-informative gradient. On the contrary, reinforcement learning (RL) algorithms have shown better empirical results in scenarios exhibiting non-smooth effects (contacts, frictions, etc). Our approach leverages recent works on randomized smoothing (RS) to tackle non-smoothness issues commonly encountered in optimal control, and provides key insights on the interplay between RL and OC through the prism of RS methods. This naturally leads us to introduce the randomized Differential Dynamic Programming (R-DDP) algorithm accounting for deterministic but non-smooth dynamics in a very sample-efficient way. The experiments demonstrate that our method is able to solve classic robotic problems with dry friction and frictional contacts, where classical OC algorithms are likely to fail and RL algorithms require in practice a prohibitive number of samples to find an optimal solution.