PhysPose: Refining 6D Object Poses with Physical Constraints

Accurate 6D object pose estimation from images is a key problem in object-centric scene understanding, enabling applications in robotics, augmented reality, and scene reconstruction. Despite recent advances, existing methods often produce physically inconsistent pose estimates, hindering their deployment in real-world scenarios. We introduce PhysPose, a novel approach that integrates physical reasoning into pose estimation through a postprocessing optimization enforcing non-penetration and gravitational constraints. By leveraging scene geometry, PhysPose refines pose estimates to ensure physical plausibility. Our approach achieves state-of-the-art accuracy on the YCB-Video dataset from the BOP benchmark and improves over the state-of-the-art pose estimation methods on the HOPE-Video dataset. Furthermore, we demonstrate its impact in robotics by significantly improving success rates in a challenging pick-and-place task, highlighting the importance of physical consistency in real-world applications.

6D Object Pose Tracking in Internet Videos for Robotic Manipulation

We seek to extract a temporally consistent 6D pose trajectory of a manipulated object from an Internet instructional video. This is a challenging set-up for current 6D pose estimation methods due to uncontrolled capturing conditions, subtle but dynamic object motions, and the fact that the exact mesh of the manipulated object is not known. To address these challenges, we present the following contributions. First, we develop a new method that estimates the 6D pose of any object in the input image without prior knowledge of the object itself. The method proceeds by (i) retrieving a CAD model similar to the depicted object from a large-scale model database, (ii) 6D aligning the retrieved CAD model with the input image, and (iii) grounding the absolute scale of the object with respect to the scene. Second, we extract smooth 6D object trajectories from Internet videos by carefully tracking the detected objects across video frames. The extracted object trajectories are then retargeted via trajectory optimization into the configuration space of a robotic manipulator. Third, we thoroughly evaluate and ablate our 6D pose estimation method on YCB-V and HOPE-Video datasets as well as a new dataset of instructional videos manually annotated with approximate 6D object trajectories. We demonstrate significant improvements over existing state-of-the-art RGB 6D pose estimation methods. Finally, we show that the 6D object motion estimated from Internet videos can be transferred to a 7-axis robotic manipulator both in a virtual simulator as well as in a real world set-up. We also successfully apply our method to egocentric videos taken from the EPIC-KITCHENS dataset, demonstrating potential for Embodied AI applications.

Visually Guided Model Predictive Robot Control via 6D Object Pose Localization and Tracking

The objective of this work is to enable manipulation tasks with respect to the 6D pose of a dynamically moving object using a camera mounted on a robot. Examples include maintaining a constant relative 6D pose of the robot arm with respect to the object, grasping the dynamically moving object, or co-manipulating the object together with a human. Fast and accurate 6D pose estimation is crucial to achieve smooth and stable robot control in such situations. The contributions of this work are three fold. First, we propose a new visual perception module that asynchronously combines accurate learning-based 6D object pose localizer and a high-rate model-based 6D pose tracker. The outcome is a low-latency accurate and temporally consistent 6D object pose estimation from the input video stream at up to 120 Hz. Second, we develop a visually guided robot arm controller that combines the new visual perception module with a torque-based model predictive control algorithm. Asynchronous combination of the visual and robot proprioception signals at their corresponding frequencies results in stable and robust 6D object pose guided robot arm control. Third, we experimentally validate the proposed approach on a challenging 6D pose estimation benchmark and demonstrate 6D object pose-guided control with dynamically moving objects on a real 7 DoF Franka Emika Panda robot.

Differentiable Collision Detection: a Randomized Smoothing Approach

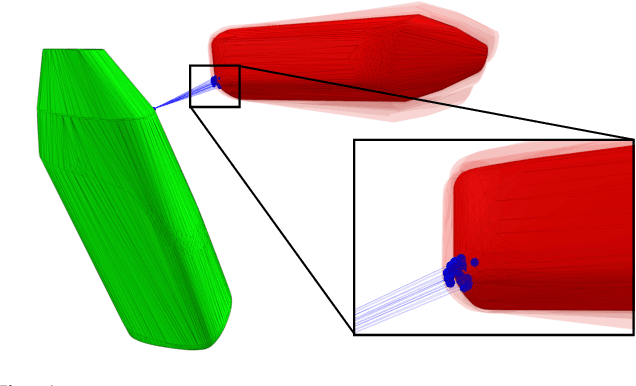
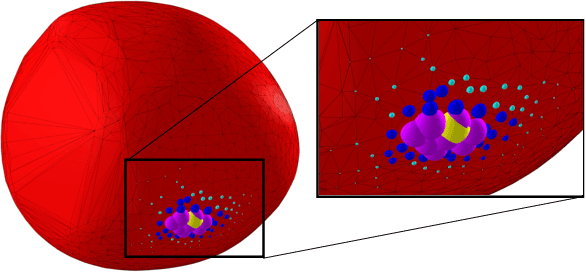
Collision detection appears as a canonical operation in a large range of robotics applications from robot control to simulation, including motion planning and estimation. While the seminal works on the topic date back to the 80s, it is only recently that the question of properly differentiating collision detection has emerged as a central issue, thanks notably to the ongoing and various efforts made by the scientific community around the topic of differentiable physics. Yet, very few solutions have been suggested so far, and only with a strong assumption on the nature of the shapes involved. In this work, we introduce a generic and efficient approach to compute the derivatives of collision detection for any pair of convex shapes, by notably leveraging randomized smoothing techniques which have shown to be particularly adapted to capture the derivatives of non-smooth problems. This approach is implemented in the HPP-FCL and Pinocchio ecosystems, and evaluated on classic datasets and problems of the robotics literature, demonstrating few micro-second timings to compute informative derivatives directly exploitable by many real robotic applications including differentiable simulation.

Learning Object Manipulation Skills from Video via Approximate Differentiable Physics

We aim to teach robots to perform simple object manipulation tasks by watching a single video demonstration. Towards this goal, we propose an optimization approach that outputs a coarse and temporally evolving 3D scene to mimic the action demonstrated in the input video. Similar to previous work, a differentiable renderer ensures perceptual fidelity between the 3D scene and the 2D video. Our key novelty lies in the inclusion of a differentiable approach to solve a set of Ordinary Differential Equations (ODEs) that allows us to approximately model laws of physics such as gravity, friction, and hand-object or object-object interactions. This not only enables us to dramatically improve the quality of estimated hand and object states, but also produces physically admissible trajectories that can be directly translated to a robot without the need for costly reinforcement learning. We evaluate our approach on a 3D reconstruction task that consists of 54 video demonstrations sourced from 9 actions such as pull something from right to left or put something in front of something. Our approach improves over previous state-of-the-art by almost 30%, demonstrating superior quality on especially challenging actions involving physical interactions of two objects such as put something onto something. Finally, we showcase the learned skills on a Franka Emika Panda robot.

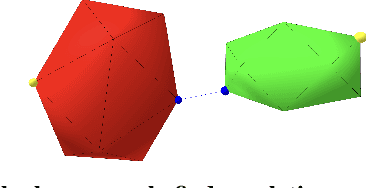
Collision Detection Accelerated: An Optimization Perspective

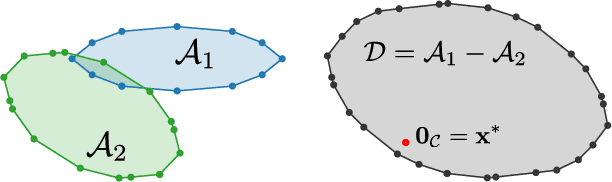
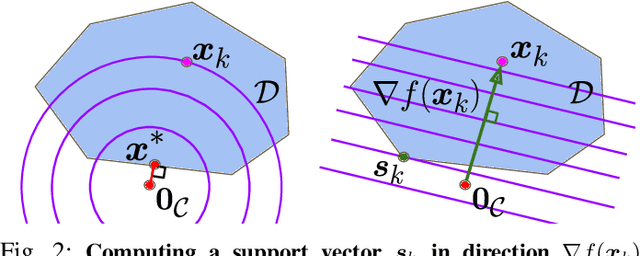
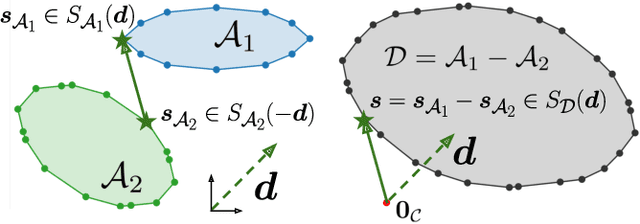
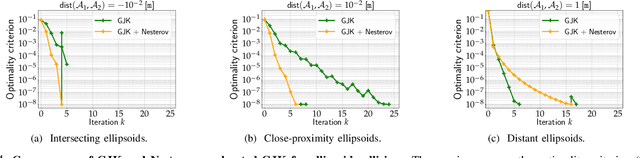
Collision detection between two convex shapes is an essential feature of any physics engine or robot motion planner. It has often been tackled as a computational geometry problem, with the Gilbert, Johnson and Keerthi (GJK) algorithm being the most common approach today. In this work we leverage the fact that collision detection is fundamentally a convex optimization problem. In particular, we establish that the GJK algorithm is a specific sub-case of the well-established Frank-Wolfe (FW) algorithm in convex optimization. We introduce a new collision detection algorithm by adapting recent works linking Nesterov acceleration and Frank-Wolfe methods. We benchmark the proposed accelerated collision detection method on two datasets composed of strictly convex and non-strictly convex shapes. Our results show that our approach significantly reduces the number of iterations to solve collision detection problems compared to the state-of-the-art GJK algorithm, leading to up to two times faster computation times.