Constrained Differential Dynamic Programming: A primal-dual augmented Lagrangian approach

Trajectory optimization is an efficient approach for solving optimal control problems for complex robotic systems. It relies on two key components: first the transcription into a sparse nonlinear program, and second the corresponding solver to iteratively compute its solution. On one hand, differential dynamic programming (DDP) provides an efficient approach to transcribe the optimal control problem into a finite-dimensional problem while optimally exploiting the sparsity induced by time. On the other hand, augmented Lagrangian methods make it possible to formulate efficient algorithms with advanced constraint-satisfaction strategies. In this paper, we propose to combine these two approaches into an efficient optimal control algorithm accepting both equality and inequality constraints. Based on the augmented Lagrangian literature, we first derive a generic primal-dual augmented Lagrangian strategy for nonlinear problems with equality and inequality constraints. We then apply it to the dynamic programming principle to solve the value-greedy optimization problems inherent to the backward pass of DDP, which we combine with a dedicated globalization strategy, resulting in a Newton-like algorithm for solving constrained trajectory optimization problems. Contrary to previous attempts of formulating an augmented Lagrangian version of DDP, our approach exhibits adequate convergence properties without any switch in strategies. We empirically demonstrate its interest with several case-studies from the robotics literature.

ProxNLP: a primal-dual augmented Lagrangian solver for nonlinear programming in Robotics and beyond

Mathematical optimization is the workhorse behind several aspects of modern robotics and control. In these applications, the focus is on constrained optimization, and the ability to work on manifolds (such as the classical matrix Lie groups), along with a specific requirement for robustness and speed. In recent years, augmented Lagrangian methods have seen a resurgence due to their robustness and flexibility, their connections to (inexact) proximal-point methods, and their interoperability with Newton or semismooth Newton methods. In the sequel, we present primal-dual augmented Lagrangian method for inequality-constrained problems on manifolds, which we introduced in our recent work, as well as an efficient C++ implementation suitable for use in robotics applications and beyond.

Differentiable Collision Detection: a Randomized Smoothing Approach

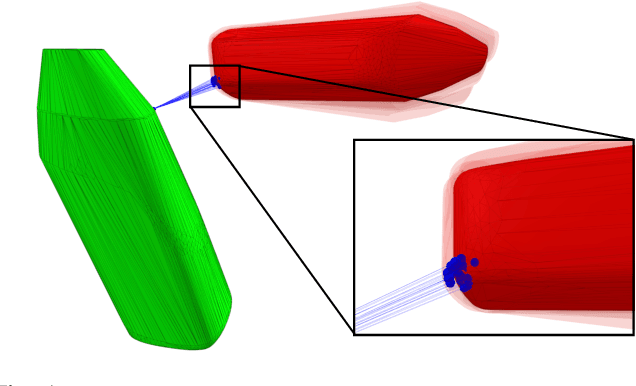
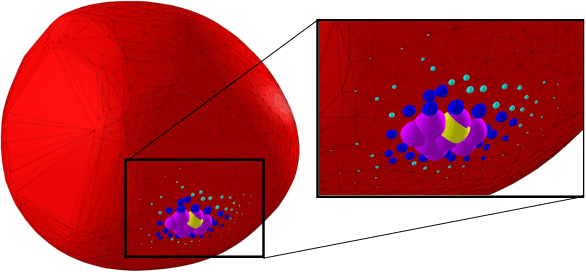
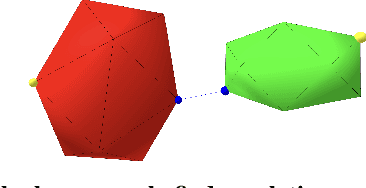
Collision detection appears as a canonical operation in a large range of robotics applications from robot control to simulation, including motion planning and estimation. While the seminal works on the topic date back to the 80s, it is only recently that the question of properly differentiating collision detection has emerged as a central issue, thanks notably to the ongoing and various efforts made by the scientific community around the topic of differentiable physics. Yet, very few solutions have been suggested so far, and only with a strong assumption on the nature of the shapes involved. In this work, we introduce a generic and efficient approach to compute the derivatives of collision detection for any pair of convex shapes, by notably leveraging randomized smoothing techniques which have shown to be particularly adapted to capture the derivatives of non-smooth problems. This approach is implemented in the HPP-FCL and Pinocchio ecosystems, and evaluated on classic datasets and problems of the robotics literature, demonstrating few micro-second timings to compute informative derivatives directly exploitable by many real robotic applications including differentiable simulation.