Collision Detection Accelerated: An Optimization Perspective
Paper and Code
May 20, 2022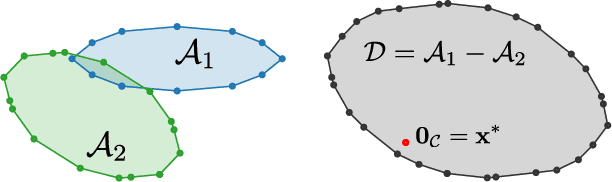
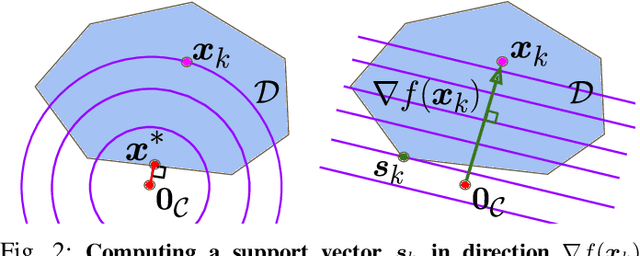
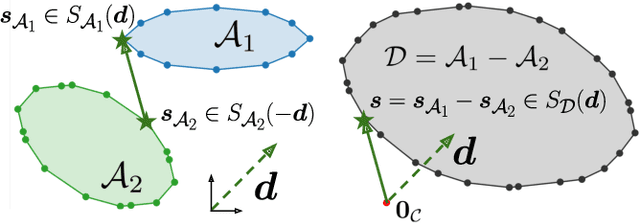
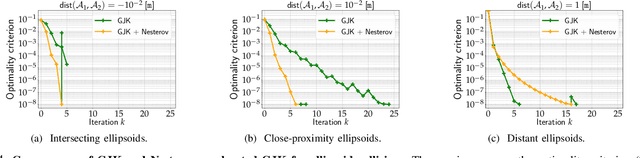
Collision detection between two convex shapes is an essential feature of any physics engine or robot motion planner. It has often been tackled as a computational geometry problem, with the Gilbert, Johnson and Keerthi (GJK) algorithm being the most common approach today. In this work we leverage the fact that collision detection is fundamentally a convex optimization problem. In particular, we establish that the GJK algorithm is a specific sub-case of the well-established Frank-Wolfe (FW) algorithm in convex optimization. We introduce a new collision detection algorithm by adapting recent works linking Nesterov acceleration and Frank-Wolfe methods. We benchmark the proposed accelerated collision detection method on two datasets composed of strictly convex and non-strictly convex shapes. Our results show that our approach significantly reduces the number of iterations to solve collision detection problems compared to the state-of-the-art GJK algorithm, leading to up to two times faster computation times.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge