Take One Gram of Neural Features, Get Enhanced Group Robustness

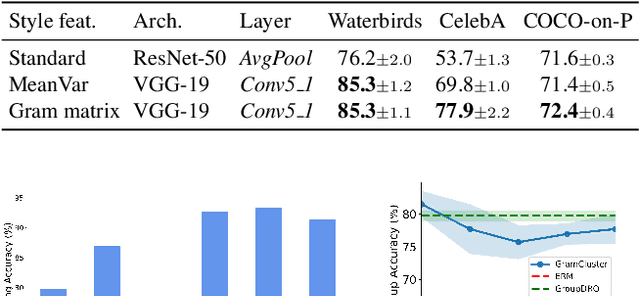
Predictive performance of machine learning models trained with empirical risk minimization (ERM) can degrade considerably under distribution shifts. The presence of spurious correlations in training datasets leads ERM-trained models to display high loss when evaluated on minority groups not presenting such correlations. Extensive attempts have been made to develop methods improving worst-group robustness. However, they require group information for each training input or at least, a validation set with group labels to tune their hyperparameters, which may be expensive to get or unknown a priori. In this paper, we address the challenge of improving group robustness without group annotation during training or validation. To this end, we propose to partition the training dataset into groups based on Gram matrices of features extracted by an ``identification'' model and to apply robust optimization based on these pseudo-groups. In the realistic context where no group labels are available, our experiments show that our approach not only improves group robustness over ERM but also outperforms all recent baselines

Localizing Objects with Self-Supervised Transformers and no Labels

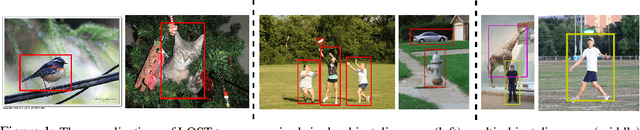
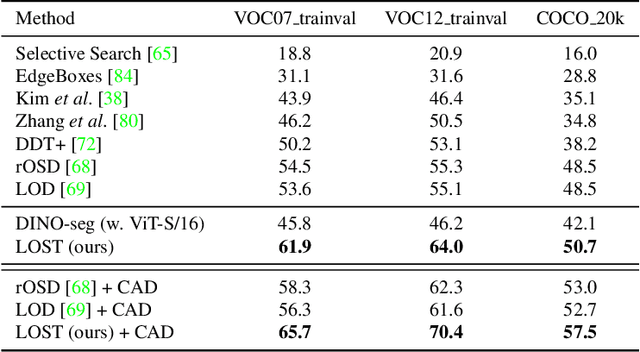
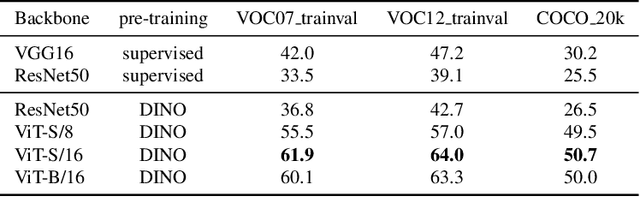
Localizing objects in image collections without supervision can help to avoid expensive annotation campaigns. We propose a simple approach to this problem, that leverages the activation features of a vision transformer pre-trained in a self-supervised manner. Our method, LOST, does not require any external object proposal nor any exploration of the image collection; it operates on a single image. Yet, we outperform state-of-the-art object discovery methods by up to 8 CorLoc points on PASCAL VOC 2012. We also show that training a class-agnostic detector on the discovered objects boosts results by another 7 points. Moreover, we show promising results on the unsupervised object discovery task. The code to reproduce our results can be found at https://github.com/valeoai/LOST.

Spherical Perspective on Learning with Batch Norm

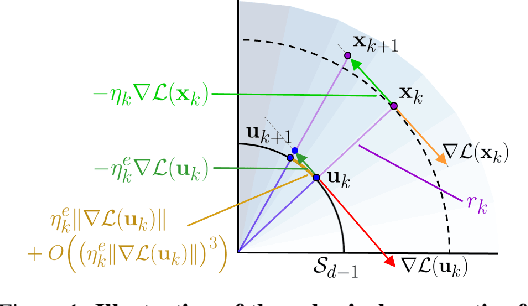
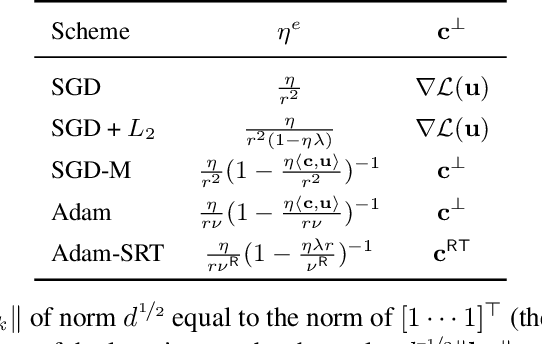
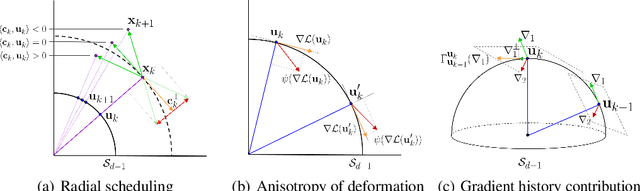
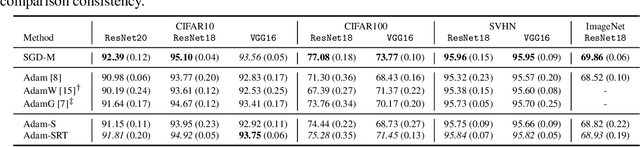
Batch Normalization (BN) is a prominent deep learning technique. In spite of its apparent simplicity, its implications over optimization are yet to be fully understood. In this paper, we study the optimization of neural networks with BN layers from a geometric perspective. We leverage the radial invariance of groups of parameters, such as neurons for multi-layer perceptrons or filters for convolutional neural networks, and translate several popular optimization schemes on the $L_2$ unit hypersphere. This formulation and the associated geometric interpretation sheds new light on the training dynamics and the relation between different optimization schemes. In particular, we use it to derive the effective learning rate of Adam and stochastic gradient descent (SGD) with momentum, and we show that in the presence of BN layers, performing SGD alone is actually equivalent to a variant of Adam constrained to the unit hypersphere. Our analysis also leads us to introduce new variants of Adam. We empirically show, over a variety of datasets and architectures, that they improve accuracy in classification tasks. The complete source code for our experiments is available at: https://github.com/ymontmarin/adamsrt